Идемпотентная матрица

На этой странице мы объясняем, что такое идемпотентные матрицы. Мы также покажем вам несколько примеров матриц этого типа, чтобы вы полностью поняли это. Также вы найдете формулу нахождения идемпотентной матрицы и, наконец, все свойства идемпотентных матриц.

Что такое идемпотентная матрица?

Определение идемпотентной матрицы следующее:

Идемпотентная матрица — это та матрица, которая при умножении сама на себя дает в результате одну и ту же матрицу.

$A\cdot A = A$

Следовательно, любая степень идемпотентной матрицы равна самой матрице независимо от показателя степени:

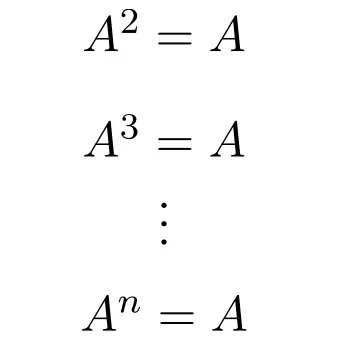
Собственно, именно поэтому этот тип доски и получил свое название. Потому что в математике идемпотентность — это операция, означающая, что мы всегда получаем один и тот же результат, независимо от того, сколько раз она выполняется.

Примеры идемпотентных матриц

Как только мы узнаем концепцию идемпотентной матрицы, мы увидим несколько примеров различных измерений, чтобы завершить ее понимание.

Пример идемпотентной матрицы 2×2

Следующая квадратная матрица размерности 2×2 идемпотентна:

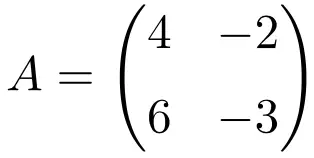
пример идемпотентной матрицы размерности 2x2

Чтобы убедиться, что это идемпотентная матрица, вычислим ее квадрат:

$\displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}$

Результат идентичен, поэтому мы показываем, что это идемпотентная матрица.

Пример идемпотентной матрицы 3×3

Следующая квадратная матрица размером 3×3 является идемпотентной:

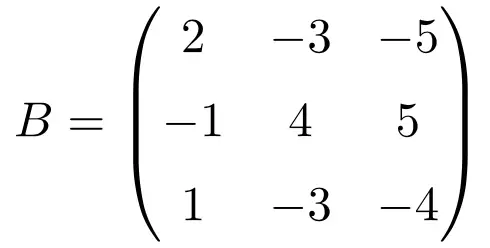
пример идемпотентной матрицы размерности 3x3

Чтобы проверить соответствие идемпотентной матрицы, мы повышаем матрицу до 2:

$\displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}$

Результат тот же, что и исходная матрица, поэтому идемпотентность матрицы доказана.

Структура идемпотентной матрицы 2×2.

Здесь мы покажем вам формулу для получения идемпотентной матрицы. Если вас больше интересует, вы можете увидеть демонстрацию формулы ниже в комментариях, но это немного утомительно, поэтому здесь мы оставляем вам непосредственно формулу для идемпотентных матриц :

Таким образом, элементы вторичной диагонали идемпотентной матрицы могут быть произвольными, пока выполняется условие

$a^2+bc=a$

и числа на главной диагонали должны быть

$a$

$1-a.$

В дополнение ко всем матрицам, описанным этой формулой, мы должны добавить матрицу идентичности, которая также является идемпотентной матрицей, хотя и не учитывает формулу. Если вы не знаете, что это за массив, вы можете спросить, что такое массив Identity .

Свойства идемпотентных матриц

Идемпотентные матрицы обладают следующими характеристиками:

Определитель идемпотентной матрицы всегда равен 0 или 1.

За исключением единичной матрицы, все остальные идемпотентные матрицы являются либо сингулярными, либо вырожденными матрицами, то есть необратимы.

Любая идемпотентная матрица диагонализуема, и ее собственные значения (или собственные значения) всегда равны 0 или 1.

След идемпотентной матрицы равен рангу матрицы.

Наконец, существует связь между идемпотентными и инволюционными матрицами: матрица
$A$

идемпотентна тогда и только тогда, когда матрица

$\displaystyle P= 2A-I$

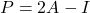
это инволюционно.