В этой статье вы узнаете, как найти арктангенс функции. Кроме того, вы сможете увидеть примеры такого типа производной и даже попрактиковаться с решением упражнений на производную арктангенса. Наконец, мы также покажем вам доказательство формулы для производной арктангенса.
Что является производной арктангенса?
Производная арктангенса x равна единице плюс x в квадрате.
![]()
Следовательно, производная арктангенса функции равна частному производной этой функции, деленному на единицу, плюс квадрат этой функции.
![]()
В данном случае функция была представлена как au, так что это будет формула для производной арктангенса функции u.
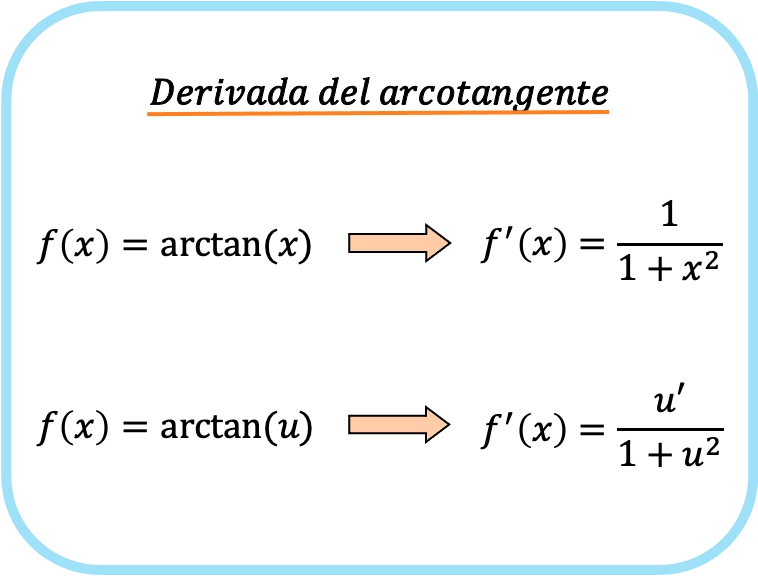
Как видите, формула производной обратного тангенса очень похожа на формулы производных арксинуса и арккосинуса.
Примеры производной арктангенса
Как только мы узнаем формулу производной арктангенса, мы объясним вывод нескольких примеров этого типа тригонометрических производных. Так вам будет легче понять, как получается арктангенс функции.
Пример 1: Производная арктангенса 2x
![]()
Применим формулу для решения производной:
![]()
Производная 2x равна 2, поэтому арктангенс производной 2x равен 2 по единице плюс 2x в квадрате:
![]()
Пример 2: Производная арктангенса x в квадрате
![]()
Чтобы найти результат производной этого примера, нам нужно использовать формулу производной арктангенса, которая имеет вид:
![]()
Таким образом, производная функции x 2 равна 2x, поэтому производная арктангенса x, возведенного в степень 2, равна:
![]()
Пример 3: Производная арктангенса синуса x
![]()
Логично, что для расчета производной необходимо применить соответствующую формулу:
![]()
В данном случае у нас есть составная функция, поэтому мы должны применить цепное правило для вычисления производной арктангенса:
![]()
Решенные упражнения на производную арктангенса
Выведите следующие функции арктангенса:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
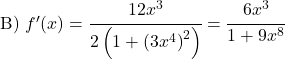
![]()
![]()
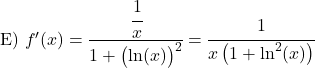
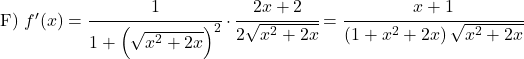
Демонстрация формулы производной арктангенса
Далее мы докажем формулу производной арктангенса.
![]()
Сначала мы преобразуем арктангенс в тангенс, воспользовавшись тем фактом, что арктангенс является обратной функцией тангенса:
![]()
Дифференцируем две части уравнения:
![]()
Стираем и’:
![]()
С другой стороны, благодаря фундаментальному тригонометрическому тождеству мы знаем, что сумма квадратов синуса и косинуса равна 1. Поэтому мы можем преобразовать предыдущее выражение в дробь:
![]()
![]()
Делим все слагаемые на квадрат косинуса:
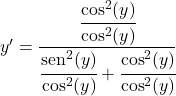
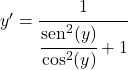
Синус, разделенный на косинус, равен тангенсу, поэтому:
![]()
![]()
Как мы видели выше, тангенс эквивалентен переменной x, поэтому мы можем подставить выражение, чтобы получить формулу для производной арктангенса:
![]()