На этой странице вы увидите, что такое ортогональные матрицы и как они связаны с обратной матрицей. Вы также увидите несколько примеров, чтобы лучше понять это. Кроме того, мы научим вас формуле проверки любой ортогональной матрицы, с помощью которой вы сможете быстро ее найти. И, наконец, вы найдете свойства и применение этих конкретных матриц, а также типичное решение экзаменационного упражнения.
Что такое ортогональная матрица?
Определение ортогональной матрицы следующее:
Ортогональная матрица — это квадратная матрица действительных чисел, умноженная на ее транспонирование (или транспонирование), равна единичной матрице. То есть выполняется следующее условие:
![]()
Золото
![]()
является ортогональной матрицей и
![]()
представляет его транспонированную матрицу.
Чтобы это условие выполнялось, столбцы и строки ортогональной матрицы должны быть ортогональными единичными векторами, то есть они должны образовывать ортонормированный базис. По этой причине некоторые математики также называют их ортонормированными матрицами .
Обратная ортогональная матрица
Другой способ объяснить понятие ортогональной матрицы — через обратную матрицу, поскольку транспонированная (или транспонированная) матрица ортогональной матрицы равна ее обратной.
Чтобы полностью понять эту теорему, важно знать, как инвертировать матрицу . По этой ссылке вы найдете подробное объяснение обратной матрицы, всех ее свойств и даже пошаговые решения упражнений для практики.
Можно легко показать, что обратная матрица ортогональной матрицы эквивалентна ее транспонированию, используя условие ортогональной матрицы и основное свойство обратных матриц:
![Rendered by QuickLaTeX.com \left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36f7666e4730a6311c088c7e8d7f0f38_l3.png)
Следовательно, ортогональная матрица всегда будет обратимой матрицей , или, другими словами, это будет регулярная или невырожденная матрица.
Далее мы увидим несколько примеров ортогональных матриц, чтобы завершить понимание концепции всего.
Пример ортогональной матрицы 2×2
Следующая матрица является ортогональной матрицей размерности 2×2:
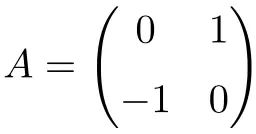
Мы можем проверить, что оно ортогонально, вычислив произведение путем его транспонирования:
![]()
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7baa091c2fd963507b93e6bec5c386b_l3.png)
Поскольку результат дает идентичную матрицу, мы проверяем, что A является ортогональной матрицей.
Пример ортогональной матрицы 3×3
Следующая матрица является ортогональной матрицей размерности 3×3:
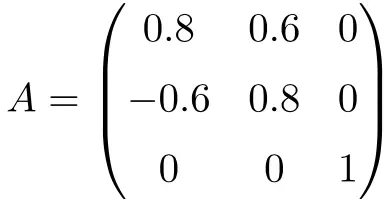
Мы можем показать, что она ортогональна, умножив матрицу A на ее транспонирование:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-35687f56ff4ad5d1b19ea673b4ac85de_l3.png)
Поскольку решением является унитарная матрица, мы покажем, что A — ортогональная матрица.
Формула нахождения ортогональной матрицы 2×2
Затем мы увидим доказательство того, что все ортогональные матрицы порядка 2 следуют одному и тому же шаблону.
Рассмотрим общую матрицу размера 2×2:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac19d6ab63d390a9340cbce4014b1136_l3.png)
Чтобы эта матрица была ортогональной, должно выполняться следующее матричное уравнение:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e108701513ef6f2118e3b7d32657cd8_l3.png)
Решая умножение матриц, получаем следующие уравнения:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d5435c614cb0da442fe04f65aec89637_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8897132ecdbf389450e8c5fa1707226_l3.png)
Если присмотреться, эти равенства очень похожи на фундаментальное тригонометрическое соотношение Пифагора :
![]()
Следовательно, членами, удовлетворяющими полученным уравнениям (1) и (3), являются:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9abeb023c5050d8d7f6fbab8c52227ba_l3.png)
Дополнительно, подставив значения во второе уравнение, получим связь между двумя углами:
![]()
![]()
![]()
То есть должно быть выполнено одно из следующих двух условий:
![]()
![]()
Итак, в заключение, ортогональные матрицы должны иметь структуру одной из следующих двух матриц:

Золото
![]()
это действительное число.
Действительно, если в качестве примера мы присвоим значение
![]()
и возьмем первую структуру, мы получим матрицу, ортогональность которой мы проверили в разделе «Пример ортогональной матрицы 2 × 2»:
![Rendered by QuickLaTeX.com \displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1a331cab64745933f7c8a5009c799be6_l3.png)
Свойства ортогональной матрицы
Характеристики этого типа матрицы:
- Ортогональная матрица никогда не может быть сингулярной матрицей , поскольку ее всегда можно инвертировать. В этом смысле инверсия ортогональной матрицы — это другая ортогональная матрица.
- Любую ортогональную матрицу можно диагонализовать. Тогда мы говорим, что ортогональные матрицы ортогонально диагонализуемы.
- Все собственные значения или собственные значения ортогональной матрицы имеют модуль, равный 1.
- Любая ортогональная матрица, состоящая только из действительных чисел, также является нормальной матрицей.
- Аналогом ортогональной матрицы в среде с комплексными числами является унитарная матрица.
- Очевидно, что единичная матрица является ортогональной матрицей.
- Набор ортогональных матриц размерности n × n, а также операция матричного произведения образуют группу, называемую ортогональной группой. То есть произведение двух ортогональных матриц равно другой ортогональной матрице.
- Кроме того, результат умножения ортогональной матрицы на ее транспонирование может быть выражен дельтой Кронекера:
![Rendered by QuickLaTeX.com \displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d0922008f857f33f46de7551a8ff7cc_l3.png)
- Наконец, определитель ортогональной матрицы всегда равен +1 или -1.
![]()
Решенное упражнение с ортогональными матрицами
Затем мы решим упражнение с ортогональными матрицами.
- По следующей квадратной матрице третьего порядка найдите значения

И

чтобы сделать его ортогональным:
![Rendered by QuickLaTeX.com \displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-892ca58ec5cd36060396cb566902d65d_l3.png)
Чтобы ортогональность матрицы была соблюдена, произведение матрицы на ее транспонирование должно быть равно единичной матрице. ТАК:
![]()
![Rendered by QuickLaTeX.com \displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2dc9ef8c514302f183ca66626cabc1b_l3.png)
Перемножаем матрицы:
![Rendered by QuickLaTeX.com \displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a21a22f3cc9747c310d271c3fe4c5c_l3.png)
Теперь мы можем получить уравнение из верхнего левого угла матриц, поскольку элементы в этой позиции должны совпадать. Еще:
![]()
Решаем уравнение и исключаем неизвестное:
![]()
![]()
![]()
![]()
Однако есть уравнения, которые не имеют положительного решения, например уравнение в правом верхнем углу. Поэтому возможно только отрицательное решение .
С другой стороны, чтобы вычислить переменную
![]()
мы можем сопоставить, например, термины, помещенные во вторую строку первого столбца:
![]()
![]()
Заменив значение
![]()
в уравнении:
![]()
![]()
![]()
Короче говоря, единственное возможное решение:
![]()
Итак, ортогональная матрица, соответствующая этим значениям:
![Rendered by QuickLaTeX.com \displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cb7e7a27658da85f7b0d16b17f1f0815_l3.png)
Приложения ортогональных матриц
Хотя это может показаться не так, поскольку обычно они имеют очень простую форму, ортогональные матрицы очень важны в математике, особенно в области линейной алгебры.
В геометрии ортогональные матрицы представляют собой изометрические преобразования (которые не меняют расстояния и углы) в действительных векторных пространствах, поэтому их называют ортогональными преобразованиями. Более того, эти преобразования являются внутренними изоморфизмами рассматриваемого векторного пространства. Этими преобразованиями могут быть вращения , зеркальные отражения или инверсии .
Наконец, этот тип матрицы также используется в физике, поскольку позволяет изучать движение твердых тел. И они даже используются при формулировании некоторых теорий поля.