▷ Производная косинуса (формула и решенные упражнения)

Здесь вы узнаете, как вывести функцию косинуса (формулу). Вы сможете увидеть примеры производных функций косинуса и попрактиковаться с помощью пошаговых упражнений. Кроме того, мы покажем вам доказательство формулы, что такое вторая производная косинуса и даже производная обратного косинуса.

Что является производной косинуса?

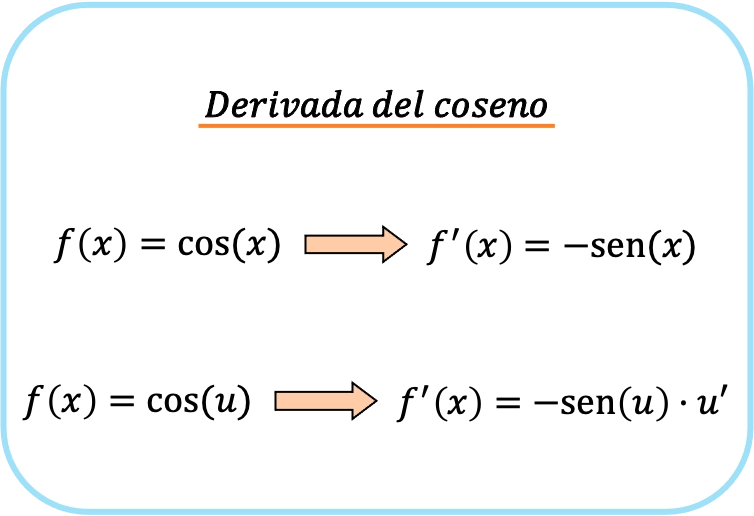
Производная функции косинуса представляет собой синусоидальную функцию с измененным знаком. Другими словами, производная косинуса x равна минус синус x.

$f(x)=\text{cos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x)$

Если в аргументе косинуса присутствует функция, производная косинуса равна произведению минус синуса этой функции на производную функции.

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

Вторая формула эквивалентна первой формуле, но с применением правила цепочки. Итак, вкратце, формула производной косинуса выглядит следующим образом:

Примеры косинусной производной

Теперь, когда мы знаем, что такое формула косинуса, мы объясним несколько примеров такого типа тригонометрических производных, чтобы у вас не осталось сомнений в том, как вывести функцию косинуса.

Пример 1: Производная косинуса 2x

$f(x)=\text{cos}(2x)$

В аргументе косинуса у нас нет одного x, а есть более сложная функция. Поэтому для получения косинуса нам нужно использовать следующую формулу:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

Поскольку производная 2x равна 2, производная косинуса 2x будет минус синус 2x, умноженный на 2.

$f(x)=\text{cos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(2x)\cdot 2=-2\text{sen}(2x)$

Пример 2: Производная косинуса x в квадрате

$f(x)=\text{cos}(x^2)$

Как и в предыдущем примере, в аргументе косинуса у нас есть функция, отличная от функции x, поэтому мы будем использовать цепное правило для получения косинуса:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

Тогда производная x ² равна 2x, следовательно, производная косинуса x, возведенного в степень 2, равна:

$f(x)=\text{cos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(x^2)\cdot 2x$

Пример 3: Производная куба косинуса

$f(x)=\text{cos}^3(2x^6-5x^3)$

Функция косинуса в этом примере состоит из другой функции, поэтому для решения производной нам нужно применить следующую формулу:

$f(x)=\text{cos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sen}(u)\cdot u'$

Таким образом, применив формулу, приходим к производной функции:

$\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}$

➤ Чтобы дифференцировать эту функцию, необходимо также воспользоваться формулой производной потенциальной функции .

Вторая производная косинуса

Далее мы увидим, что вторую производную синуса можно легко вычислить благодаря характеристикам тригонометрических функций.

➤ Примечание. Чтобы понять следующее, вам необходимо знать, что такое производная синуса .

Вторая производная косинуса x равна минус косинусу x. Это может показаться странным, но математически это именно так. Действительно, производная синуса есть косинус и, следовательно, дважды продифференцировав косинус x, снова получим косинус, но с измененным знаком.

$\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}$

Это свойство меняется, если аргумент косинуса не равен x, поскольку в этом случае мы перетаскиваем член правила цепочки:

$\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}$

Производная обратного косинуса

Все тригонометрические функции имеют обратную функцию, поэтому функция косинуса также может быть обратной. Аналогично, обратный косинус дифференцируем.

Производная обратного косинуса функции равна минус производной функции, деленной на квадратный корень из единицы минус квадрат указанной функции.

$f(x)=\text{cos}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Помните, что обратный косинус еще называют арккосинусом.

Например, производная обратного косинуса 3x равна:

$f(x)=\text{cos}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3}{\sqrt{1-(3x)^2}}=-\cfrac{3}{\sqrt{1-9x^2}}$

Решенные упражнения на производную косинуса

Вычислите производную следующих косинус-функций:

$\text{A) } f(x)=\text{cos}(4x)$

$\text{B) } f(x)=\text{cos}(2x^3-5x+1)$

$\text{C) } \displaystyle f(x)=9\text{cos}\left(\frac{x}{3}\right)$

$\text{D) } f(x)=\text{cos}^5(x^2+3x)$

$\text{E) } f(x)=\text{cos}\left(e^{5x}\right)$

$\text{F) } \displaystyle f(x)=9\text{cos}\left(\frac{e^x}{5x}\right)$

Посмотреть решение

$\text{A) } f'(x)=-\text{sen}(4x)\cdot 4 =-4\text{sen}(4x)$

$\text{B) } f'(x)=-\text{sen}(2x^3-5x+1)\cdot (6x^2-5)$

$\text{C) } \displaystyle f'(x)=-9\text{sen}\left(\frac{x}{3}\right)\cdot \frac{1}{3} =-3\text{sen}\left(\frac{x}{3}\right)$

$\text{D) } f'(x)=-5\text{cos}^4(x^2+3x)\cdot \text{sen}(x^2+3x)\cdot (2x+3)$

$\text{E) } f'(x)=-\text{sen}\left(e^{5x}\right)\cdot e^{5x}\cdot 5=-5\text{sen}\left(e^{5x}\right)\cdot e^{5x}$

$\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}$

Доказательство производной косинуса

Наконец, мы математически продемонстрируем формулу производной косинуса x. Для этого воспользуемся определением производной, которое соответствует следующему пределу:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Мы собираемся доказать косинус, поэтому функция равна cos(x):

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\text{cos}(x+h)-\text{cos}(x)}{h}$

Мы не можем разрешить этот предел путем замены, потому что в конечном итоге мы окажемся в неопределенности. Однако мы можем выразить косинус суммы по-другому, применив следующее тригонометрическое тождество:

$\text{cos}(a+b)=\text{cos}(a)\text{cos}(b)-\text{sen}(a)\text{sen}(b)$