На этой странице мы объясним, что такое факторная теорема. Кроме того, мы покажем, для чего используется факторная теорема: делимости многочленов, нахождения корней, факторизации многочленов и т. д. Наконец, вы сможете попрактиковаться, выполняя пошаговые упражнения по факторной теореме.
Что такое факторная теорема?
В математике факторная теорема гласит, что многочлен P(x) делится на другой многочлен формы (xa) тогда и только тогда, когда P(a)=0.
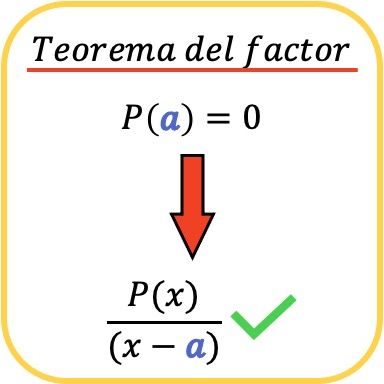
Аналогично, как следствие факторной теоремы, следует, что если многочлен P(x) делится на член (x−a), это означает, что значение a является корнем (или нулем) многочлена P( x ) .
То, что один многочлен делится на другой, означает, что остаток (или остаток) от деления двух многочленов равен нулю. Если вы не совсем помните это понятие, по следующей ссылке вы можете увидеть примеры деления многочленов , там же вы найдете объяснение того, как делить многочлены, и упражнения, решаемые шаг за шагом.
Примеры теорем о факторах
Теперь, когда мы знаем математическое определение факторной теоремы, давайте рассмотрим несколько примеров, чтобы увидеть, как она применяется.
Пример 1
Одним из применений факторной теоремы является выяснение того, делится ли данный многочлен на бином . Давайте посмотрим пример того, как это делается с помощью факторной теоремы:
- Определите, делится ли многочлен P(x) на бином Q(x), оба из которых:
![]()
Во-первых, полином делителя Q(x) является полиномом типа (xa), поэтому мы можем применить факторную теорему для решения проблемы.
Итак, чтобы проверить, можно ли P(x) разделить на Q(x), нам нужно вычислить численное значение многочлена P(x) для x=1, поскольку 1 — это независимый член делящего многочлена с измененным знаком. :
![Rendered by QuickLaTeX.com \begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00216efc4a2e53b0b38de1175e73a5bd_l3.png)
Числовое значение многочлена P(x) при x = 1 дает ноль, поэтому согласно факторной теореме P(x) делится на Q(x), или, другими словами, остаток от деления на оба будет равен нулю.
Мы можем убедиться, что условие делимости выполнено, разделив 2 многочлена по теореме Руффини :
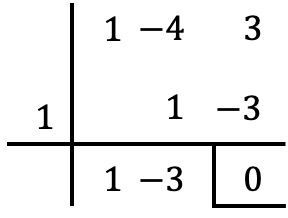
Как вы можете видеть в этом примере, факторная теорема является частным случаем теоремы об остатке (или остатке). Я оставляю вам эту статью, в которой объясняется, что такое теорема об остатках , вы также найдете примеры и упражнения, решенные с ее помощью. И более того, вы сможете увидеть, в чем разница между теоремой об остатках и теоремой о факторах.
Пример 2
Факторную теорему также можно использовать для нахождения корней (или нулей) многочлена. Но, очевидно, чтобы понять задачу такого типа, вам нужно знать , каковы корни многочлена . Если вы все еще не понимаете эту концепцию, вы можете взглянуть на связанную страницу, которая подробно объяснена.
Итак, давайте посмотрим на примере, как факторная теорема применяется для нахождения корня многочлена:
- Учитывая многочлен P(x), вычислите, равен ли один из его корней x=2:
![]()
Применяя факторную теорему, член x=2 будет корнем многочлена P(x), только если числовое значение P(x) для x=2 равно нулю. Итак, нам нужно найти это числовое значение:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-82d50f0361613cb6c540051f8da4bc20_l3.png)
Действительно, числовое значение многочлена P(x) обращается в нуль при x=2, поэтому благодаря факторной теореме мы можем утверждать, что x=2 является корнем многочлена P(x).
Факторизация полиномов с использованием факторной теоремы
Другое применение факторной теоремы — факторизация многочленов . Если вы не знаете, что это такое, факторизация многочлена означает преобразование выражения многочлена в произведение множителей, то есть факторизация многочлена упрощает его алгебраическое выражение.
Таким образом, факториальная теорема устанавливает, что если многочлен P(x) удовлетворяет условию P(a)=0 для данного значения a, то выражение этого многочлена можно разложить на множители в произведение P(x)=(xa) · Q( x), где Q(x) — многочлен, полученный в результате деления многочлена P(x) на (xa).
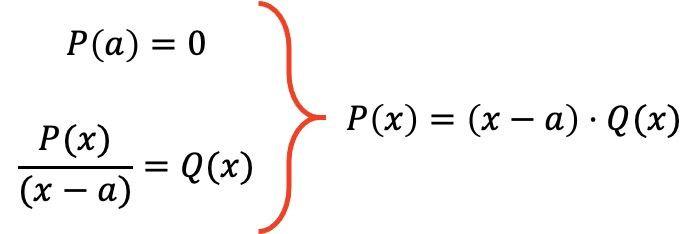
В качестве примера мы факторизуем следующий многочлен, используя теорему о факториале:
![]()
Из предыдущего многочлена мы можем знать, что x=-2 является одним из его корней, поскольку числовое значение многочлена для x=-2 равно нулю:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d94a4657a385e672badeabd7458b376_l3.png)
Поэтому мы делим по правилу Руффини полином P(x) между биномом, образованным x, и этим корнем с измененным знаком, то есть множителем (x + 2):
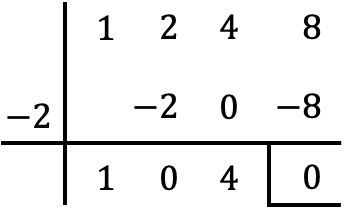
Таким образом, частное деления многочлена равно:
![]()
И, наконец, из факторной теоремы мы можем выразить многочлен P(x) в виде умножения множителя (x+2) на частное, полученное при предыдущем делении:
![]()
Таким образом, мы факторизовали многочлен P(x), но лишь частично. Чтобы полностью факторизовать полином, необходимо применить более длительную процедуру. Мы составили руководство, в котором шаг за шагом учим факторизовать полиномы Руффини . Кроме того, в этой статье мы объяснили все типы факторизации, и вы сможете попрактиковаться с решенными упражнениями. Итак, нажмите на ссылку, чтобы узнать, как факторизовать многочлен из набора.
Решенные задачи по теореме о факторах
Затем мы подготовили несколько упражнений, решаемых шаг за шагом по факторной теореме, чтобы вы могли попрактиковаться и таким образом проверить, поняли ли вы эту теорему. Мы рекомендуем вам попробовать выполнить их самостоятельно, а затем посмотреть, правильно ли вы поняли решение. Также не забывайте, что вы можете оставлять нам свои вопросы ниже в комментариях! ❓❓💬💬
Упражнение 1
Используйте теорему о факториале, чтобы определить, делится ли многочлен P(x) на бином Q(x), и если да, то найдите корень многочлена и факторизуйте его.
![]()
В этом случае полиномиальный делитель Q(x) представляет собой бином, состоящий только из x и независимого члена. Итак, чтобы показать, что многочлен P (x) можно разделить на другой многочлен Q (x) с помощью факториальной теоремы, мы должны оценить числовое значение многочлена P (x) в независимом члене полинома делителя с измененным знаком: то есть при x=3:
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e8ac752f8e16fae1d66386e9d2a02a0_l3.png)
Числовое значение многочлена P(x) при x=3 эквивалентно 14, то есть отлично от нуля. Итак, согласно факторной теореме, P(x) НЕ делится на Q(x), поскольку остаток от деления не равен нулю.
Упражнение 2
С помощью факториальной теоремы выяснить, делится ли многочлен P(x) на бином Q(x), и если да, то найти корень многочлена P(x) и факторизовать его.
![]()
В этом случае полиномиальный делитель Q(x) представляет собой бином, состоящий только из x и независимого члена, поэтому мы можем применить теорему о факториале.
А чтобы проверить, можно ли разделить многочлен P(x) на многочлен Q(x), необходимо найти числовое значение многочлена P(x) для независимого члена многочлена Q(x), изменившего знак, это т. е. при x=-1:
![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34b63772a1b44bee2c746d94b6ca4785_l3.png)
В этой задаче числовое значение многочлена при x=-1 равно нулю, поэтому P(x) делится на Q(x).
Затем мы можем вывести с помощью факториальной теоремы, что x=-1 является корнем многочлена P(x), поскольку числовое значение P(x) при x=-1 обращается в нуль.
Таким образом, поскольку x=-1 является корнем многочлена P(x), чтобы факторизовать его, просто разделите его на x+1. И для этого мы собираемся использовать метод Руффини:
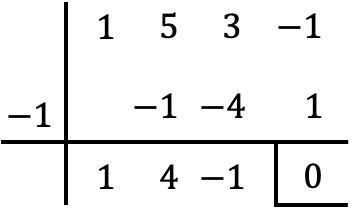
Итак, результат операции:
![]()
Поэтому мы можем факторизовать полином P(x) следующим образом:
![]()
Упражнение 3
С помощью факториальной теоремы найдите, делится ли многочлен P(x) на бином Q(x), и если да, то также найдите корень многочлена P(x) и факторизуйте его.
![]()
В этом случае многочлен, делящий Q(x), представляет собой бином, образованный только x и независимым членом, поэтому мы можем использовать факторную теорему.
А чтобы проверить, делится ли многочлен P(x) на многочлен Q(x), мы должны определить числовое значение многочлена P(x) для независимого члена многочлена Q(x), изменившего знак, то есть- то есть при x =-3:
![Rendered by QuickLaTeX.com \begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef8bb895fe041193d71351ffadb94f2f_l3.png)
В этом случае числовое значение многочлена при x=-3 равно нулю, поэтому действительно P(x) делится на Q(x).
По этой причине из факториальной теоремы мы выводим, что x=-3 является корнем многочлена P(x), поскольку P(-3) равно нулю.
Итак, поскольку x=-3 является корнем многочлена P(x), чтобы факторизовать его, мы должны разделить его на x+3. И для этого воспользуемся правилом Руффини:
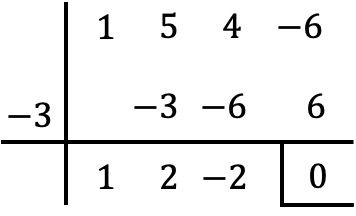
Итак, результат деления:
![]()
И, следовательно, мы можем факторизовать полином P(x) следующим образом:
![]()
Что вы думаете о факторной теореме? Как вы думаете, это полезно в алгебре? Читаем вас в комментариях!
👀⬇⬇⬇👀