Эта страница, безусловно, является наиболее полным объяснением существующей матрицы Гессе. Здесь объясняется понятие матрицы Гессе, способы ее расчета с примерами и даже есть несколько решенных упражнений для практики. Дополнительно вы сможете узнать, как рассчитываются максимальное и минимальное значения функции многих переменных, а также является ли она вогнутой или выпуклой функцией. И, наконец, вы также найдете утилиты и приложения для матрицы Гессе.
Что такое матрица Гессе?
Определение матрицы Гессе (или гессиана) следующее:
Матрица Гессе — это квадратная матрица размерности n × n, составленная из частных вторых производных функции n переменных.
Эта матрица также известна как гессиан или даже в некоторых учебниках по математике ее называют дискриминантной. Но наиболее распространенный способ ее называть — матрица Гессе.
Таким образом, формула матрицы Гессе выглядит следующим образом:

Следовательно, матрица Гессе всегда будет квадратной матрицей, размерность которой будет равна количеству переменных в функции. Например, если функция имеет 3 переменные, матрица Гессе будет иметь размерность 3×3.
Кроме того, теорема Шварца (или теорема Клеро) говорит, что порядок дифференцирования не имеет значения, т.е. частично выводится сначала по переменной
![]()
тогда по переменной
![]()
сводится к частичному дифференцированию по
![]()
тогда уважение
![]()
.
![]()
Следовательно, матрица Гессе является симметричной матрицей, или, другими словами, она обладает симметрией, осью которой является ее главная диагональ.
Любопытно, что матрица Гессе названа в честь Людвига Отто Гессе, немецкого математика XIX века, внесшего очень важный вклад в область линейной алгебры.
Пример расчета матрицы Гессе
Давайте посмотрим пример того, как найти матрицу Гессе размерности 2 × 2:
- Вычислите матрицу Гессе в точке (1,0) следующей функции:
![]()
Сначала нам нужно вычислить частные производные первого порядка:
![]()
![]()
Как только мы уже знаем первые производные, мы вычисляем все частные производные второго порядка:
![]()
![]()
![]()
Следовательно, теперь мы можем найти матрицу Гессе по формуле для матриц 2×2:
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-926f350fe0ac3184ec0b563b57fd6041_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b7f3d45918645a5b6019896ed45eda75_l3.png)
Таким образом, матрица Гессе, оцененная в точке (1,0), будет:
![Rendered by QuickLaTeX.com \displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bdccfc61f7befe6c75f66c8a4658f3e6_l3.png)
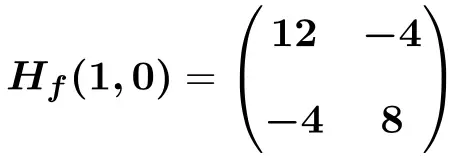
Решенные проблемы матриц Гессе
Упражнение 1
Вычислите матрицу Гессе следующей функции с двумя переменными в точке (1,1):
![]()
Сначала нам нужно найти частные производные первого порядка функции:
![]()
![]()
После того, как мы уже вычислили первые производные, приступаем к решению всех частных производных второго порядка:
![]()
![]()
![]()
Таким образом, матрица Гессе определяется следующим образом:
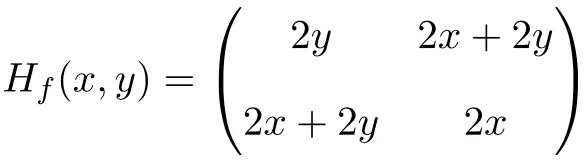
Наконец, остается только вычислить матрицу Гессе в точке (1,1):
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5353c0229942269e07455047284f92b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf00fccdb37a19388e76b5a84a408d02_l3.png)
Упражнение 2
Вычислите гессиан в точке (1,1) следующей функции двух переменных:
![]()
Сначала нам нужно вычислить частные производные первого порядка функции:
![]()
![]()
Получив первые производные, мы вычисляем частные производные второго порядка функции:
![]()
![]()
![]()
Таким образом, матрица Гессе функции представляет собой квадратную матрицу размерности 2×2:
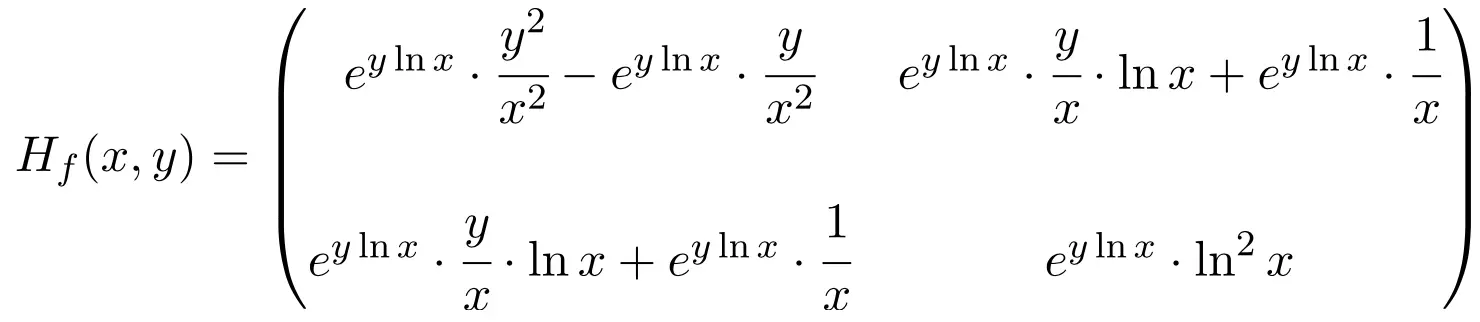
Наконец, остается только вычислить матрицу Гессе в точке (1,1):
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c316cc61e6d007e5d034274e0f494520_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e456b856c722a140d73ade63f13ec9f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-929fbf6e7f0f90110d11d4ccd51fd51a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce780ddb8c09515afccfb2da2d842584_l3.png)
Упражнение 3
Найдите матрицу Гессе в точке
![]()
следующей функции с тремя переменными:
![]()
Сначала вычислим частные производные первого порядка функции:
![]()
![]()
![]()
Получив первые производные, мы вычисляем частные производные второго порядка функции:
![]()
![]()
![]()
![]()
![]()
![]()
Так что матрица Гессе функции представляет собой квадратную матрицу размерности 3×3:
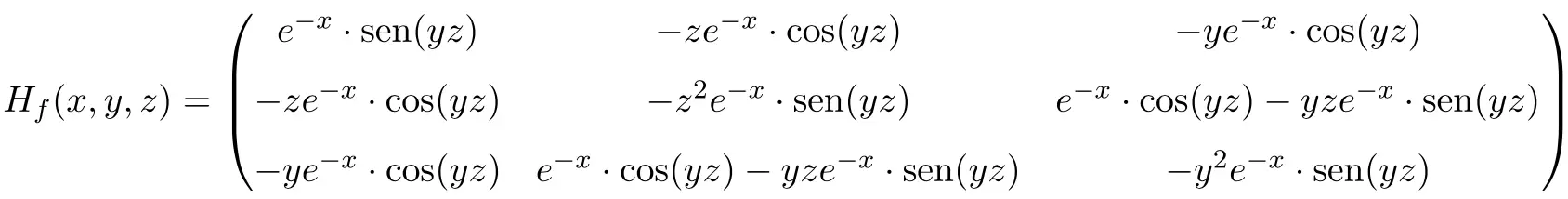
Наконец, мы заменяем переменные соответствующими значениями в точке
![]()
![Rendered by QuickLaTeX.com \displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e198192f67babd81228caa53b66e8a0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ce9c6b4cfcddfb0c2eb51db1189c653_l3.png)
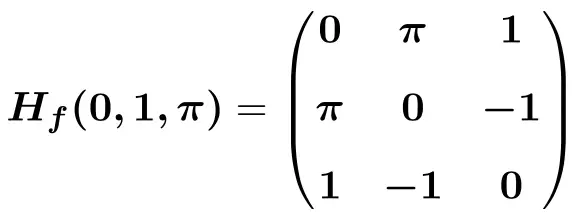
Упражнение 4
Определите матрицу Гессе в точке (2,-1,1,-1) следующей функции с 4 переменными:
![]()
Первым шагом является нахождение частных производных первого порядка функции:
![]()
![]()
![]()
![]()
Теперь решаем частные производные второго порядка функции:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, выражение матрицы Гессе 4 × 4, полученное путем решения всех частных производных, имеет следующий вид:
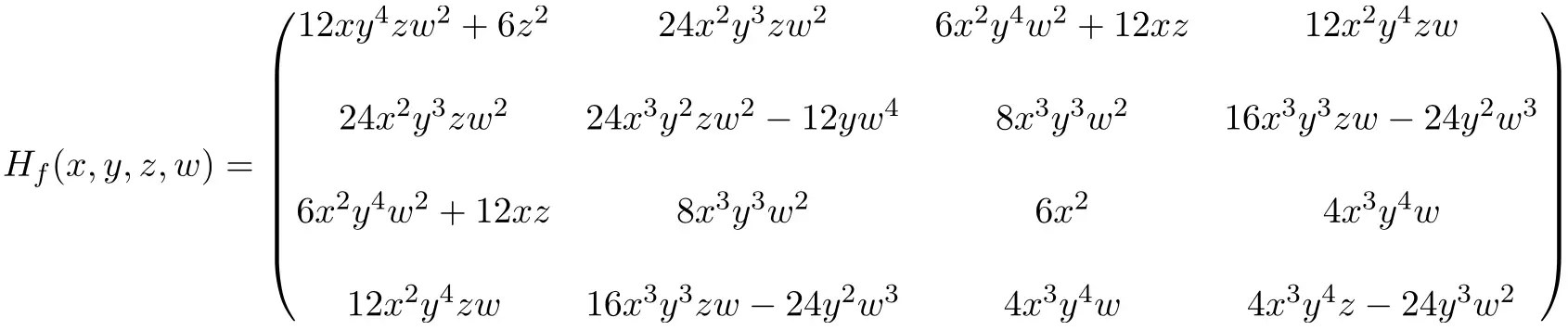
Наконец, мы заменяем неизвестные их соответствующие значения в точках (2,-1,1,-1) и выполняем вычисления:
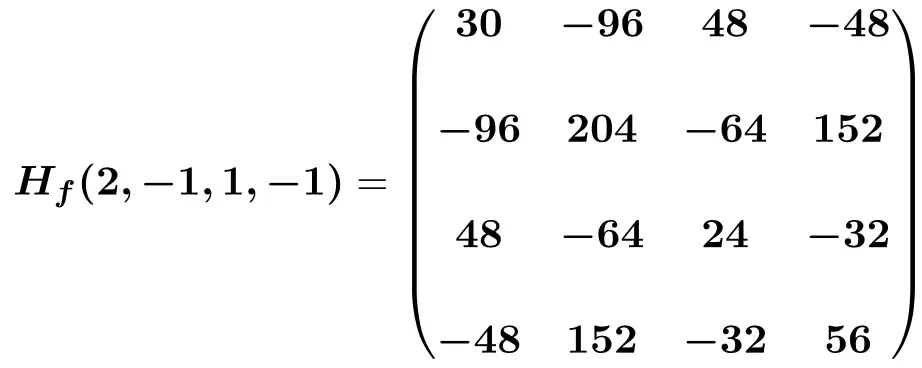
Как узнать, когда матрица Гессе положительна, отрицательна или неопределенна?
Как мы увидим позже, знание того, является ли матрица Гессе положительно-полуопределенной, положительно-определенной, отрицательно-полуопределенной, отрицательно-определенной или неопределенной матрицей, очень полезно. Итак, давайте посмотрим, как мы можем это узнать:
Критерий собственных значений (или собственных значений)
Один из способов узнать, какой это тип матрицы, — просмотреть собственные значения (или собственные значения) матрицы Гессе:
- Матрица Гессе является положительно-полуопределенной, если она имеет собственные значения (или собственные значения), равные и большие нуля. То есть у него есть положительные собственные значения и хотя бы одно, равное 0:
![]()
- Матрица Гессе является положительно определенной , если все ее собственные значения (или собственные значения) исключительно больше 0 (положительные):
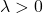 отрицательной полуопределенной, если она имеет собственные значения (или собственные значения), равные нулю и меньшие него. То есть он имеет отрицательные собственные значения и хотя бы одно, равное 0:
отрицательной полуопределенной, если она имеет собственные значения (или собственные значения), равные нулю и меньшие него. То есть он имеет отрицательные собственные значения и хотя бы одно, равное 0:
![]()
- Матрица Гессе является отрицательно определенной , если все ее собственные значения (или собственные значения) меньше 0 (отрицательны):
![]()
- Матрица Гессе не определена , когда она имеет положительные и отрицательные собственные значения (или собственные значения):
![]()
критерий Сильвестра
Другой способ узнать, к какому типу относится матрица Гессе, — использовать критерий Сильвестра, хотя эта теорема позволяет нам узнать только, является ли она положительно определенной, отрицательно определенной или неопределенной. Но иногда его можно использовать намного быстрее, поскольку вычисления, как правило, проще.
Таким образом, критерий Сильвестра выглядит следующим образом:
- Если все главные миноры матрицы Гессе больше 0, это положительно определенная матрица.
- Если главные миноры матрицы Гессе с четным индексом больше 0, а миноры с нечетным индексом меньше 0, это отрицательно определенная матрица.
- Если все главные миноры матрицы Гессе не равны 0 и ни одно из двух предыдущих условий не выполнено, это неопределенная матрица.
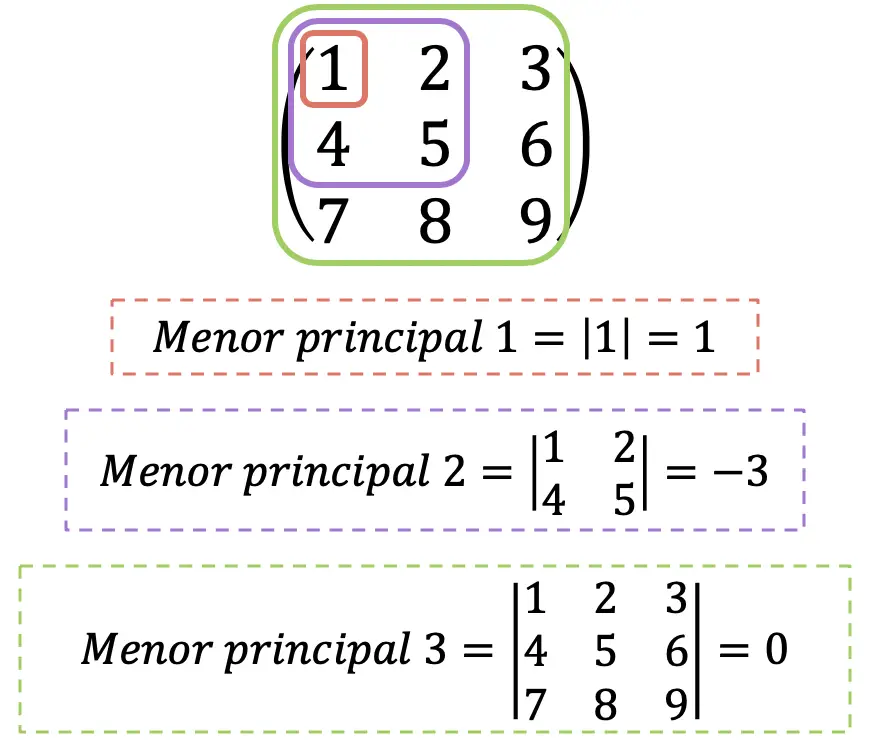
Очевидно, что максимальный главный минор матрицы Гессе всегда будет совпадать с ее определителем. Исключительно в информационных целях определитель матрицы Гессе также называют «гессианом», хотя мы не будем здесь этого делать во избежание путаницы.
Как вычислить максимум или минимум функции с помощью матрицы Гессе
Узнав, как рассчитать матрицу Гессе, вы, вероятно, задаетесь вопросом: а для чего используется эта матрица?
Ну, одно из применений матрицы Гессе — найти максимум или минимум функции с более чем одной переменной. Вот пошаговое объяснение того, как рассчитать максимумы и минимумы:
- Сначала вычисляются критические точки функции многих переменных. Для этого вычисляем градиент или матрицу Якоби функции, приравниваем ее к 0 и решаем уравнения.
- Рассчитывается матрица Гессе.
- Критические точки, найденные на шаге 1, подставляются в матрицу Гессе. Таким образом, мы получим столько матриц Гессе, сколько критические точки имеют функцию.
- Мы посмотрим, к какому типу относится каждая матрица Гессе. То есть мы смотрим, является ли оно положительно определенным, отрицательно определенным, неопределенным и т. д.
- Если матрица Гессе положительно определена, критическая точка представляет собой относительный минимум функции.
- Если матрица Гессе отрицательно определена, критическая точка представляет собой относительный максимум функции.
- Если матрица Гессе не определена, критическая точка является седловой точкой .
Пример вычисления максимумов и минимумов функции многих переменных
Чтобы увидеть, как это делается, вот пример вычисления и классификации относительных экстремумов функции с использованием матрицы Гессе:
- Найдите все относительные экстремумы следующей функции многих переменных:
![]()
Первое, что нам нужно сделать, это вычислить матрицу Якобиана функции, которая в данном случае будет совпадать с градиентом, поскольку является скалярной функцией:
![]()
Теперь нам необходимо определить критические точки, для этого приравниваем полученные уравнения к 0 и решаем систему уравнений:
![]()
![Rendered by QuickLaTeX.com \displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d851eb626a9bd385aec8f68c9df71a39_l3.png)
Итак, критическая точка, которую мы нашли, — это (0,-2).
Как только критическая точка функции найдена, мы должны вычислить матрицу Гессе:
![Rendered by QuickLaTeX.com \displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-702fa5f5c3e3d872e1ec0dad0e3216c7_l3.png)
И, очевидно, матрица Гессе, вычисленная в критической точке, та же самая:
![Rendered by QuickLaTeX.com \displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b56ffff28d1a9b98c9848891ae924eb_l3.png)
Чтобы увидеть, что это за матрица, воспользуемся критерием Сильвестра. Поэтому мы решаем основные миноры матрицы:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8](https://mathority.org/wp-content/ql-cache/quicklatex.com-d66efe9fca481475009bb1703939e4f6_l3.png)
Главный минор 1 (нечетный) положителен, а главный минор 2 (четный) отрицательен, поэтому по критерию Сильвестра это неопределенная матрица. И, следовательно, критическая точка (0,-2) является седловой.
Определение вогнутости или выпуклости функции с помощью матрицы Гессе
Другое использование матрицы Гессе — узнать, является ли функция вогнутой или выпуклой. А это можно определить по следующей теореме:
Быть
![]()
открытый набор и
![]()
функция, вторые производные которой непрерывны, ее вогнутость и выпуклость определяются матрицей Гессе:
- Функция

является выпуклым во всем

тогда и только тогда, когда его матрица Гессе положительно полуопределена в каждой точке множества.
- Функция

строго выпукла во всем

тогда и только тогда, когда его матрица Гессе положительно определена в каждой точке множества.
✓ Поэтому, если
![]()
является выпуклой функцией в точке, где матрица Якоби также обращается в нуль, эта точка является локальным минимумом .
- Функция

в целом вогнутый

тогда и только тогда, когда его матрица Гессе отрицательно полуопределена в каждой точке множества.
- Функция

в целом строго вогнутый

тогда и только тогда, когда его матрица Гессе отрицательно определена в каждой точке множества.
✓ Поэтому, если
![]()
— функция, вогнутая в точке, где матрица Якоби также обращается в нуль, эта точка является локальным максимумом .
Ниже у вас есть пример выпуклой функции и еще один пример вогнутой функции, представленной в трехмерном пространстве:
выпуклая функция
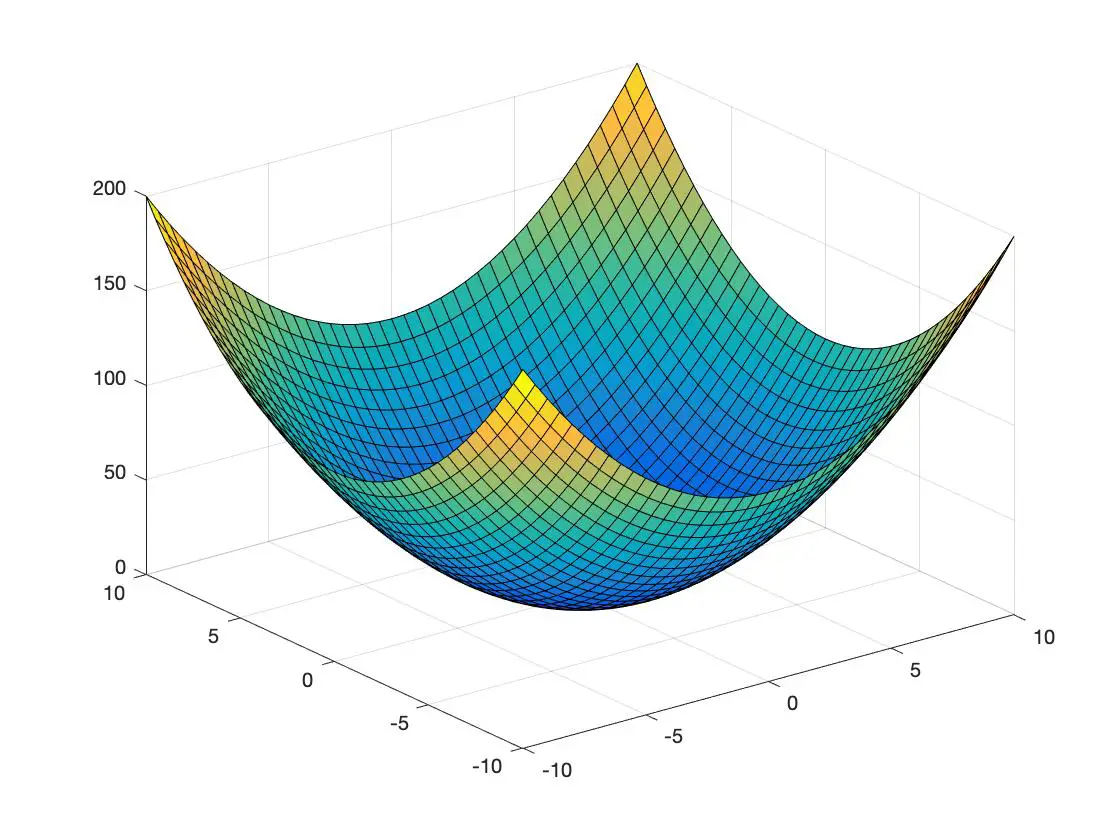
вогнутая функция
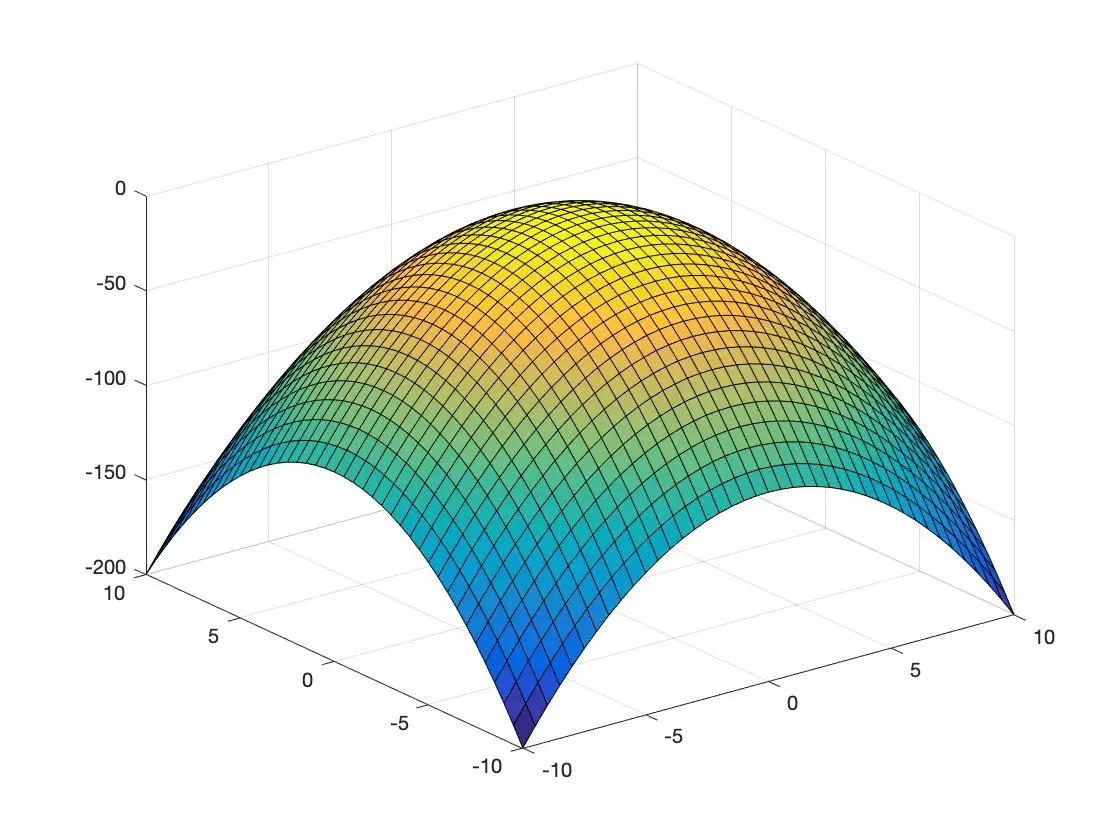
Дополнительные применения матрицы Гессе
Основные способы применения матрицы Гессе мы уже видели, однако у нее есть и другие применения. Мы объясним их ниже для самых любопытных.
Полином Тейлора
Разложение полинома Тейлора для функций двух и более переменных в точке
![]()
начинается так:
![]()
Как видите, члены второго порядка разложения Тейлора задаются матрицей Гессе, вычисляемой в точке разложения многочлена.
Матрица из мешковины с окантовкой
Другое применение матрицы Гессе — вычисление минимумов и максимумов многомерной функции.
![]()
ограничен другой ролью
![]()
. Для решения этой задачи используется ограниченная матрица Гессе и выполняется следующая процедура:
Шаг 1: Рассчитывается функция Лагранжа, которая определяется следующим выражением:
![]()
Шаг 2: Находятся критические точки функции Лагранжа. Для этого вычисляем градиент функции Лагранжа, приравниваем уравнения к 0 и решаем уравнения.
![]()
![]()
Шаг 3: Для каждой найденной точки мы вычисляем ограниченный гессиан, который определяется следующей матрицей:
![Rendered by QuickLaTeX.com \displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3d1b2b04de9559a521e6704151c27bc4_l3.png)
Шаг 4: Определяем для каждой критической точки, является ли она максимумом или минимумом:
- Это будет локальный максимум функции

при функциональных ограничениях
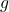
если последние nm (где n — количество переменных, а m — количество ограничений) главные миноры граничной матрицы Гессе, оцененной в критической точке, имеют чередующиеся знаки, начиная с отрицательного.
- Это будет локальный минимум функции

при функциональных ограничениях
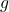
если последние nm (где n — количество переменных, а m — количество ограничений) главные миноры точной матрицы Гессе, оцененной в критической точке, все имеют отрицательные знаки.
Следует иметь в виду, что относительные минимумы или максимумы одной ограниченной функции по отношению к другой не обязательно должны быть таковыми для неограниченной функции. Таким образом, матрица Гессе с границами полезна только для задач такого типа.
Связь с другими операциями
Наконец, матрица Гессиана также связана с другими важными операциями или матрицами, в основном с матрицей Якобиана и оператором Лапласа.
Связь с матрицей Якобиана
Матрица Гессе функции
![]()
– матрица Якоби градиента той же функции:
![]()
Оператор Лапласа
След матрицы Гессе эквивалентен оператору Лапласа :
![]()
Это равенство легко доказать, поскольку определением оператора Лапласа является дивергенция градиента функции:
![]()
Следовательно, его выражение таково:
![]()
И эта сумма является лишь следом матрицы Гессе, поэтому эквивалентность доказана.