Треугольник Тартальи (или Паскаля)

На этой странице мы объясним, что такое треугольник Тартальи, также называемый треугольником Паскаля. Узнаем, как математически построить треугольник Тартальи (или Паскаля), а также для чего он используется и каковы все его свойства. Наконец, мы покажем, как и когда возник этот очень важный треугольник.

Что такое треугольник Тартальи (или Паскаля)?

Треугольник Тартальи , также называемый треугольником Паскаля , представляет собой математическое представление упорядоченных целых чисел в форме треугольника. Треугольник Тартальи (или Паскаля) используется для математических расчетов.

Это определение треугольника Тартальи или Паскаля, но вы наверняка лучше поймете эту концепцию с изображением треугольника:

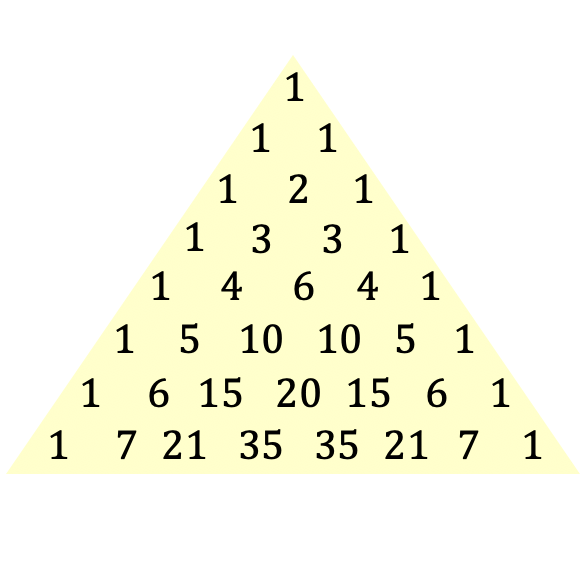
Треугольник Тартальи еще называют треугольником Паскаля в честь французского философа и математика Блеза Паскаля, который ввел это треугольное выражение в 1654 году, хотя этот треугольник известен уже с древних времен. Ниже мы углубимся в историю этого конкретного треугольника.

Как устроен треугольник Тартальи или Паскаля?

Как вы видели в треугольнике Паскаля (или Тартальи), чисел очень много, но это не значит, что мы должны знать их наизусть (слава богу). Существует формула, позволяющая легко найти все числа в треугольнике Паскаля или Тартальи, достаточно решить простые суммы.

Чтобы построить треугольник Тартальи или Паскаля, вы начинаете с вершины треугольника, которая всегда равна 1, а затем вычисляются линии ниже. Каждое число в следующих строках представляет собой сумму двух чисел непосредственно над ним, за исключением концов строк, которые всегда равны 1.

Поэтому вы можете вычислить столько линий треугольника Тартальи, сколько захотите, ведь вы можете последовательно добавлять линии, складывая числа.

Для чего нужен треугольник Тартальи или Треугольник Паскаля?

Уметь строить треугольник Тартальи — это очень хорошо, но… для чего нужен этот арифметический треугольник? Что ж, треугольник Тартальи (или Паскаля) имеет множество приложений в математике, особенно в области алгебры.

комбинаторные числа

Прежде всего, треугольник Тартальи используется для непосредственного вычисления комбинаторных чисел , также называемых биномиальными коэффициентами. Если вы не знаете, что это за типы операций, вы можете поискать их на нашем сайте (у нас есть поисковая система справа вверху), потому что мы написали подробную статью, в которой объясняем, как они решаются, и вы там. также найдете примеры и упражнения, решаемые шаг за шагом. Вкратце, алгебраическое выражение комбинаторного числа выглядит следующим образом:

$\displaystyle \begin{pmatrix} n \\ k \end{pmatrix}$

Что ж, все комбинаторные числа можно легко определить с помощью треугольника Тартальи, поскольку решение каждого биномиального коэффициента эквивалентно числу этого треугольного выражения, как показано на следующем рисунке:

комбинаторные числа треугольника Тартальи или Паскаля

Например, комбинаторное число

$\displaystyle \begin{pmatrix} 4 \\ 2 \end{pmatrix}$

возвращает 6, потому что в треугольнике Тартальи вместо него стоит 6.

Итак, если вы знаете, как построить треугольник Тартальи или Паскаля, вы сможете быстро и без использования их формулы вычислить любое комбинаторное число.

Бином Ньютона

Другое использование треугольника Тартальи (или Паскаля) — вычисление степеней биномов (нажмите на эту ссылку, чтобы узнать, что такое бином).

Примером потенциирования бинома являются известные тождества, такие как:

$(a+b)^2$

Замечательные тождества очень важны для математики, поскольку позволяют нам экономить множество вычислений и решать сложные операции напрямую и быстро. Вот почему мы рекомендуем перейти по следующей ссылке, если вы все еще не знаете , что такое известные личности .

Как вы видели по предыдущей ссылке, известные продукты можно решить непосредственно с помощью их формул. Но… что произойдет, если пару возвести в куб или в более высокую степень?

$\begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}$

Что ж, эти биномы можно очень просто вычислить с помощью треугольника Тартальи благодаря биномиальной теореме (или биному Ньютона). Несмотря на то, что этот метод освоен, его можно быстро применить, но чтобы его хорошо объяснить, вам понадобится целая страница. Поэтому, если вас больше интересует, как решать биномы этого типа, нажмите на связанную страницу, и вы увидите, как это делается.

Комбинаторика

Треугольник Тартальи или треугольник Паскаля также можно использовать для определения комбинаций и вероятностей.

Если мы когда-нибудь столкнемся с проблемой, когда нам нужно будет определить, сколько различных групп можно составить из группы независимо от порядка, мы можем использовать треугольник Тартальи.

Например, если у нас есть 5 карт, чтобы узнать, сколькими способами мы можем выбрать 3, достаточно перейти к третьему столбцу (первый столбец — ноль) пятой строки (первая строка — тоже строка 0) треугольника Тартальи. Число в этой позиции (10) соответствует количеству возможностей выбрать 3 карты.

$1 \quad 5 \quad 10 \quad \color{blue}\boxed{ \color{black}10} \color{black} \quad 5 \quad 1$

Итак, из 5 карт можно сформировать 10 различных групп по три карты.

Свойства треугольника Тартальи или треугольника Паскаля

Треугольник Тартальи, также называемый треугольником Паскаля, имеет следующие характеристики:

Треугольник Тартальи (или Паскаля) симметричен, то есть вертикальная линия, разделяющая весь треугольник на два равных равносторонних треугольника, является осью симметрии.

Горизонтальная сумма всех чисел в любой строке треугольника Паскаля равна степени 2.

свойства треугольника Тартальи или треугольника Паскаля

Важны также диагонали треугольника Тартальи: числа на первой диагонали (внешней диагонали) равны единицам, вторая диагональ образована последовательностью всех натуральных чисел, третья диагональ соответствует треугольным числам, а четвертая диагональ составлена тетрагональных (или тетраэдрических) чисел.

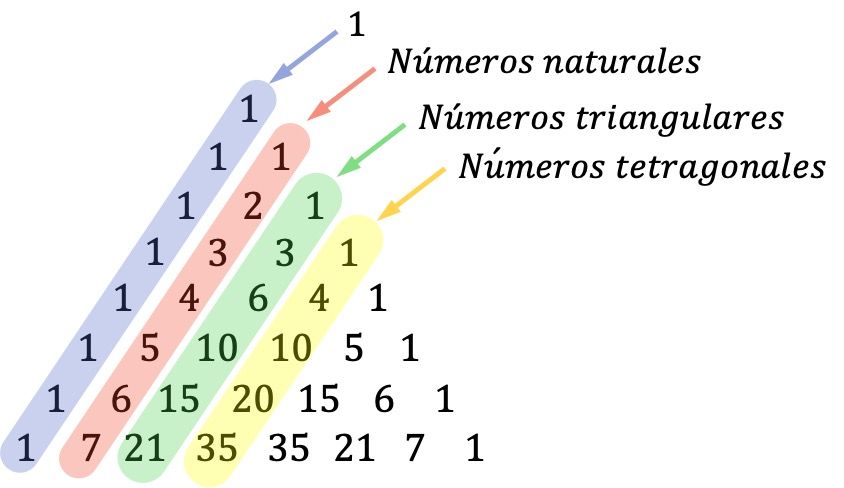
Треугольник Тартальи или треугольные и тетрагональные числа Паскаля

Треугольные числа – это числа, которые можно представить в виде треугольника. А тетрагональные числа – это те, которые образуют треугольные пирамиды.

Если вы не знаете, что такое треугольные или тетрагональные числа, ничего не получится, это просто курьез по поводу треугольника Тартальи. Однако вам необходимо знать значение натуральных чисел (числ, используемых для подсчета элементов).

За исключением числа 1, если первое число в строке является простым числом, все числа в этой строке делятся на это число. Например, в восьмом ряду (1-7-21-35-35-21-7-1) числа 7, 21 и 35 можно разделить на 7 (семь – простое число).

Еще одна особенность треугольника Тартальи в том, что ряд Фибоначчи можно найти, сложив диагонали определенным образом:

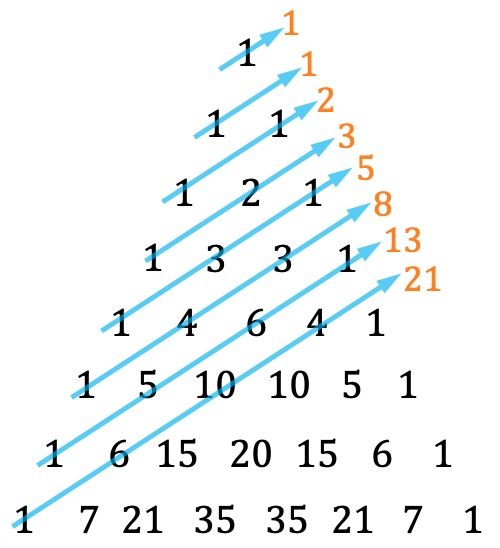
тарталья или треугольник Паскаля ряд Фибоначчи

Помните, что каждый член последовательности Фибоначчи равен сумме двух предыдущих, причем первые два члена равны 1 и 1. Таким образом, числа, принадлежащие последовательности Фибоначчи, равны: 1, 1, 2, 3, 5, 8. , 13, 21, 34, 55, 89, 144, 233,…

Если сложить два последовательных числа из третьей диагонали треугольника Паскаля (1-3-6-10-15-…), то получится полный квадрат (1, 4, 9, 16, 25,…).

Если мы раскрасим четные числа треугольника Паскаля в один цвет, а нечетные числа в другой цвет, мы получим фигуру треугольника Серпинского — знаменитого геометрического набора. Ниже вы можете увидеть треугольник Паскаля высотой 512, представленный нечетными числами черного цвета и четными числами белого цвета:

Треугольник Серпинского Татальи или треугольник Паскаля

Гипотеза Сингмастера гласит, что количество раз, когда встречается каждое число больше 1, конечно. Другими словами, хотя количество строк в треугольнике Тартальи бесконечно, количество раз, когда появляется каждое число, кроме 1, конечно. Любопытно, что число 3003 — единственное известное на сегодняшний день число, которое встречается в треугольнике до восьми раз.

История треугольника Тарталья или Паскаля

Теперь, когда мы знаем, как выглядит треугольник Тартальи, давайте посмотрим, когда был изобретен этот особенный математический треугольник.

Хотя название арифметического треугольника в основном приписывают известным учёным Тарталье и Паскалю, этот алгебраический треугольник уже использовался и раньше.

Первая запись о треугольнике, образованном биномиальными коэффициентами, датируется X веком в Индии. Однако его свойства начали изучать персы, в частности математики Аль-Караджи (953–1029) и Омар Хайям (1048–1131). Именно поэтому в Иране он был популяризирован как треугольник Хайяма-Паскаля или даже просто треугольник Хайяма .

Этот треугольник начал привозиться в Китай в 11 веке математиком Цзя Сянем, но позднее, в 13 веке, Ян Хуэй представил его как арифметический треугольник . И по этой причине в азиатской стране его называют треугольником Ян Хуэй .

Математический треугольник достиг европейского континента позже через немца Петра Апиана, специально опубликованного в 1527 году в его книге Rechnung . Отсюда знаменитый итальянский алгебраист Никколо Фонтана Тарталья углубленно изучал треугольник в первой половине 16 века, и в его честь в таких странах, как Италия, он известен как треугольник Тартальи.

Наконец, француз Блез Паскаль продемонстрировал многие свойства треугольника, изученные в его публикации «Трактата об арифметическом треугольнике» в 1654 году, отсюда и название «треугольник Паскаля». Следует отметить, что некоторые из этих свойств уже были известны, но именно Паскаль провел их демонстрацию методом математической индукции.

Треугольник тартальи (или паскаля)