На этой странице мы объясняем, что такое независимый член многочлена и как он рассчитывается. Кроме того, вы сможете увидеть несколько примеров того, как определить независимый член разных многочленов, и даже попрактиковаться на решенных упражнениях.
Что такое независимый член многочлена?
Определение независимого члена многочлена следующее:
В математике независимым членом многочлена является член, не имеющий переменной. Следовательно, независимый член многочлена соответствует моному нулевой степени многочлена.
Например, независимый член следующего многочлена равен 7:
![]()
В многочлене из предыдущего примера член, который не имеет буквальной части, то есть не имеет буквы x, равен числу 7. По этой причине независимым членом указанного многочлена является 7.
Хотя независимый член многочлена кажется очень простой концепцией, знайте, что он очень полезен для некоторых полиномиальных вычислений. Например, процедура нахождения корней многочлена начинается с его независимого члена. Если вы хотите узнать больше о том, как найти корни (или нули) многочлена, вы можете перейти по этой ссылке, где вы также можете увидеть примеры и попрактиковаться в упражнениях, решаемых шаг за шагом.
Примеры независимых членов многочленов
Как только мы узнаем значение независимого члена многочлена, мы увидим несколько примеров того, как найти независимый член многочлена:
- Пример независимого члена многочлена 4-й степени:
![]()
Полином в этом примере является моническим многочленом, а член, не имеющий переменной, равен 5, поэтому значение независимого члена многочлена равно 5.
- Пример независимого члена полинома 5-й степени:
![]()
Элемент этого многочлена, который не сопровождается переменной x, равен -2, поэтому он является независимым членом многочлена. Обратите внимание, что отрицательный знак числа также входит в независимый член.
- Пример независимого члена полинома 8-й степени:
![]()
Все мономы в этом многочлене имеют переменную, кроме +1, поэтому независимый член многочлена равен +1.
Наконец, одним из свойств независимого члена является то, что числовое значение многочлена при x=0 всегда равно его независимому члену. Если вас больше интересует эта любопытная вещь, вы можете проконсультироваться на связанной странице, как рассчитывается числовое значение многочлена, кроме того, вы также найдете несколько примеров того, как это делается, и сможете попрактиковаться с решенными упражнениями. шаг за шагом.
Решение упражнения на независимый член многочлена
Чтобы закончить усвоение того, что такое независимый член многочлена, мы предлагаем вам выполнить упражнение, которое мы решаем ниже:
- Учитывая полином
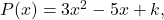
вычисляет значение независимого члена

чтобы оно было заполнено
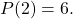
Первое, что нужно сделать для решения этой проблемы, — это попытаться определить
![]()
Еще:
![]()
Рассчитаем мощность:
![]()
Делаем умножения:
![]()
И вычитаем как слагаемые:
![]()
Таким образом, чтобы условие утверждения было выполнено, необходимо полученное алгебраическое выражение приравнять к 6:
![]()
![]()
Поэтому достаточно решить полученное уравнение:
![]()
![]()
В заключение следует отметить, что независимый член многочлена должен быть равен 4.
Наконец, вы должны знать, что независимый член многочлена также важен для правильного применения правила Руффини. Если вы не знаете, что это такое, правило Руффини — это метод, используемый для быстрого деления многочленов. Здесь вы можете увидеть , как применять правило Руффини и как оно связано с независимым членом многочлена.