На этой странице вы увидите, что такое правило Крамера, а также найдете примеры и упражнения с решением систем уравнений по правилу Крамера.
Что такое правило Крамера?
Правило Крамера — это метод решения систем уравнений с помощью определителей. Давайте посмотрим, как он используется:
Рассмотрим систему уравнений:
![Rendered by QuickLaTeX.com \begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e0141f3451719f665ef28e4061489551_l3.png)
Матрица A и расширенная матрица A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d628a13ec7de4b3ba7a301c0a5d8ac6_l3.png)
Правило Крамера гласит, что решением системы уравнений является:
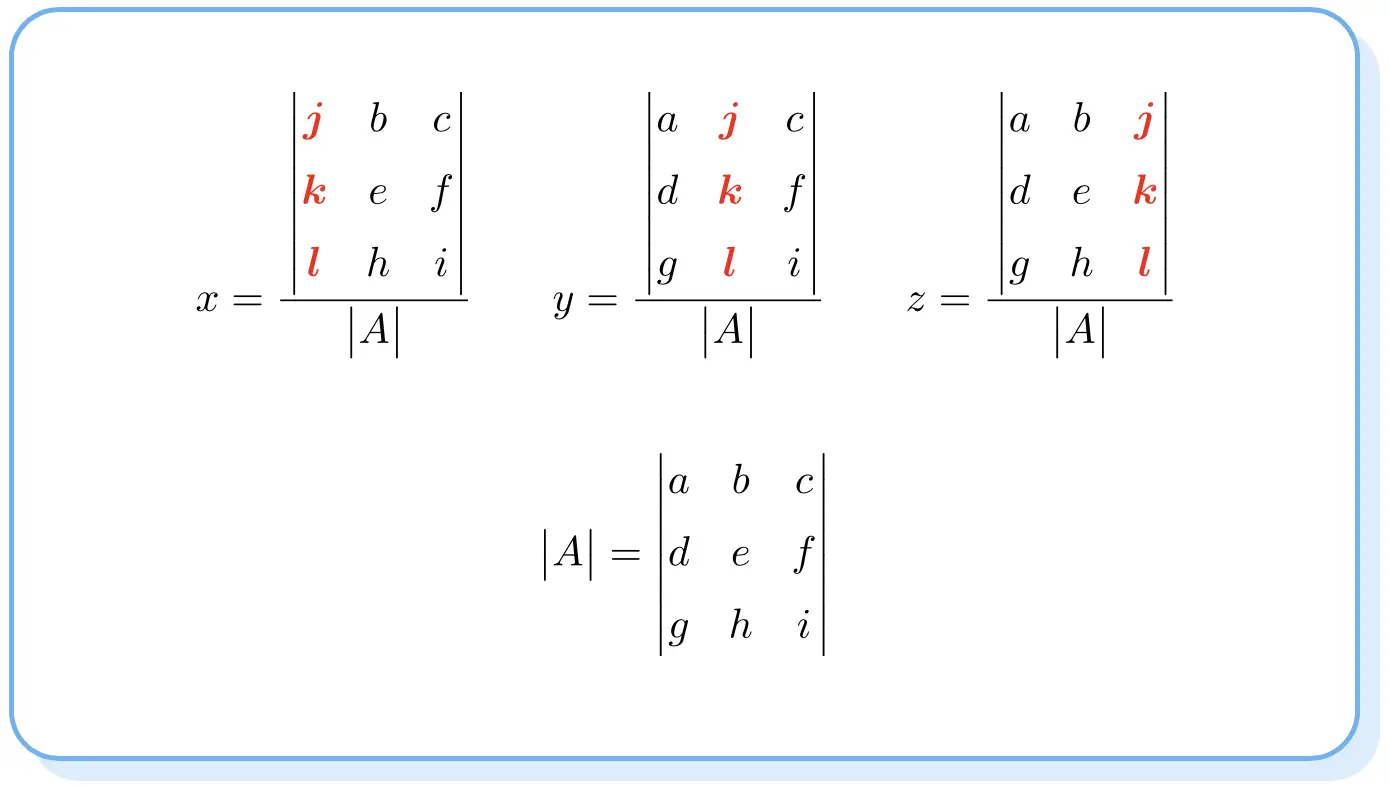
Обратите внимание, что определители числителей аналогичны определителям матрицы A, но столбец каждого неизвестного заменяется столбцом независимых членов.
Поэтому правило Крамера используется для решения систем линейных уравнений. Но, как вы уже знаете, существует множество способов решения системы уравнений, например хорошо известен метод Гаусса-Жордана .
Ниже приведены примеры решения систем линейных уравнений с помощью правила Крамера, которое иногда также записывают как правило Крамера.
Пример 1: определенная совместимая система (SCD)
- Решите следующую систему из трех уравнений с тремя неизвестными, используя правило Крамера:
![Rendered by QuickLaTeX.com \begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6013b7e73c89c24fe388f1a5d018f32b_l3.png)
Сначала мы создаем матрицу A и расширенную матрицу A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c710ed86223f47f39b5a25720b5ca19d_l3.png)
Теперь мы вычислим ранг двух матриц, чтобы увидеть, что это за система. Чтобы вычислить ранг A, мы вычисляем определитель 3 × 3 всей матрицы (используя правило Сарруса) и смотрим, дает ли он 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae4a3bb88d113494463df8e670c326c6_l3.png)
Определитель матрицы A отличен от 0, поэтому матрица A имеет ранг 3.
![]()
Таким образом , матрица A’ также имеет ранг 3 , поскольку она не может иметь ранг 4 и должна быть по крайней мере того же ранга, что и матрица A.
![]()
Размер матрицы А равен размеру матрицы А’ и числу неизвестных системы (3), поэтому по теореме Руше-Фробениуса мы знаем, что это детерминированная совместная система (ДСК):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
Как только мы узнаем, что система представляет собой SCD, мы применим правило Крамера для ее решения. Для этого напомним, что матрица А, ее определитель и матрица А’ равны:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b2b3e5865c2264c360fb887d37a5f6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a604d8f5a3927a47a264d28f7a007b2_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a1fa494ffb5e452d59c4d2dad40f925a_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера меняем второй столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08e3dabe2f33434eb96658491f67c0b4_l3.png)
Рассчитать
![]()
По правилу Крамера меняем третий столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96e76cb8867224755e9c19254678abd4_l3.png)
Таким образом, решение системы уравнений имеет вид:
![]()
Пример 2: Неопределенно совместимая система (ICS)
- Решите следующую систему уравнений, используя правило Крамера:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-781530aac4d8507fd6c7cbd77c3b4651_l3.png)
Сначала мы создаем матрицу A и расширенную матрицу A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a64800a78bf8e2e2f547be907e6863cb_l3.png)
Теперь мы вычисляем диапазон двух матриц и, таким образом, можем увидеть, что это за система. Чтобы вычислить ранг A, мы вычисляем определитель всей матрицы (используя правило Сарруса) и проверяем, равен ли он 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-581c58cbe0fdd9952e7e25b919ecc33b_l3.png)
Определитель дает 0, поэтому матрица A не имеет ранга 3. Но у нее есть определитель 2 × 2, отличный от 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Итак, матрица A имеет ранг 2 :
![]()
Как только мы узнаем размер матрицы A, мы вычисляем размер матрицы A’. Определитель первых трех столбцов дает 0, поэтому мы пробуем другие возможные определители 3×3 в матрице A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-686e7ca635ecee685005f6013c2e64ad_l3.png)
Все определители порядка 3 дают 0. Но, очевидно, матрица A’ имеет тот же определитель, отличный от 0 2×2, что и матрица A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5d1acad8bc31240f80d8cfbf3605997_l3.png)
Следовательно, матрица A’ также имеет ранг 2 :
![]()
Итак, поскольку ранг матрицы A равен рангу матрицы A’, но эти два меньше числа неизвестных системы (3), мы знаем по теореме Руше-Фробениуса , что это неопределенно совместимая система. (ИКС):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Когда мы хотим решить совместимую неопределенную систему (SCI), нам нужно преобразовать систему : сначала мы исключаем уравнение, затем преобразуем переменную в λ (обычно переменную z) и, наконец, помещаем члены с λ вместе с независимые термины.
После того, как мы преобразовали систему, мы применим правило Крамера и получим решение системы как функцию λ.
В этом случае исключим из системы последнее уравнение :
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0511fecc9c2af695b6b8eccae6b0661_l3.png)
Теперь преобразуем переменную z в λ:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d6142d2be611954fd849a032a97245a_l3.png)
И члены с λ ставим с независимыми членами:
![Rendered by QuickLaTeX.com \begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00214205f2334f1c9bc10810c1c1df83_l3.png)
Следовательно, матрица A и матрица A’ системы остаются:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c4b47303973b823a1c5628f5448ca79_l3.png)
Наконец, преобразовав систему, мы применяем правило Крамера . Поэтому решаем определитель A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b79f52dc82f5cfc311867273e78c06_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ff917eaea976c65bd18e0476078d3cb_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера меняем второй столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-155ca520739bbf7e040a6cdc632f7c27_l3.png)
А решение системы уравнений является функцией от λ, поскольку она является СКИ и, следовательно, имеет бесконечно много решений:
![]()
Правило Крамера решало проблемы
Упражнение 1
Примените правило Крамера для решения следующей системы двух уравнений с двумя неизвестными:
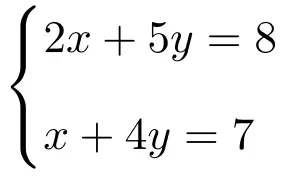
Первое, что нужно сделать, это матрица A и расширенная матрица A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a001db9cf56846150730fee7126dacd_l3.png)
Теперь мы должны найти ранг матрицы А. Для этого проверяем, отличен ли определитель всей матрицы от 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c75c1c344c286016bea83237f1f418e_l3.png)
Поскольку определитель матрицы 2×2 отличается от 0, матрица A имеет ранг 2:
![]()
Зная ранг A, мы вычисляем ранг A’. Это будет как минимум ранга 2, потому что мы только что видели, что внутри него есть определитель порядка 2, отличного от 0. Более того, он не может иметь ранга 3, поскольку мы не можем не создать определитель 3×3. Следовательно, матрица A’ также имеет ранг 2:
![]()
Следовательно, применяя теорему Руше-Фробениуса, мы знаем, что это совместимая детерминированная система (SCD), поскольку диапазон A равен диапазону A’ и числу неизвестных.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbd67b16bb6d52a0696e70a77833cd3b_l3.png)
Как только мы узнаем, что система представляет собой SCD, мы применим правило Крамера для ее решения.
Чтобы вычислить неизвестное
![]()
По правилу Крамера мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0adeda8f2ce557661466996038b1148_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера меняем второй столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-59790a66cc31fac07be1d5a7bb556d9e_l3.png)
Таким образом, решение системы уравнений имеет вид:
![]()
Упражнение 2
Найдите решение следующей системы трех уравнений с тремя неизвестными, используя правило Крамера:
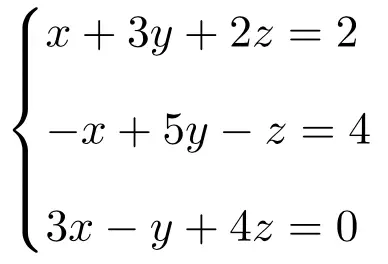
Сначала мы создаем матрицу A и расширенную матрицу A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-eea75fbf6d86ebc3d0b9e236cd2160f5_l3.png)
Теперь мы находим ранг матрицы A, вычисляя определитель матрицы 3×3 по правилу Сарруса:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-73f751f3b5c527c16b5de1b10bf07a4e_l3.png)
Матрица, имеющая определитель порядка 3, отличный от 0, матрица А имеет ранг 3:
![]()
следовательно, матрица A’ также имеет ранг 3:
![]()
Следовательно, используя теорему Руше-Фробениуса, мы знаем, что это совместимая детерминированная система (СКД), поскольку диапазон A равен диапазону A’ и числу неизвестных.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Как только мы узнаем, что система является SCD, нам нужно применить правило Крамера для решения системы.
Чтобы вычислить неизвестное
![]()
По правилу Крамера мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc574297f609b68e4fb48466ec6c8077_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера меняем второй столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2544601137d62e217ff1866f278203d6_l3.png)
Рассчитать
![]()
По правилу Крамера меняем третий столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42d7d4adcfc48954185ca14b56b8e128_l3.png)
Таким образом, решение системы уравнений имеет вид:
![]()
Упражнение 3
Рассчитайте решение следующей системы трех уравнений с тремя неизвестными, используя правило Крамера:
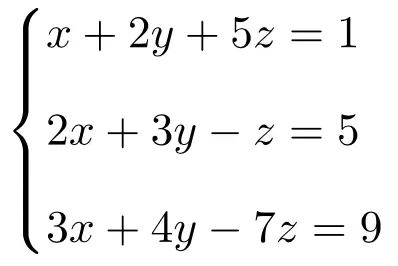
Сначала мы создаем матрицу A и расширенную матрицу A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-afd359275e5ebaaf3229504c47a5815f_l3.png)
Вычисляем размер матрицы A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ddf17a2b3eed5a680d685900a79b31_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdd4380c7c76418bd3ec12c94359f886_l3.png)
![]()
Как только мы узнаем размер матрицы A, мы вычисляем размер матрицы A’. Определитель первых трех столбцов дает 0, поэтому мы пробуем другие возможные определители 3×3 в матрице A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-1addc62130e0462075b3bade26a7e35e_l3.png)
Все определители порядка 3 дают 0. Однако матрица A’ имеет тот же определитель 2 × 2, отличный от 0, что и матрица A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-7de377466bd5afd03f58f9b532324e75_l3.png)
Следовательно, матрица A’ также имеет ранг 2:
![]()
Поскольку ранг матрицы A равен рангу матрицы A’, но эти два меньше числа неизвестных системы (3), по теореме Руше-Фробениуса мы знаем, что это неопределенная совместимая система (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Будучи системой ICS, мы должны исключить уравнение. В этом случае исключим из системы последнее уравнение :
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a1d067e155540f4345cf56e5c1567d3_l3.png)
Теперь преобразуем переменную z в λ:
![Rendered by QuickLaTeX.com \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5fa91777a722d3783b2f887aab44152_l3.png)
И члены с λ ставим с независимыми членами:
![Rendered by QuickLaTeX.com \begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76ff21181be050b01c247981298986a7_l3.png)
Такого, что матрица A и матрица A’ системы остаются:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-230e5b28dd467127e63f4f9756cf90da_l3.png)
Наконец, преобразовав систему, мы применяем правило Крамера . Поэтому решаем определитель A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1](https://mathority.org/wp-content/ql-cache/quicklatex.com-f127efbd217e2bca8852ec792610732f_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42652a14362b42e606841b6bb3e77cc0_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера меняем второй столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b95c5870f1762a2d82c9ebcccbca7408_l3.png)
А решение системы уравнений является функцией от λ, поскольку она является СКИ и, следовательно, имеет бесконечно много решений:
![]()
Упражнение 4
Решите следующую задачу о системе трех уравнений с тремя неизвестными, применив правило Крамера:
![Rendered by QuickLaTeX.com \begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e1c3458f33b863db10750b9e51d09e_l3.png)
Сначала построим матрицу A и расширенную матрицу A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-743a40010cb4a610e8a3fc6ae5d313b4_l3.png)
Теперь давайте вычислим ранг матрицы A, вычислив определитель матрицы 3×3 по правилу Сарруса:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-713c634fbc3e1b1cb228e3891c9bff1c_l3.png)
Матрица, имеющая определитель порядка 3, отличный от 0, матрица А имеет ранг 3:
![]()
следовательно, матрица A’ также имеет ранг 3, поскольку она должна быть по крайней мере того же ранга, что и матрица A, и не может иметь ранг 4, поскольку это матрица размерности 3×4.
![]()
Следовательно, используя теорему Руше-Фробениуса, мы приходим к выводу, что это детерминированная совместимая система (SCD), поскольку диапазон A равен диапазону A’ и числу неизвестных.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Как только мы узнаем, что система является SCD, нам нужно применить правило Крамера для решения системы.
Чтобы вычислить неизвестное
![]()
По правилу Крамера мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a290479c69ff806f19dcf29f96e1228_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера меняем второй столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bba0765fbcbcebf0585520af25b4a30_l3.png)
Рассчитать
![]()
По правилу Крамера меняем третий столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bc157a8c4dfe8ee4651affac68ef878_l3.png)
Таким образом, решение системы линейных уравнений имеет вид:
![]()
Упражнение 5
Решите следующую систему линейных уравнений, используя правило Крамера:
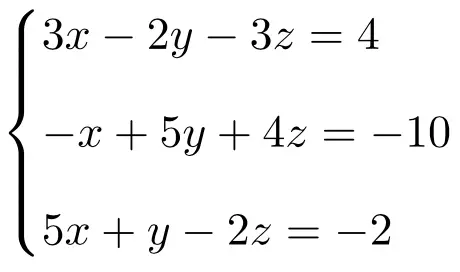
Сначала мы создаем матрицу A и расширенную матрицу A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5153b5951b768cc3cafa2bb2567ba92_l3.png)
Вычисляем размер матрицы A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3778c9499e2a44ea3834dfed1523163_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-03d70742b14ced92f33963df0c86e92f_l3.png)
![]()
Как только мы узнаем размер матрицы A, мы вычисляем размер матрицы A’. Определитель первых трех столбцов дает 0, поэтому мы пробуем другие возможные определители 3×3 в матрице A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bed93d532ae4ccd4649a73662f55f0f_l3.png)
Все определители порядка 3 дают 0. Но, очевидно, матрица А’ имеет тот же определитель порядка 2, отличный от 0, что и матрица А:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-858d95d7d252b16706b66c0e6aba09c4_l3.png)
Следовательно, матрица A’ также имеет ранг 2:
![]()
Ранг матрицы A равен рангу матрицы A’, но эти два меньше, чем количество неизвестных системы (3), поэтому по теореме Руше-Фробениуса мы знаем, что это неопределенная система, совместимая (SCI). :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Будучи системой ICS, мы должны исключить одно уравнение. В этом случае исключим из системы последнее уравнение :
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e10bd826663dff41c4272610cbc07b1_l3.png)
Теперь преобразуем переменную z в λ:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2502be450040b38761c08e5d6beaf379_l3.png)
И члены с λ ставим с независимыми членами:
![Rendered by QuickLaTeX.com \begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80a43d98e6be30965d554e8a89aa5d89_l3.png)
Такого, что матрица A и матрица A’ системы остаются:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3451ce571163983cf41794d4998283d6_l3.png)
Наконец, преобразовав систему, мы применяем правило Крамера . Поэтому решаем определитель A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e7a7d6208ea5e762f5c74a44e6838cf_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8c30fcc0526c2d4112eb4f60a3d8847f_l3.png)
Чтобы вычислить неизвестное
![]()
По правилу Крамера меняем второй столбец определителя А на столбец независимых членов и делим его на определитель А:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdb22a54274e019c811c9051502c474a_l3.png)
Таким образом, решение системы уравнений является функцией от λ, так как она является СКИ и, следовательно, система имеет бесконечно много решений:
![]()