На этой странице мы объясняем, как вычитать многочлены. Кроме того, вы найдете несколько примеров и решенных пошаговых упражнений на вычитание многочленов.
Как вычитать многочлены?
Чтобы вычесть два многочлена, необходимо вычесть члены полиномов, которые похожи. Другими словами, вычитание многочленов состоит из вычитания членов, имеющих одинаковую буквальную часть (те же переменные и одинаковые показатели степени).
В математике вычитание многочленов можно рассчитать двумя разными способами: вертикальным методом или горизонтальным методом. Ниже приводится объяснение обеих процедур, но мы советуем вам сначала научиться вычитать многочлены по вертикали, а затем переходить к горизонтальному методу. Очевидно, придерживайтесь того, который вы предпочитаете.
Вычитание вертикальных полиномов
Далее мы увидим, как два многочлена вычитаются по вертикали, на примере:
- сделать вычитание
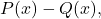
два полинома:
![]()
![]()
Первое, что нам нужно сделать, чтобы найти вычитание полинома, — это поместить один многочлен под другим так, чтобы одинаковые члены двух многочленов выровнялись в столбцах:
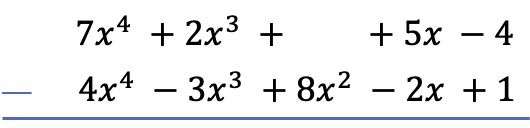
Внимание: если в полиноме нет члена определенной степени, место необходимо оставить пустым. Например, полином
![]()
не имеет квадратичного монома, поэтому на его месте стоит пустое место.
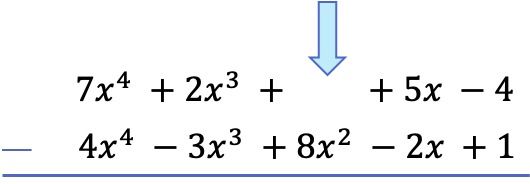
Хотя теперь мы можем вычитать многочлены напрямую, если мы поступим таким образом, очень легко ошибиться в знаке. Следовательно, чтобы вычесть многочлены, лучше всего изменить знак всех членов в вычитающем многочлене (вычитающем многочлене), а затем выполнить сложение. Поскольку вычитание многочлена — это то же самое, что добавление противоположного ему многочлена.
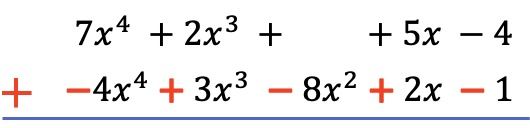
И как только мы расположили все члены в порядке от высшей степени к низшей и перевернули члены приведенного ниже многочлена, мы добавляем коэффициенты каждого столбца, сохраняя буквальные части равными:
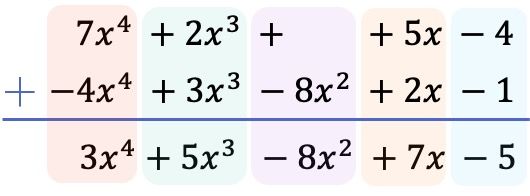
Таким образом, результат, полученный в результате вычитания двух полиномов:
![]()
Если последний шаг вам не ясен, я оставляю вам объяснение того, как происходит сложение многочленов , на самом деле важно, чтобы вы освоили сложение многочленов, чтобы иметь возможность успешно вычитать многочлены. На связанной странице вы также найдете примеры и решенные упражнения на сложение многочленов, а также сможете увидеть различия между сложением и вычитанием многочленов.
Вычитание горизонтальных полиномов
Мы только что увидели, как вычитать многочлены по вертикали, но теперь мы увидим другой метод вычитания многочленов: вычитание многочленов по горизонтали. Эта процедура, безусловно, быстрее предыдущей, однако необходимо хорошо владеть понятиями многочленов.
Итак, давайте посмотрим, в чем состоит этот метод вычитания многочленов на примере. И чтобы вы могли увидеть различия между двумя методами, мы будем вычитать те же полиномы, что и в предыдущем примере:
- Вычислить остаток
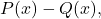
два полинома:
![]()
![]()
Сначала мы должны представить два многочлена в виде алгебраической операции, то есть один за другим:
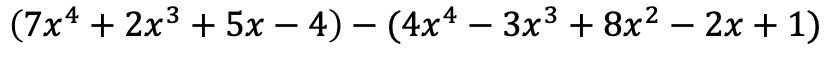
Одночлены в первой скобке остаются прежними, однако члены во второй скобке должны изменить знак, поскольку перед ними стоит отрицательный знак:
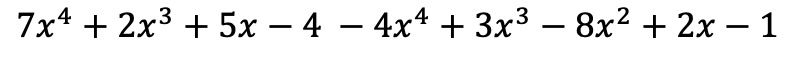
А теперь группируем термины, имеющие одинаковые литеральные части, то есть термины с одинаковыми переменными (буквами) и показателями. Несходные термины не могут быть добавлены или удалены.
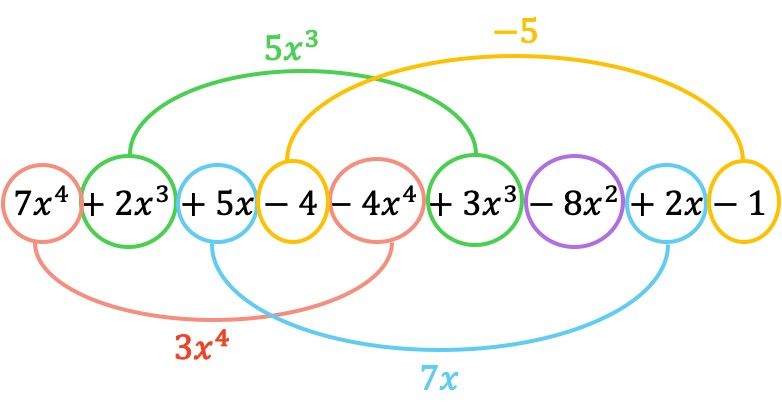
Таким образом, полином, полученный в результате вычитания, равен:
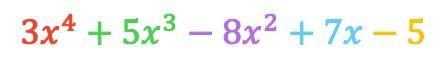
Как видите, мы получили одинаковый результат обоими методами, поэтому вы можете использовать тот, который вам больше подходит.
Теперь, когда вы познакомились с двумя методами решения вычитания многочленов, знаете ли вы, что вы также можете вычитать дроби с помощью многочленов? И не только вычитания, а всевозможные операции. Узнайте, как производятся действия с алгебраическими дробями , перейдя по этой ссылке.
Решенные задачи на вычитание многочленов
Чтобы вы могли попрактиковаться, мы оставляем вам несколько решенных упражнений на вычитание полинома. Если у вас есть вопросы по упражнению, вы можете задать их в комментариях на странице, мы ответим на них в ближайшее время.
Упражнение 1
Вычтите полином
![]()
минус полином
![]()
![]()
![]()
В этом случае мы вычтем два многочлена по вертикали. Для этого сначала упорядочим многочлены по степени, затем меняем знак у остальных полиномиальных членов и, наконец, сложим мономы, расположенные в одном столбце:
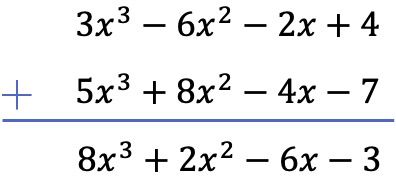
Упражнение 2
Решите полином вычитания
![]()
минус полином
![]()
![]()
![]()
Вычитание двух многочленов равнозначно добавлению противоположности вычитаемого многочлена к уменьшенному многочлену. Поэтому меняем знак членов субсжимающего полинома (оставшегося) и складываем полиномы:
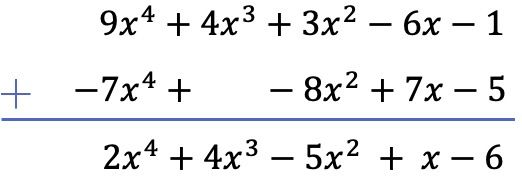
Обратите внимание, что в этом конкретном случае в столбце степени 3 второго многочлена необходимо оставить пустое место, поскольку в нем нет члена третьей степени.
Упражнение 3
Найдите результат вычитания многочлена
![]()
минус полином
![]()
![]()
![]()
В этом случае мы решим вычитание двух многочленов по вертикали. Итак, сначала расставляем многочлены в порядке от наибольшей к наименьшей степени, затем меняем знак членов оставшегося многочлена и, наконец, добавляем подобные слагаемые:
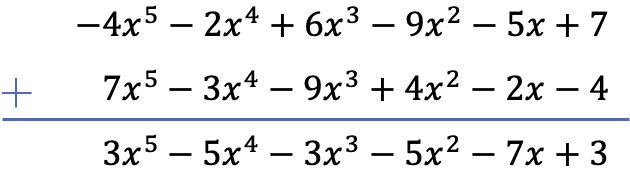
Упражнение 4
Вычислите следующую операцию с полиномами:
![]()
![]()
![]()
![]()
В данном случае в операции участвуют 3 многочлена, 2 из которых — вычитания. Поэтому для решения операции мы изменим знак всех членов двух оставшихся многочленов, а затем сложим многочлены.
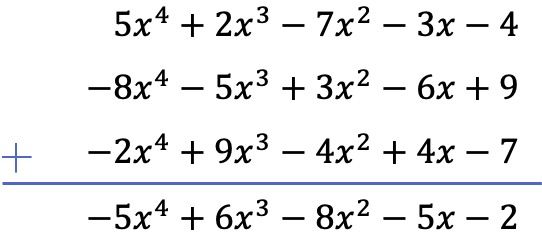
Что вы думаете об объяснении? Ты нашел это полезным? Какой метод вычитания многочленов вы предпочитаете: вертикальный или горизонтальный? Читаем вас в комментариях! 👀