Рациональная функция: что это такое, область определения, асимптоты, график, упражнения,...

Здесь вы узнаете, что такое рациональные функции. Кроме того, мы объясняем, как вычислить область определения и асимптоты рациональной функции. И не только это, вы увидите, каковы все характеристики рациональных функций. Наконец, вы можете попрактиковаться, выполняя пошаговые упражнения на рациональные функции.

Что такое рациональная функция?

Определение рациональной функции выглядит следующим образом:

Рациональная функция — это функция, образованная частным из двух многочленов , то есть рациональная функция — это дробь, имеющая многочлен в числителе и знаменателе.

Рациональные функции характеризуются особенностями в точках, где знаменатель обращается в нуль.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

Рациональные функции еще называют дробными функциями.

С другой стороны, не следует путать рациональные функции с иррациональными функциями. Иррациональные (или радикальные) функции – это те, которые состоят из корней.

Примеры рациональных функций

Чтобы лучше понять понятие рациональной функции, мы увидим несколько примеров функций этого типа.

Рациональная функция с полиномом первой степени в числителе и знаменателе:

$f(x)=\cfrac{x+3}{2x-5}$

Эти типы рациональных функций также называются функциями-омографами .

Рациональная функция с константой в числителе и многочленом в знаменателе:

$f(x)=\cfrac{7}{x+1}$

Эти типы рациональных функций называются обратными пропорциональными функциями и используются для математического определения обратно пропорциональных величин.

Рациональная функция с полиномом третьей степени в числителе и полиномом второй степени в знаменателе:

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

Область определения рациональной функции

Число, разделенное на 0, представляет собой неопределенность, которая дает бесконечность (∞), поэтому рациональная функция всегда будет существовать, если знаменатель не равен 0.

Следовательно, область определения рациональной функции состоит из всех действительных чисел, кроме значений, сокращающих знаменатель.

Итак, чтобы получить область определения рациональной функции, нам нужно найти, когда знаменатель равен 0, так как эта точка будет единственной, не принадлежащей области определения.

Давайте посмотрим, как вычисляется область определения рациональной функции, решив пример:

$f(x)=\cfrac{5x}{x+2}$

Сначала приравняем знаменатель к 0, затем решим полученное уравнение:

$x+2=0$

$x=-2$

Следовательно, когда x равен -2, знаменатель будет равен 0 и, следовательно, функция не будет существовать. Таким образом, область определения функции состоит из всех действительных чисел, кроме x=-2. Об этом говорится следующим образом:

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

Асимптоты рациональной функции

Одним из основных свойств рациональных функций являются их асимптоты, поскольку они определяют их графическое представление.

➤ См.: графическое представление функции.

Асимптоты рациональной функции — это линии, к которым график функции приближается бесконечно, но никогда не касается.

Существует три типа асимптот: вертикальные асимптоты, горизонтальные асимптоты и наклонные асимптоты.

Ниже представлены три типа асимптот, которые рациональная функция может изобразить красным цветом.

Вертикальная асимптота рациональной функции

Горизонтальная асимптота рациональной функции

Наклонная асимптота рациональной функции

Как видите, определить асимптоту функции по ее графику довольно просто, а вот вычислить асимптоты рациональной функции, не имея ее графического представления, достаточно сложно. Именно поэтому мы рекомендуем вам посмотреть, как вычисляются асимптоты функции, на нашем сайте.

Характеристики рациональной функции

Рациональные функции имеют следующие характеристики:

$f(x)=\cfrac{P(x)}{Q(x)}$

Как мы видели выше, в область определения рациональных функций входят все действительные числа, кроме значений, сокращающих знаменатель дроби.

Вообще, диапазон (или диапазон) рациональной функции включает в себя все действительные числа, кроме значений, в которых функция имеет горизонтальную асимптоту.

Рациональные функции непрерывны во всей своей области определения. Другими словами, рациональные функции демонстрируют разрывы в точках, не принадлежащих их области определения.

Графическое изображение большинства рациональных функций состоит из двух гипербол.

Некоторые правила для асимптот рациональных функций можно вывести из полиномиального числителя.
$P(x)$

и полином знаменателя

$Q(x):$
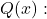
- Рациональная функция имеет вертикальную асимптоту в точках, являющихся корнями
  $Q(x)$
  
  но это не корни
  
  $P(x).$
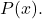
- Если степень
  $P(x)$
  
  меньше, чем степень
  
  $Q(x)$
  
  , линия y=0 является горизонтальной асимптотой рациональной функции.
- Если степень
  $P(x)$
  
  больше, чем степень
  
  $Q(x)$
  
  , рациональная функция не имеет горизонтальной асимптоты.
- Если степень
  $P(x)$
  
  является единицей, большей, чем степень
  
  $Q(x)$
  
  и два многочлена не имеют общего корня, рациональная функция имеет наклонную асимптоту.

Решенные упражнения на рациональные функции

Упражнение 1

Найдите область определения следующей рациональной функции:

$f(x)=\displaystyle\frac{4x}{2x+4}$

Посмотреть решение

Это рациональная функция, поэтому область определения состоит из всех чисел, кроме тех, которые сокращают знаменатель, поскольку тогда функция давала бы ∞.

Поэтому мы устанавливаем целочисленный знаменатель равным нулю, чтобы увидеть, какое число не принадлежит области определения:

$2x+4=0$

И решаем полученное уравнение:

$2x=-4$

$x=\cfrac{-4}{2}=-2$

Таким образом, область определения функции состоит только из чисел, кроме -2:

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

Упражнение 2

Найдите точки среза следующей рациональной функции с декартовыми осями:

$f(x)=\cfrac{x^2-9}{x}$

Посмотреть решение

Точка резки по оси X

Чтобы найти точку пересечения функции с осью X необходимо решить

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

Мы получили два решения квадратного уравнения, поэтому рациональная функция пересекает ось абсцисс в двух разных точках, а именно:

$\bm{(3,0)\qquad (-3,0)}$

Точка резки по оси Y

Чтобы найти точку пересечения с осью Y, необходимо вычислить

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

Любое число, разделенное на ноль, представляет собой неопределенность, дающую бесконечность. Следовательно, рациональная функция не проходит ни в одной точке выше оси Y, то есть не имеет точки пересечения с осью y.

Упражнение 3

Постройте на графике следующую рациональную функцию:

$y=\cfrac{2x+3}{2x+6}$

Посмотреть решение

Первое, что нужно сделать, это вычислить область определения функции:

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

Как только мы узнаем область определения функции, мы создадим таблицу значений:

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

В завершение просто изобразите полученные точки на графике и нарисуйте гиперболы, нарисовав таким образом рациональную функцию:

Упражнение 4

Определите асимптоты рациональной функции, изображенной на графике ниже:

Посмотреть решение

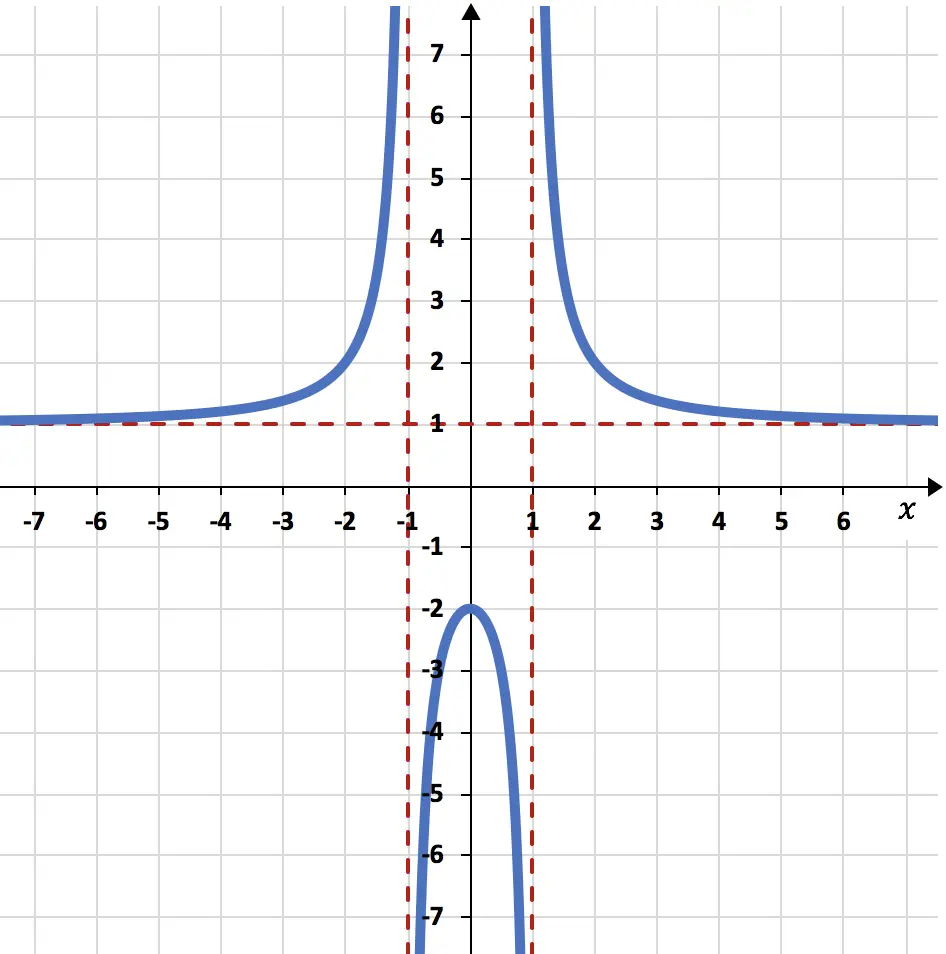
Асимптоты очень хорошо видны на графике, так как они представлены красными пунктирными линиями.

В этой задаче функция находится очень близко к горизонтальной линии y=1, но никогда не касается ее. Следовательно, рациональная функция имеет единственную горизонтальную асимптоту, которая равна y=1.

Аналогично, графическое представление функции очень близко к вертикальным линиям x=-1 и x=1, но никогда не достигает этих значений. Таким образом, рациональная функция имеет две разные вертикальные асимптоты: x=-1 и x=1.

Упражнение 5

Вычислите все асимптоты следующей рациональной функции:

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

Примечание. Для решения этого упражнения мы рекомендуем сначала перейти по ссылке выше о том , как вычисляются асимптоты функции, и посмотреть объяснение.

Посмотреть решение

вертикальная асимптота

Чтобы вычислить вертикальные асимптоты функции, мы должны сначала найти область определения функции. Поэтому положим знаменатель рациональной функции равным 0, чтобы найти точки, не принадлежащие области определения:

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

Таким образом, область определения функции состоит из всех чисел, кроме -1:

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

Таким образом, x=-1 может быть вертикальной асимптотой. Чтобы это проверить, надо вычислить предел функции в точке:

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

Следовательно, x=-1 является вертикальной асимптотой рациональной функции, поскольку предел функции в этой точке дает бесконечность.

горизонтальная асимптота

Для определения горизонтальных асимптот нам необходимо вычислить бесконечный предел функции:

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

В этом случае результатом неопределенного бесконечного предела между бесконечностью является деление коэффициентов при х высшей степени, так как числитель и знаменатель имеют один и тот же порядок.

Два бесконечных предела функции дали нам 3, поэтому y=3 — горизонтальная асимптота рациональной функции.

наклонная асимптота

Поскольку существует горизонтальная асимптота, рациональная функция не имеет наклонной асимптоты.

Что такое рациональная функция?

Примеры рациональных функций

Область определения рациональной функции

Асимптоты рациональной функции

Характеристики рациональной функции

Решенные упражнения на рациональные функции

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Оставьте комментарий Отменить ответ