▷ Как узнать, непрерывна ли функция (решенные упражнения)

В этой статье мы объясним, что такое непрерывные функции и как определить, непрерывна ли функция в точке или нет. Кроме того, вы найдете свойства непрерывных функций и анализ непрерывности наиболее распространенных функций. Наконец, вы можете попрактиковаться с решением упражнений на непрерывную функцию, чтобы полностью понять концепцию.

Что такое непрерывная функция?

Непрерывность функции можно изучить графически. Непрерывная функция — это функция, которую можно представить на графике, не отрывая карандаша от бумаги.

Непрерывная функция

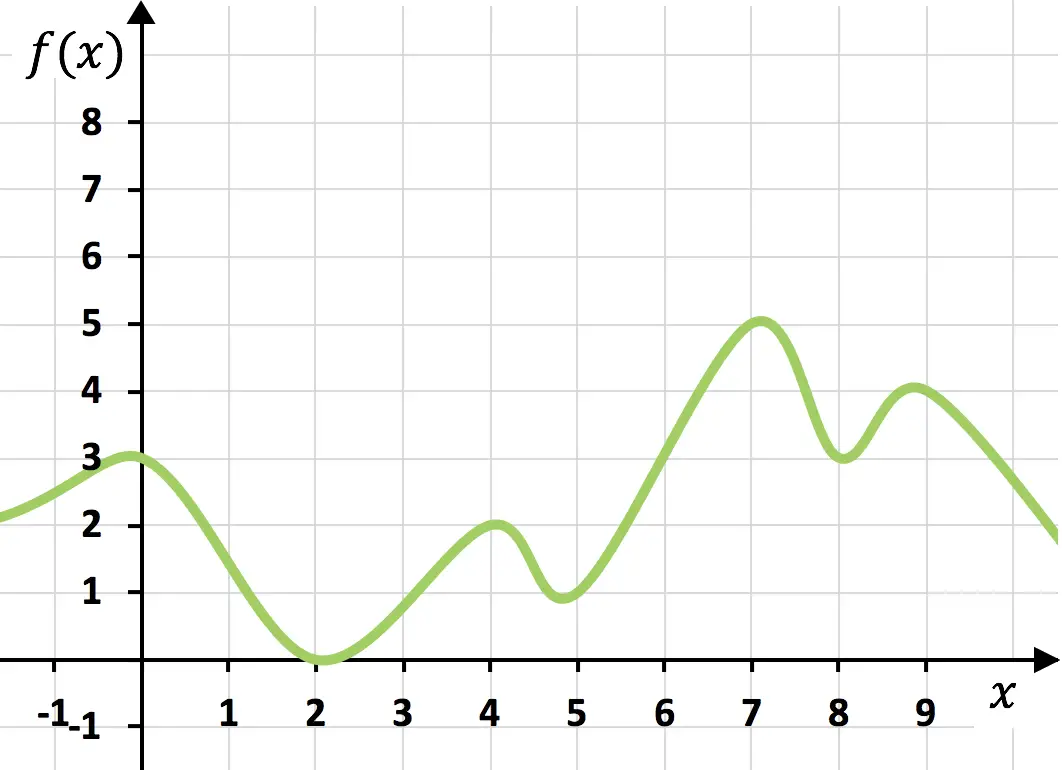
Вышеупомянутая функция является непрерывной, поскольку ее можно нарисовать одним мазком, не отрывая руки от бумаги.

С другой стороны, когда предыдущее условие непрерывности не ставится в функцию, она называется разрывной функцией .

Разрывная функция

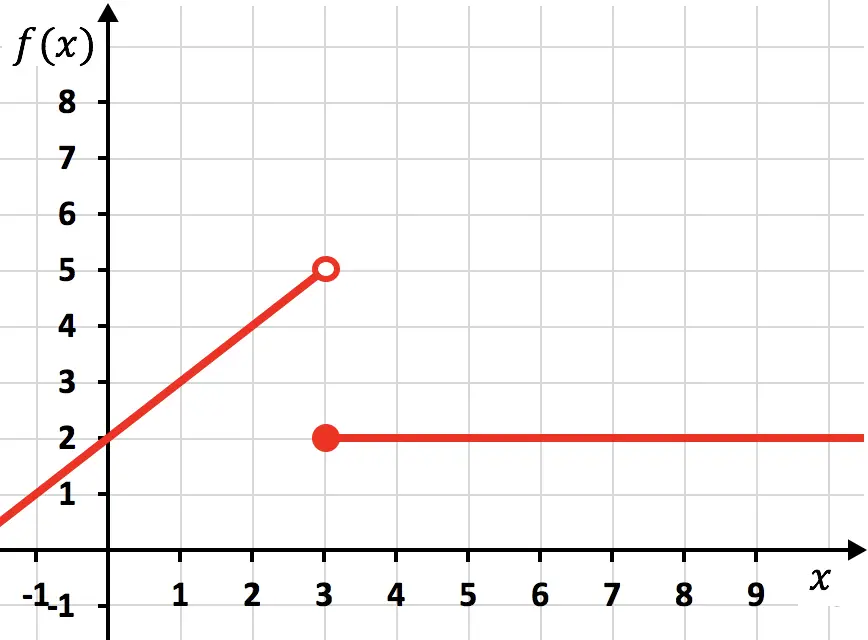
Предыдущая функция является разрывной, поскольку для ее представления необходимо провести карандашом две линии. В этом случае функция перестает быть непрерывной при x=3, поэтому мы говорим, что x=3 является точкой разрыва .

Кроме того, существует три типа разрывов : разрыв, которого можно избежать, разрыв с неизбежным конечным скачком и неизбежный разрыв с бесконечным скачком. По следующей ссылке вы можете увидеть, как выглядит каждый тип разрыва и чем он отличается:

➤ См.: виды разрывов

Непрерывность функции в точке

Как только мы увидим, как выглядит график непрерывной функции, мы посмотрим, как аналитически определить, является ли функция непрерывной или нет.

Математически функция непрерывна в точке, если выполняются следующие три условия:

Функция существует в этой точке, то есть существует образ точки.

$\exists \ f(a)$

На этом этапе существует предел функциональности. Следовательно, левый и правый боковые пределы функции в этой точке равны.

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

Образ точки совпадает с пределом функции в этой точке.

$\displaystyle f(a)=\lim_{x \to a} f(x)$

Таким образом, если три условия непрерывности выполняются во всех точках функции, функция непрерывна.

В качестве примера проанализируем непрерывность следующей кусочной функции:

непрерывность кусочно определенной функции

Даже если вы меняете разделы, в момент

$x=-2$

Функция непрерывна, так как боковые пределы функции в этой точке равны и в большей степени совпадают со значением функции в этой точке.

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

С другой стороны, функция не является непрерывной в точке

$x=4$

поскольку два боковых предела различны и, следовательно, предела функции в этой точке не существует:

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

Короче говоря, функция, определяемая кусочками, непрерывна во всех действительных числах, кроме

$x=4,$

где есть разрыв.

Мы также можем проверить, что функция разрывна в

$x=4$

потому что, чтобы изобразить это графически, необходимо в этом месте оторвать карандаш от бумаги.

Непрерывность элементарных функций

Некоторые типы функций непрерывны по своим характеристикам:

Постоянные функции непрерывны во всех действительных числах.

$f(x)=k$

Полиномиальные функции непрерывны для всех действительных чисел.

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Рациональные (или дробные) функции непрерывны во всех действительных числах, за исключением значений, которые сокращают знаменатель дроби, в этих точках функция представляет собой разрыв.

$f(x)=\cfrac{p(x)}{q(x)}$

Показательные функции непрерывны по всем действительным числам:

$f(x)=a^x$

Логарифмические функции непрерывны во всех точках, где их аргумент положителен.

$f(x)=\log_a (x)$

Непрерывность иррациональных функций , или функций с корнями, зависит от индекса радикала (n). Если индекс четный, это непрерывные функции во всех точках, которые делают корневой аргумент равным или больше нуля. Но если индекс нечетный, они являются непрерывными функциями всех действительных чисел.

$f(x)=\sqrt[n]{x}$

Непрерывность тригонометрических функций зависит от типа функции. Синус и косинус непрерывны на множестве действительных чисел, но касательная функция разрывна в точках
$\displaystyle x=\frac{\pi}{2}+k\pi$

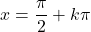
(где k — целое число).

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

Свойства непрерывных функций

Шон

$f(x)$

$g(x)$

две непрерывные функции в точке

$x=a,$

Сумма двух непрерывных функций в одной точке является другой непрерывной функцией в этой точке.

$f(x)+g(x)$

Произведение двух непрерывных функций в точке равно другой непрерывной функции в этой точке.

$f(x)\cdot g(x)$

Деление двух непрерывных функций в одной точке приводит к образованию другой непрерывной функции в этой точке, если эта точка не отменяет функцию деления.

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

Композиция двух непрерывных функций в одной точке порождает непрерывную функцию в этой же точке.

$f(x)\circ g(x)$

➤ Смотрите: что такое составная функция?

Решенные упражнения на непрерывность функции

Упражнение 1

Найдите разрывы функции, показанной на следующем графике. Также определите, какой это тип разрыва.

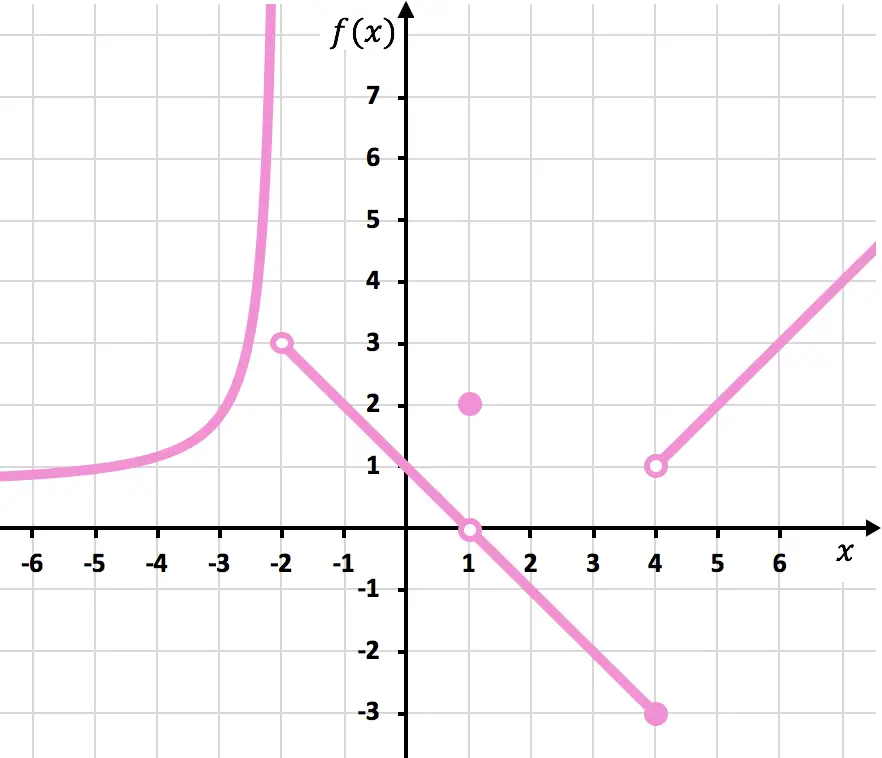
Примечание. Для выполнения этого упражнения мы рекомендуем сначала посмотреть, какие существуют типы разрывов и как они идентифицируются. Объяснение можно посмотреть по ссылке «Принцип типов разрывов» .

Посмотреть решение

Чтобы нарисовать функцию, необходимо поднять карандаш в точках x=-2, x=1 и x=4. Следовательно, функция разрывна в этих трех точках.

При x=-2 левый предел равен +∞, а правый предел равен 3. Таким образом, поскольку один из боковых пределов бесконечен, функция имеет неизбежный бесконечный скачок при x=-2.

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

Предел функции при x=1 равен 0, и, с другой стороны, значение функции при x=1 равно 2. Таким образом, функция представляет собой разрыв, которого можно избежать при x=1.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

При x = 4 левый предел равен -3, а правый предел равен 1. Следовательно, поскольку два боковых предела различны и ни один из них не дает бесконечности, функция неизбежно имеет конечный скачок при x = 4.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

Упражнение 2

Определите точки, в которых функция, показанная на следующем графике, становится разрывной.

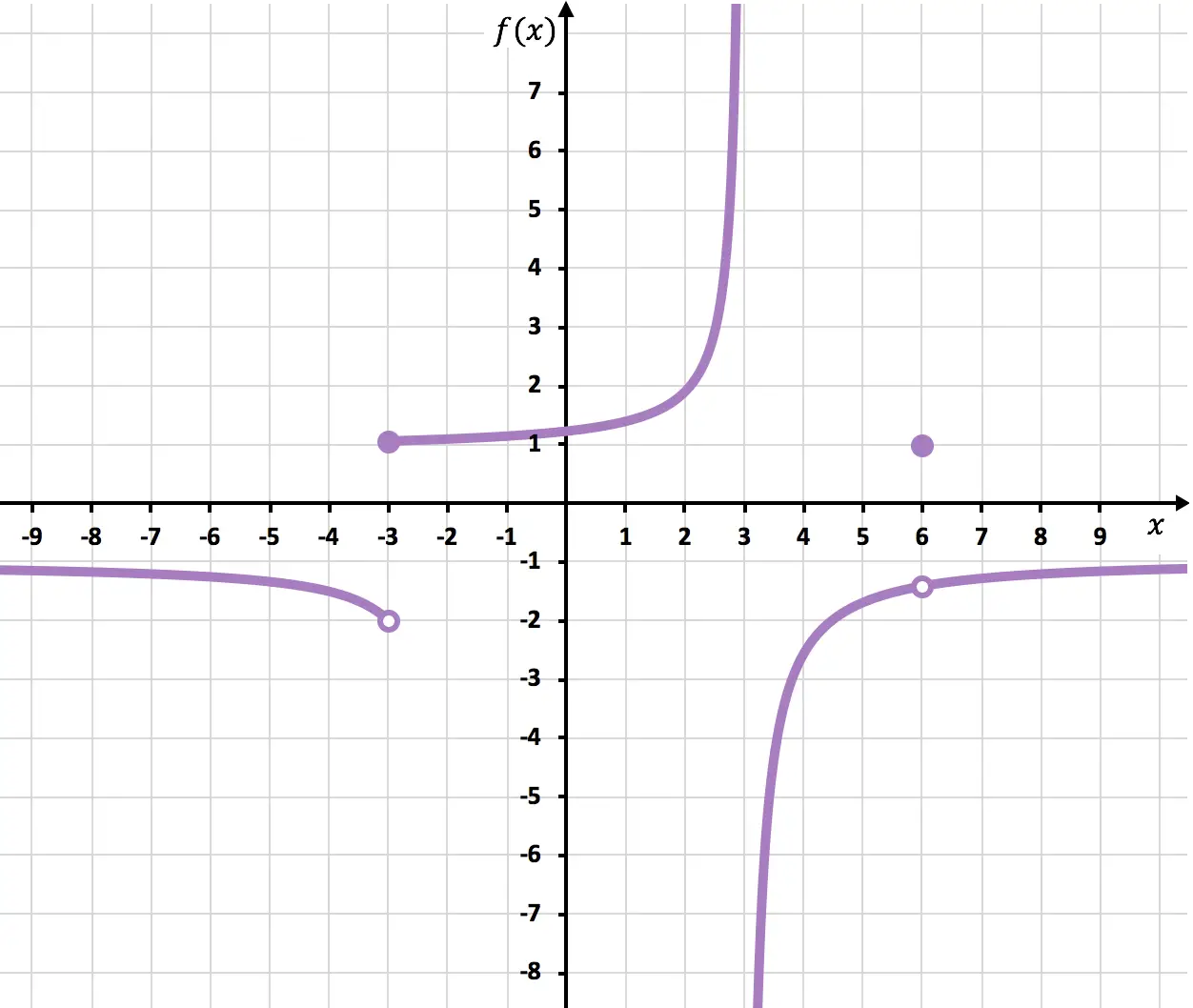
решаемое упражнение на типы разрывов функции

Посмотреть решение

В точке x=6 функция прерывается, поскольку имеется открытая точка. Предел при приближении x к 6 составляет -1,4, но f(6)=1. Таким образом, функция имеет разрыв, которого можно избежать при x=6, поскольку значение предела не совпадает со значением функции:

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

При x=-3 боковые пределы не совпадают и ни один из них не дает бесконечности. Таким образом, функция имеет неизбежный конечный скачок при x=-3.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

И, наконец, функция имеет неизбежный бесконечный скачок при x = 3, поскольку хотя бы один боковой предел в этой точке приводит к бесконечности.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Упражнение 3

Проанализируйте непрерывность следующей рациональной функции:

$\displaystyle f(x)= \frac{2}{x-5}$

Посмотреть решение

Рациональные функции непрерывны во всей своей области, то есть во всех действительных числах, кроме значений, которые сокращают знаменатель. Поэтому приравняем знаменатель рациональной функции нулю, чтобы увидеть, какие точки не принадлежат области определения:

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

Таким образом, функция будет непрерывной во всех точках, кроме x=5.

Упражнение 4

Проанализируйте непрерывность следующей кусочной функции:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

Посмотреть решение

Функция непрерывна и в первом разделе,

$5x-2$

, как и во втором разделе,

$x^2+2$

, поскольку они являются полиномиальными функциями.

Таким образом, единственная точка, в которой функция может быть разрывной, — это точка, в которой функция разбивается на куски. Итак, давайте посчитаем боковые пределы в этой точке:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

Таким образом, два боковых предела совпадают, предел функции при стремлении x к 1 равен 3:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

Более того, образ x=1 также равен 3:

$f(1)=1^2+2=\bm{3}$

Таким образом, поскольку предел функции в точке x=1 равен образу указанной точки, функция непрерывна в точке x=1. И поэтому оно непрерывно во всех действительных числах.

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

Упражнение 5

Изучите непрерывность следующей иррациональной функции:

$f(x)=\sqrt{2x+6}$

Посмотреть решение

Это радикальная функция с четным индексом, поэтому функция будет непрерывной до тех пор, пока аргумент радикала больше 0 (поскольку квадратный корень из отрицательного числа не существует):

$2x+6\ge 0$

Решаем неравенство:

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

Решение состоит из всех чисел, больших или равных -3. Таким образом, функция непрерывна на интервале своей области определения:

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

Упражнение 6

Проанализируйте непрерывность следующей логарифмической функции:

$f(x)=\log_3 (-3x+6)$

Посмотреть решение

Это логарифмическая функция, и не существует ни логарифма отрицательного числа, ни логарифма 0. Следовательно, функция будет существовать до тех пор, пока аргумент логарифма положителен (больше нуля):

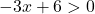$-3x+6>0″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»95″ style=»vertical-align: -2px;»> <p class=$ Решаем неравенство:

$-3x>-6″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»78″ style=»vertical-align: -2px;»> <p class=$ $x<\cfrac{-6}{-3}$

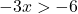
Помните, что когда вы делите отрицательное число на другую часть неравенства, вы должны поменять знак неравенства.

$x<2$

Решение состоит из всех чисел меньше 2. Таким образом, областью определения функции является:

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

Таким образом, функция непрерывна в каждой точке своей области определения.

Упражнение 7

Вычислите непрерывность следующей функции:

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

Посмотреть решение

В знаменателе дроби у нас есть радикал с четным индексом, поэтому функция будет существовать всякий раз, когда содержимое корня будет равно или больше нуля:

$-2x-8\geq 0$

Но также корень находится в знаменателе дроби, а знаменатель дроби никогда не может быть равен 0. Таким образом, функция будет существовать только в том случае, если содержимое корня строго больше 0:

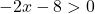$-2x-8> 0″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»95″ style=»vertical-align: -2px;»> <p class=$ Теперь решаем неравенство:

$-2x>8″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»64″ style=»vertical-align: -2px;»> <p class=$ $x<\cfrac{8}{-2}$

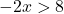
Помните, что когда мы меняем стороны отрицательного числа путем умножения или деления неравенства, мы также должны поворачивать знак неравенства.

$x<-4$

Результатом являются все числа меньше -4. Таким образом, область определения функции и, следовательно, ее непрерывность определяются следующим интервалом:

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

Упражнение 8

Вычислите значение k так, чтобы функция была непрерывной во всей

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.» title=»Rendered by QuickLaTeX.com» height=»65″ width=»225″ style=»vertical-align: 0px;»> <div class=$

Посмотреть решение

Чтобы функция была непрерывной, два боковых предела в точке излома должны давать одинаковый результат. Поэтому мы сначала вычисляем боковой предел в точке излома детали, которая не имеет k :

$\displaystyle \lim_{x \to 2^+} f(x) = \lim_{x \to 2} (3x^2 - 5) = 3\cdot 2^2-5=\bm{7}$

Следовательно, чтобы кусочная функция была непрерывной, другой предел также должен быть равен 7.

$\displaystyle \lim_{x \to 2^-} f(x) = \lim_{x \to 2} (kx-1) = k\cdot2 -1= 2k-1$

Таким образом, чтобы функция была непрерывной, два боковых предела любой точки должны давать один и тот же результат. Поэтому мы полагаем выражение, полученное из предела, равным 7 (результат другого латерального предела).