Здесь вы найдете формулы для всех типов уравнений линии. Кроме того, вы сможете увидеть примеры того, как они рассчитываются, а также потренироваться на решении упражнений уравнений прямой.
Каковы все уравнения прямой?
Помните, что математическое определение линии — это набор последовательных точек, которые представлены в одном направлении без кривых или углов.
Таким образом, для аналитического выражения любой прямой на плоскости (в R2) мы используем уравнения прямой, и для их нахождения достаточно точки, принадлежащей прямой, и вектора направления этой прямой. С помощью всего лишь этих двух геометрических элементов можно найти абсолютно все различные уравнения линии, а именно:
Уравнениями линии являются векторное уравнение, параметрические уравнения, непрерывное уравнение, неявное (или общее) уравнение, явное уравнение, уравнение наклона точки и каноническое (или сегментное) уравнение.
Все типы уравнений линий преследуют одну и ту же цель: математически представить линию. Но каждое уравнение линии имеет свои свойства и поэтому в зависимости от задачи лучше использовать то или другое.

Познакомившись с концепцией линейных уравнений, мы переходим к анализу характеристик каждого типа линейных уравнений в частности. Ниже вы найдете подробное объяснение различных типов уравнений в строке, но при желании вы можете перейти сразу к концу сводной таблицы с формулами всех уравнений в строке .
Векторное уравнение линии
Ага
![]()
— вектор направления линии и
![]()
точка, принадлежащая правому:
![]()
Формула векторного уравнения линии :
![]()
Золото:
-

И

— декартовы координаты любой точки на прямой.
-

И

— координаты известной точки, образующей часть линии

-

И

являются компонентами вектора направления прямой

-

— скаляр (действительное число), значение которого зависит от каждой точки прямой.
Это векторное уравнение прямой на плоскости, то есть при работе с точками и векторами 2-х координат (в R2). Однако если бы мы проводили расчеты в пространстве (в R3), нам пришлось бы добавить в уравнение линии дополнительную составляющую:
![]()
Параметрические уравнения линии
Параметрические уравнения линии можно получить из ее векторного уравнения:
![]()
Сначала умножаем параметр
![]()
вектором направления справа:
![]()
Далее мы добавляем координаты X и Y:
![]()
И, наконец, очистив каждую переменную отдельно, получим параметрические уравнения линии:
![]()
Золото:
-

И

— декартовы координаты любой точки на прямой.
-

И

— координаты известной точки, образующей часть линии

-

И

являются компонентами вектора направления прямой

-

— скаляр (действительное число), значение которого зависит от каждой точки прямой.
Как и раньше, это параметрические уравнения линии в плоскости (в R2), но для нахождения параметрических уравнений линии в пространстве (в R3) пришлось бы добавить еще одно уравнение для третьей переменной Z:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e31f05449ce57a8af9ae4dda38535013_l3.png)
Непрерывное уравнение линии
Непрерывное уравнение любой линии можно вывести из ее параметрических уравнений:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-708dbb33878e2bab0dcc94c84f6ab670_l3.png)
Если мы очистим настройку
![]()
из каждого параметрического уравнения получаем следующие выражения:
![]()
![]()
E Приравнивая два полученных уравнения, получаем непрерывное уравнение линии:
![]()
![]()
Короче говоря, непрерывное уравнение линии :
![]()
Золото:
-

И

— декартовы координаты любой точки на прямой.
-

И

— координаты известной точки, образующей часть линии

-

И

являются компонентами вектора направления прямой

Эта формула предназначена для непрерывного уравнения линии при работе в 2 измерениях (в 2D). Но если бы мы выполняли операции в трех измерениях (3D), нам нужно было бы добавить в уравнение линии дополнительный компонент:
![]()
Неявное или общее уравнение линии
Ага
![]()
— вектор направления линии и
![]()
точка, принадлежащая правому:
![]()
Формула неявного, общего или декартова уравнения линии :
![]()
Золото:
-

И

— декартовы координаты любой точки на прямой.
- коэффициент

– вторая составляющая вектора направления линии:

- коэффициент

– первая составляющая измененного знака вектора направления:

- коэффициент

рассчитывается путем замены известной точки

в уравнении прямой.
формулу неявного уравнения прямой можно получить и перемножением дробей непрерывного уравнения.
Явное уравнение линии
Формула явного уравнения линии :
![]()
Золото:
-

это наклон линии.
-

его точка пересечения по оси Y, то есть высота, на которой он пересекает ось Y.
В разделе ниже вы увидите, как определяются параметры.
![]()
И
![]()
прямой Но, в частности, другой способ найти явное уравнение — использовать неявное уравнение; для этого неизвестное должно быть решено
![]()
неявного уравнения.
Значение параметров m и n
Как мы видели при определении явного уравнения линии, параметр
![]()
это наклон линии и
![]()
это y-перехват. Но что это значит? Давайте посмотрим на это на графическом представлении линии:

Термин «независимый»
![]()
— точка пересечения линии с осью компьютера (ось OY). Например, на графике выше
![]()
равно 1, поскольку линия пересекает ось y в точке y=1.
С другой стороны, термин
![]()
указывает наклон линии , то есть ее наклон. Как вы видите на графике,
![]()
равно 2, так как линия поднимается на 2 единицы по вертикали за 1 единицу по горизонтали.
Очевидно, что если наклон положителен, функция возрастает (уходит вверх), а если наклон отрицательный, функция убывает (уменьшается).
Вычислить наклон линии
Как только мы точно узнаем, что такое наклон линии, давайте посмотрим, как он рассчитывается. Таким образом, существует 3 различных способа численного определения наклона линии:
- Даны две разные точки на прямой

И

Наклон линии равен:
- Ага

– вектор направления линии, ее наклон:
- Ага

— угол, образованный линией с осью абсцисс (ось X), наклон линии эквивалентен тангенсу указанного угла:
![]()
![]()
![]()

Уравнение точки-наклона линии
Формула уравнения точки-наклона линии :
![]()
Золото:
-

это наклон линии.
-

это координаты точки на прямой

Каноническое или сегментное уравнение линии
Хотя этот вариант уравнения линии менее известен, каноническое уравнение линии можно получить из точек пересечения линии с декартовыми осями.
Пусть две точки пересечения с осями данной прямой будут:
Разрезать по оси X:
![]()
Разрез по оси Y:
![]()
Формула канонического уравнения линии :
![]()

В математике каноническое уравнение прямой еще называют сегментным уравнением или симметричным уравнением.
С другой стороны, коэффициенты
![]()
И
![]()
Их также можно найти из общего уравнения линии по следующим формулам:
![]()
![]()
Все уравнения линии (формулы)
Вкратце, вот таблица, в которой показаны формулы всех уравнений линии:

Пример расчета уравнений линии
Теперь, когда мы увидели все объяснение уравнения прямой, давайте посмотрим, как решается типичная задача уравнений прямой:
- Найдите все уравнения прямой, определяемой точкой

и вектор
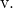
![]()
Прежде всего находим векторное уравнение линии по его формуле:
![]()
Просто подставьте координаты точки и вектора в формулу:
![]()
Во-вторых, находим параметрические уравнения линии через соответствующую ей формулу:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b4690a2ab033a4016f2d16b9554ddea_l3.png)
А еще определяем непрерывное уравнение линии по его формуле:
![]()
![]()
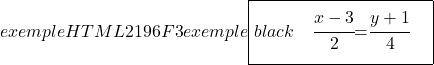
Как вы видели, векторные, параметрические и непрерывные уравнения легко вычислить, достаточно воспользоваться соответствующими формулами.
Перейдем теперь к нахождению общего (или неявного) уравнения линии. Для этого скрестим две дроби непрерывного уравнения:
![]()
![]()
![]()
![]()
Теперь мы можем определить явное уравнение решения прямой относительно неизвестной
![]()
неявного уравнения:
![]()
![]()
![]()
![]()
Следовательно, наклон линии равен 2 (слагаемое, сопровождающее независимую переменную
![]()
).
![]()
И благодаря этому мы можем вычислить уравнение наклона точки линии по его формуле:
![]()
![]()
![]()
Наконец, чтобы найти сегментное уравнение линии, мы вычисляем ее точки пересечения с осями OX и OY, а затем применяем его формулу:
![]()
Точка пересечения с осью абсцисс (ось X)
![]()
![]()
![]()
![]()
![]()
Точка пересечения с осью Y (ось Y)
![]()
![]()
![]()
![]()
![]()
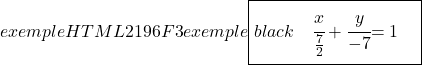
уравнение прямой, проходящей через две точки
Другая очень распространенная проблема в уравнениях линий — это нахождение уравнения линии, определяемой двумя заданными точками. Хотя мы можем рассчитать вектор направления линии с помощью двух точек, а затем уравнения, ниже мы предоставляем вам формулу, с помощью которой вы можете напрямую и легко найти уравнение указанной линии.
Рассмотрим две точки, расположенные на прямой:
![]()
Формула для нахождения уравнения линии по двум ее точкам :
![]()
Эта формула позволяет нам напрямую вычислить уравнение наклона точки для линии, когда нам даны 2 точки, через которые проходит линия.
Решенные задачи уравнений прямой
Упражнение 1
Найдите векторное уравнение, параметрические уравнения и непрерывное уравнение линии, определяемой точкой
![]()
и его направляющий вектор
![]()
Будьте обоими:
![]()
Сначала рассчитаем векторное уравнение линии по его формуле:
![]()
![]()
Затем находим параметрические уравнения линии, используя соответствующую формулу:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a734c32ae40ca816c19b895e54916eb4_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-bff16cf5ab85c87d8a866a2d74ea2a31_l3.png)
И, наконец, определяем непрерывное уравнение линии по соответствующей формуле:
![]()
![]()
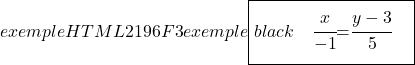
Упражнение 2
Найдите неявное уравнение, явное уравнение и уравнение наклона точки линии, определяемой точкой.
![]()
и его вектор направления равен
![]()
![]()
Формула неявного уравнения линии:
![]()
Поэтому мы должны найти коэффициенты A, B и C. Неизвестные A и B получаются из координат вектора направления прямой, поскольку всегда проверяется следующее равенство:
![]()
Следовательно, коэффициент А является второй координатой вектора, а коэффициент В — первой координатой вектора с измененным знаком:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9357fbcba6acde824f0fa1cc3e389a0c_l3.png)
Поэтому нам нужно найти только коэффициент C. Для этого мы должны подставить в ее уравнение точку, которая, как мы знаем, принадлежит прямой:
![]()
![]()
![]()
![]()
![]()
Итак, неявное, общее или декартово уравнение линии:
![]()
Теперь мы можем определить явное уравнение решения прямой относительно неизвестной
![]()
неявного уравнения:
![]()
![]()
![]()
![]()
Следовательно, наклон линии равен 3 (член перед независимой переменной
![]()
).
![]()
И по значению наклона линии мы можем вычислить уравнение наклона точки линии по его формуле:
![]()
![]()
![]()
Упражнение 3
Определите 3 точки на следующей линии, выраженные в виде неявного или общего уравнения:
![]()
Чтобы вычислить точку на линии, нам просто нужно присвоить значение одной из переменных, а затем найти значение другой переменной в этой точке.
Мы вычисляем первую точку, выполнив
![]()
![]()
![]()
![]()
![]()
![]()
Затем мы находим вторую точку, дающую другое значение переменной.
![]()
Например
![]()
![]()
![]()
![]()
![]()
![]()
![]()
И, наконец, вычисляем третью точку, решив
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Упражнение 4
Найдите все уравнения линии, определяемой точкой
![]()
и вектор
![]()
![]()
Прежде всего находим векторное уравнение линии по его формуле:
![]()
![]()
Во-вторых, находим параметрические уравнения линии через соответствующую ей формулу:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3bf46da9a68147118874a619f918077_l3.png)
А еще определяем непрерывное уравнение линии по его формуле:
![]()
![]()
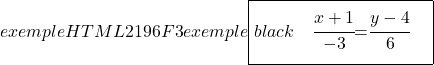
Перейдем теперь к нахождению неявного или общего уравнения линии. Для этого скрестим две дроби непрерывного уравнения:
![]()
![]()
![]()
![]()
Теперь мы можем определить явное уравнение решения прямой относительно неизвестной
![]()
неявного уравнения:
![]()
![]()
![]()
![]()
Следовательно, наклон линии эквивалентен -2 (член, который сопровождает независимую переменную
![]()
).
![]()
И благодаря этому мы можем вычислить уравнение наклона точки линии по его формуле:
![]()
![]()
![]()
Наконец, чтобы найти сегментное уравнение линии, вычисляем точки пересечения линии с осями OX и OY, затем используем его формулу:
![]()
Точка пересечения с осью абсцисс (ось X)
![]()
![]()
![]()
![]()
![]()
Точка пересечения с осью Y (ось Y)
![]()
![]()
![]()
![]()
![]()
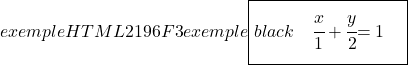
Упражнение 5
Найдите уравнение прямой, проходящей через следующие две точки:
![]()
Поскольку две точки на прямой нам уже известны, то непосредственно применим формулу уравнения прямой к 2 заданным точкам:
![]()
Теперь подставляем в формулу декартовы координаты точек:
![]()
И, наконец, вычисляем наклон линии:
![]()
![]()
Следовательно, уравнение линии, проходящей через эти две точки, имеет вид:
![]()