На этой странице вы узнаете, как рассчитывается расстояние между точкой и плоскостью в пространстве (формула). Кроме того, вы сможете увидеть примеры и попрактиковаться в упражнениях, решаемых шаг за шагом.
Чему равно расстояние от точки до плоскости?
В аналитической геометрии расстояние от точки до плоскости — это кратчайшее расстояние между этой точкой и любой другой точкой на плоскости. Это расстояние соответствует длине отрезка, перпендикулярного плоскости, идущего от точки к плоскости.

Формула расстояния от точки до плоскости
Как только мы в точности разобрались с понятием расстояния между точкой и плоскостью, давайте теперь посмотрим на формулу для расчета указанного расстояния:
Дана точка и общее (или неявное) уравнение плоскости:
![]()
Формула расстояния от точки до плоскости :
![]()
Доказательство формулы расстояния от точки до плоскости довольно утомительное и долгое, поэтому на этой странице мы его делать не будем.
С другой стороны, если при применении формулы мы получим результат, равный нулю, это, очевидно, означает, что расстояние между точкой и плоскостью равно нулю и, следовательно, точка является частью этой плоскости.
Наконец, обратите внимание, что для применения формулы план должен быть определен как общее (или неявное) уравнение. Поэтому, если бы оно было выражено уравнением плоскости другого типа, нам пришлось бы сначала преобразовать его в общее уравнение, а затем использовать формулу.
Пример расчета расстояния от точки до плоскости
Чтобы вы могли увидеть, как численно определяется расстояние между точкой и плоскостью, решим пример ниже:
- Вычислите расстояние между точкой P и плоскостью π. Сказав точку и план:
![]()
Чтобы найти расстояние от точки до плоскости, просто примените формулу, приведенную в разделе выше:
![]()
Теперь подставим значение каждого неизвестного в формулу:
![]()
И, наконец, делаем операции:
![]()
![]()
Обратите внимание, что в числителе дроби стоит абсолютная величина, а в знаменателе у нас квадратный корень, поэтому результат всегда должен быть положительным. Это имеет смысл, поскольку расстояния не могут быть отрицательными, но всегда положительны.
Вычислить расстояние между двумя параллельными плоскостями
Две параллельные плоскости всегда находятся на одинаковом расстоянии, поэтому, чтобы найти расстояние между двумя параллельными плоскостями, мы можем взять точку на одной из двух плоскостей и вычислить расстояние от этой точки до другой плоскости.

Это метод определения расстояния между двумя параллельными плоскостями. Однако есть еще более простой способ сделать это, когда коэффициенты А, В и С уравнений двух плоскостей совпадают:
Рассмотрим общие (или неявные) уравнения двух параллельных плоскостей:
![]()
Формула расчета расстояния между двумя параллельными плоскостями :
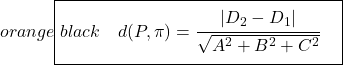
Так что, конечно, легче найти расстояние между двумя параллельными плоскостями, используя формулу, поскольку это всего лишь вопрос применения формулы и все, но это зависит от задачи. Кроме того, мы считаем, что лучше объяснить оба способа расчета расстояния, чтобы вы могли выбрать тот, который вам больше нравится.
Пример расчета расстояния между двумя параллельными плоскостями
В качестве примера мы рассчитаем расстояние между следующими двумя плоскостями:
![]()
Сначала мы должны убедиться, что мы имеем дело с двумя параллельными плоскостями. Таким образом, все коэффициенты уравнений плоскости пропорциональны, за исключением независимых членов, поэтому фактически они представляют собой две параллельные плоскости.
![]()
В этом случае члены А, В и С уравнений двух плоскостей не совпадают, но добиться этого можно, разделив все уравнение второй плоскости на два:
![]()
![]()
Итак, уравнения двух плоскостей уже имеют одинаковые коэффициенты A, B и C. Поэтому мы легко можем вычислить расстояние между двумя плоскостями по формуле расстояния между двумя параллельными плоскостями:
![]()
Подставляем значения и решаем операции:
![]()
Так что расстояние между одной плоскостью и другой плоскостью равно единице.
Решение задач о расстоянии от точки до плоскости
Упражнение 1
Вычислите расстояние между точкой P и плоскостью, декартово (или общее) уравнение которой имеет вид:
![]()
Чтобы рассчитать расстояние от точки до плоскости, необходимо воспользоваться соответствующей формулой:
![]()
Подставляем значение каждого параметра в формулу:
![]()
И, наконец, делаем операции:
![]()
![]()
![]()
Упражнение 2
Найдите расстояние между точкой P и плоскостью π:
![]()
Прежде чем использовать формулу расстояния от точки до плоскости, необходимо сначала выразить плоскость в виде неявного (или общего) уравнения:
![]()
И теперь мы можем воспользоваться формулой для определения расстояния от точки до плоскости:
![]()
Подставляем значение каждого слагаемого в формулу:
![]()
И, наконец, выполняем операции:
![]()
![]()
Упражнение 3
Используя формулу расстояния между точкой и плоскостью, определите, лежит ли точка P в плоскости π.
![]()
Чтобы проверить, принадлежит ли точка плоскости, мы можем вычислить расстояние между ними: если расстояние равно нулю, это означает, что точка действительно принадлежит плоскости, с другой стороны, если расстояние отличается от 0, это означает, что точка принадлежит плоскости. точка находится вне плоскости. план.
Поэтому расстояние между точкой и плоскостью определяем по формуле:
![]()
![]()
![]()
![]()
![]()
Расстояние между точкой и плоскостью эквивалентно нулю, поэтому точка фактически принадлежит плоскости.
Упражнение 4
Найдите расстояние между следующими двумя плоскостями:
![]()
Сначала мы должны убедиться, что мы имеем дело с двумя параллельными плоскостями. Все коэффициенты уравнений двух плоскостей пропорциональны, за исключением независимых членов, так что это действительно две параллельные плоскости.
![]()
В этом случае расстояние между двумя плоскостями мы рассчитаем по формуле, так как их коэффициенты A, B и C равны:
![]()
Итак, подставляем значения в формулу и выполняем операции:
![]()
Упражнение 5
Найдите расстояние между следующими двумя параллельными плоскостями:
![Rendered by QuickLaTeX.com \pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-6d14719b0eefd313552d5257c249c66f_l3.png)
Плоскость переднего плана определяется в виде параметрических уравнений, поэтому, чтобы применить формулу для расстояния между двумя параллельными плоскостями, нам нужно сначала преобразовать ее в форму общего уравнения, а это требует много вычислений и времени. Следовательно, будет быстрее, если мы возьмем точку на этой плоскости и вычислим расстояние от этой точки до другой плоскости.
Таким образом, координаты точки, через которую проходит плоскость π 1 , соответствуют независимым членам каждого параметрического уравнения:
![]()
Теперь применим формулу, чтобы найти расстояние между этой точкой и другой плоскостью:
![]()
![]()
![]()
![]()
![]()
Следовательно, расстояние между двумя параллельными плоскостями равно:
![]()