На этой странице вы узнаете, что такое параметрические уравнения плана и как они рассчитываются (формулы). Кроме того, вы сможете увидеть примеры и попрактиковаться в упражнениях, решаемых шаг за шагом.
Что такое параметрические уравнения плоскости?
В аналитической геометрии параметрические уравнения плоскости — это уравнения, которые позволяют математически выразить любую плоскость. Чтобы найти параметрические уравнения плоскости, нам нужна только точка и два линейно независимых вектора, принадлежащих этой плоскости.
Формулировка параметрических уравнений плана
Рассмотрим точку и два направляющих вектора плоскости:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Формула параметрического уравнения плоскости :
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f74da212d3f5f1c3a3002d71a4bed96_l3.png)
Золото
![]()
И
![]()
два скаляра, то есть два действительных числа.
Важно, что два направляющих вектора уравнения плоскости линейно независимы, то есть имеют разное (непараллельное) направление. В противном случае приведенное выше уравнение не представляло бы никакого плана.

С другой стороны, имейте в виду, что помимо параметрического уравнения существуют и другие способы аналитического выражения плоскости в пространстве (в R3), например общее уравнение плоскости . По этой ссылке вы найдете его формулу, как она рассчитывается из параметрических уравнений плана, примеры и решенные упражнения.
Пример того, как найти параметрические уравнения плоскости
Раз мы увидели, что такое параметрическое уравнение плоскости, давайте посмотрим, как оно рассчитывается на примере:
- Найдите параметрические уравнения плоскости, проходящей через точку
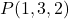
и содержит векторы
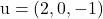
И
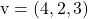
Для определения параметрических уравнений плана достаточно применить его формулу:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46f87775f11f01a59c70aa3ee864aebe_l3.png)
А теперь подставим точку и каждый вектор направления в уравнение:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-501ec8b26b4d88ebe95abd3ca7e7fe44_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e8517084217ee5519c428b598f2d7f8_l3.png)
Как перейти от векторного уравнения плоскости к параметрическим уравнениям
Другой метод определения параметрических уравнений плоскости — из векторного уравнения плоскости. Ниже вы можете увидеть демо.
Пусть векторное уравнение любой плоскости имеет вид:
![]()
Оперируем и сначала осуществляем произведения векторов на скаляры:
![]()
Далее добавляем компоненты:
![]()
И, наконец, получим параметрическое уравнение плоскости, усвоив координаты, соответствующие каждой переменной в отдельности:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46f87775f11f01a59c70aa3ee864aebe_l3.png)
Как видно из двух приведенных выше примеров, найти параметрические уравнения плоскости относительно легко. Однако задачи могут немного усложниться, поэтому ниже вы найдете несколько решенных упражнений разной сложности, чтобы вы могли попрактиковаться.
Решенные задачи параметрических уравнений плоскости
Упражнение 1
Определить параметрические уравнения плоскости, содержащей вектор
![]()
и проходит через следующие два пункта:
![]()
И
![]()
Чтобы узнать уравнение плоскости, вам нужна точка и два вектора, и в этом случае у нас есть только один вектор, поэтому мы должны найти другой направляющий вектор плоскости. Для этого мы можем вычислить вектор, который определяет две точки плоскости:
![]()
Теперь, когда мы уже знаем два направляющих вектора плоскости и точки, поэтому воспользуемся формулой параметрических уравнений плоскости:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
И подставим в уравнение два вектора и одну из двух точек плоскости:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ecedfca92c24d2754bcca977f2f30e76_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c67219e6157433f05d410c0aefb05f05_l3.png)
Упражнение 2
Найдите параметрические уравнения плоскости, содержащей следующие три точки:
![]()
Чтобы найти параметрические уравнения плоскости, нам нужно найти два линейно независимых вектора, которые соединяются в плоскости. И для этого мы можем вычислить два вектора, которые определяются тремя точками:
![]()
![]()
Координаты двух найденных векторов не пропорциональны, поэтому линейно независимы друг от друга.
Теперь, когда мы уже знаем два направляющих вектора и точку на плоскости, применим формулу параметрического уравнения плоскости:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
И подставляем в уравнение два вектора и одну из трёх точек плоскости:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
Упражнение 3
Вычислите параметрические уравнения плоскости, определяемые следующим векторным уравнением:
![]()
Чтобы преобразовать векторное уравнение плоскости в параметрическое уравнение, необходимо оперировать координатами, а затем решать каждую переменную отдельно:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-381b1ceea87f332904ae69a566ecd1af_l3.png)
Упражнение 4
Найдите параметрические уравнения плоскости, содержащей прямую
![]()
и параллельно вправо
![]()
это строки:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
Чтобы найти параметрические уравнения плоскости, нам нужно знать два вектора направления и точку на плоскости. Инструкция сообщает нам, что она содержит строку
![]()
Следовательно, мы можем взять вектор направления и точку на этой линии, чтобы определить плоскость. Более того, это утверждение говорит нам, что плоскость параллельна прямой.
![]()
поэтому мы также можем использовать вектор направления этой линии для уравнения плоскости.
право
![]()
выражается в виде параметрических уравнений, поэтому компонентами его вектора направления являются коэффициенты при параметрических членах
![]()
![]()
А декартовы координаты точки на этой же прямой являются независимыми членами параметрических уравнений:
![]()
С другой стороны, прямая линия
![]()
представляет собой непрерывное уравнение, такое, что компоненты его вектора направления являются знаменателями дробей:
![]()
Следовательно, параметрические уравнения плана имеют вид:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)