На этой странице объясняются различные относительные положения, существующие между линией и кругом. Кроме того, вы сможете увидеть, как найти относительное положение между линией и кругом.
Каково взаимное расположение линии и окружности?
В аналитической геометрии относительное положение линии по отношению к окружности может быть только внешним, касательным или секущим:
- Внешний : когда расстояние между линией и центром круга больше радиуса.
- Касательная : когда расстояние между линией и центром круга равно радиусу.
- Секанс : когда расстояние между линией и центром круга меньше радиуса.
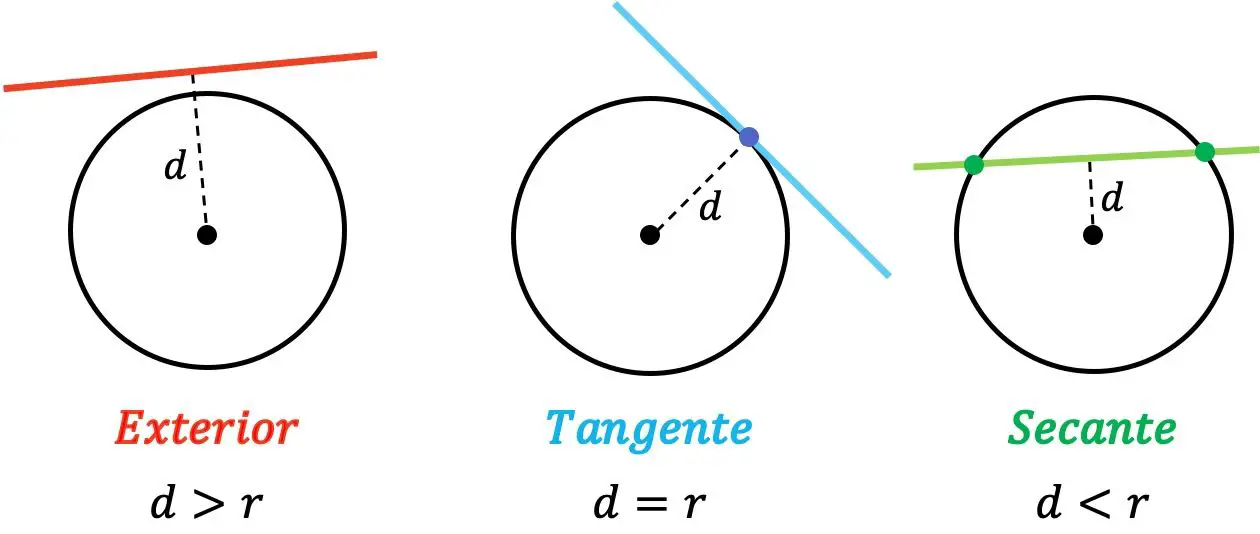
Итак, если линия находится вне круга, она не пересекает его ни в одной точке. С другой стороны, когда линия касается окружности, у них есть общая точка. И, наконец, прямая является секущей окружности, если она пересекает ее в двух разных точках.
Как определить относительное положение линии и круга?
Существует два способа найти относительное положение прямой относительно окружности на плоскости: один путем вычисления расстояния между линией и центром круга, а другой путем решения сложной системы уравнений уравнения линия и уравнение окружности.
Далее мы посмотрим, что представляет собой каждый метод.
Способ 1: Расстояние между линией и центром круга.
Как мы видели в объяснении понятия относительного положения между линией и кругом, расстояние между линией и центром круга указывает, какой это тип относительного положения.
Таким образом, этот метод заключается в нахождении расстояния между линией и центром круга. Очевидно, что для того, чтобы это сделать, вы должны знать , как рассчитать расстояние между точкой и линией . На этой странице вы можете увидеть, как это сделать, а также примеры и решенные упражнения для практики.
Итак, в зависимости от полученного результата расстояния будет тот или иной случай:
- Линия окажется вне круга, если полученное расстояние больше радиуса круга.
- Линия будет касательной к окружности, если полученное расстояние эквивалентно радиусу окружности.
- Линия пересечет круг, если полученное расстояние меньше радиуса круга.
Способ 2: решить систему уравнений
Другой способ найти относительное положение прямой к окружности — использовать систему уравнений, образованную уравнением прямой и уравнением окружности. Очевидно, что для применения этого метода нужно знать , что такое уравнение окружности и какова формула уравнения прямой .
В зависимости от количества решений системы уравнений мы столкнемся с тем или иным случаем:
- Если система уравнений не имеет решения, это означает, что прямая и окружность не имеют общей точки, поэтому прямая находится вне окружности.
- Если система уравнений имеет 1 решение, это означает, что прямая и окружность имеют общую точку, следовательно, прямая касается окружности.
- Если система уравнений имеет 2 решения, это означает, что прямая и окружность имеют две общие точки, следовательно, прямая секущая окружности.