Здесь вы узнаете, как рассчитывается уравнение (формула) эллипса, независимо от того, имеет ли оно начало координат в центре или нет. Вы также узнаете, что такое элементы эллипса, как их рассчитать и для чего они используются. Кроме того, вы сможете увидеть примеры и решения уравнений эллипса.
Формула уравнения эллипса
Формула уравнения эллипса в декартовых координатах:
![]()
Золото:
-

И

– координаты центра эллипса:
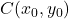
-

— горизонтальный радиус эллипса.
-

— вертикальный радиус эллипса.
Уравнение эллипса с центром в начале координат
Очень распространенный тип эллипса — это тот, центр которого находится в начале координат, то есть в точке (0,0). Вот почему мы увидим, как найти уравнение эллипса с центром в начале координат.
Следуя формуле уравнения эллипса:
![]()
Если эллипс центрирован в начале координат, это означает, что
![]()
И
![]()
равны 0, поэтому ваше уравнение будет:
![]()
Некоторые математики также называют это выражение каноническим уравнением или приведенным уравнением эллипса.
элементы эллипса
Как только мы увидим, как выглядит уравнение эллипса, мы увидим, каковы его элементы. Но сначала давайте вспомним, что такое эллипс:
Эллипс представляет собой плоскую замкнутую изогнутую линию, очень похожую на окружность, но по форме более овальную. В частности, эллипс — это геометрическое место всех точек плоскости, сумма расстояний которых до двух других фиксированных точек (называемых фокусами F и F’) постоянна.
Итак, элементами эллипса являются:
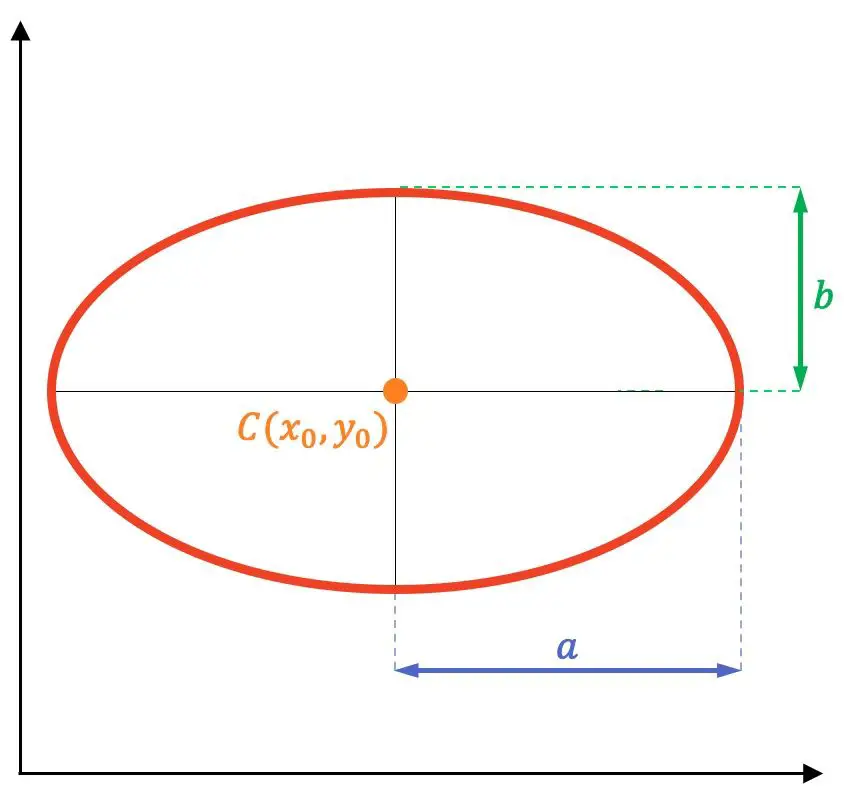
- Фокусы : это фиксированные точки F и F’ (точки фиолетового цвета на изображении ниже). Сумма расстояний между любой точкой эллипса и каждым фокусом постоянна для всех точек эллипса.
- Главная или фокальная ось : это ось симметрии эллипса, в котором расположены фокусы. Также называется главной осью.
- Вторичная ось : это ось симметрии эллипса, перпендикулярная главной оси. Ее еще называют малой осью и она соответствует биссектрисе сегмента, соединяющего фокусы.
- Центр : точка пересечения осей эллипса. Кроме того, это центр симметрии эллипса (оранжевая точка на графике).
- Вершины : точки пересечения эллипса с его осями симметрии (черные точки).
- Большая полуось или главная ось: отрезок, идущий от центра эллипса к вершинам главной оси.
- Малая полуось или вторичная ось: сегмент между центром эллипса и вершинами вторичной оси.
- Фокусное расстояние : это расстояние между двумя фокусными точками.
- Полуфокусное расстояние : соответствует расстоянию между центром и каждой из фокусных точек.
- Радиовекторы : сегменты, которые соединяют любую точку эллипса с каждым фокусом (синие сегменты на графике).

Связь между элементами эллипса
Различные элементы эллипса связаны друг с другом. Кроме того, связи между ними очень важны для упражнений на эллипсах, поскольку они обычно необходимы для решения задач на эллипсах и определения их уравнений.
Как мы видели выше в определении эллипса, расстояние от любой точки эллипса до фокуса F плюс расстояние от той же точки до фокуса F’ является постоянным. Что ж, это постоянное значение в два раза больше, чем измеряет большая полуось. Другими словами, для любой точки эллипса справедливо следующее равенство:
![]()
Золото
![]()
И
![]()
— расстояние от точки P до фокуса F и F’ соответственно и
![]()
– длина полуфокальной оси.
Следовательно, поскольку вершина вторичной оси находится как раз посередине фокальной оси, расстояние от нее до одного из фокусов эквивалентно длине полупервичной оси (
![]()
):
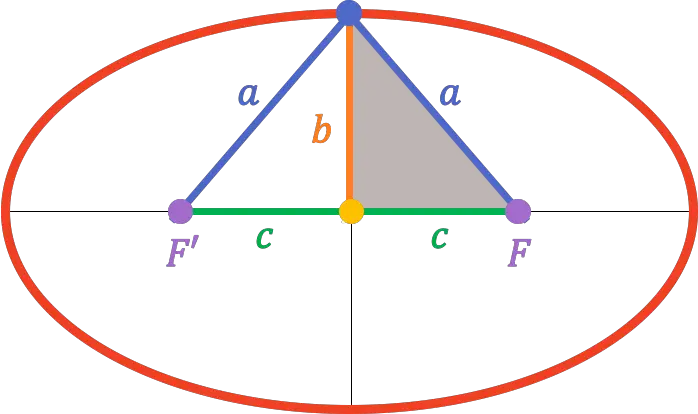
Таким образом, из теоремы Пифагора можно найти связь, существующую между главной полуосью, вторичной полуосью и полуфокусным расстоянием:
![]()
Запомните эту формулу, потому что она будет очень полезна для расчета результатов упражнений с эллипсами.
Эксцентриситет эллипса
Очевидно, что не все эллипсы одинаковы, но некоторые более вытянуты, а другие более приплюснуты. Итак, существует коэффициент, который используется для измерения того, насколько округлен данный эллипс. Этот коэффициент называется эксцентриситетом и рассчитывается по следующей формуле:
![]()
Золото
![]()
— расстояние от центра эллипса до одного из его фокусов и
![]()
длина большой полуоси.
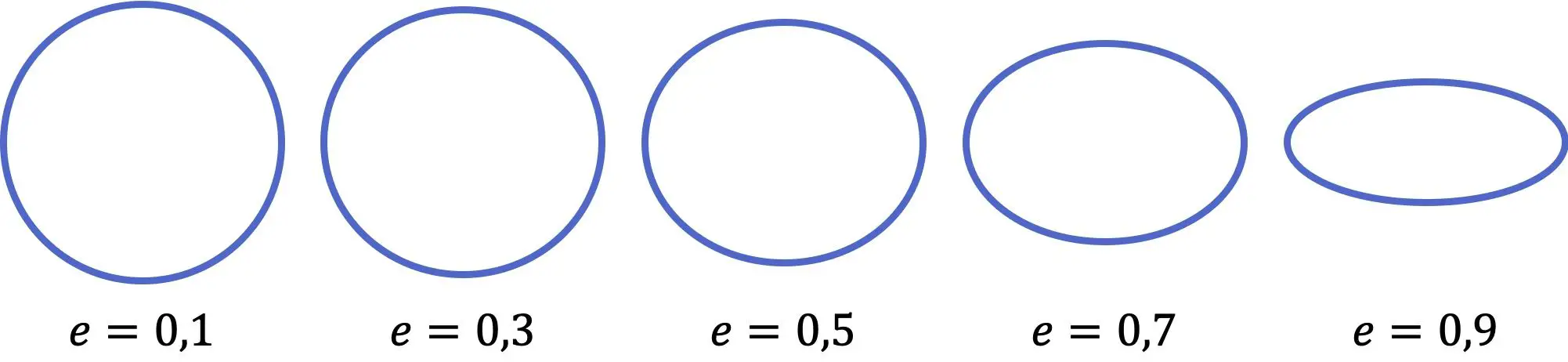
Как видно в предыдущем представлении, чем меньше значение эксцентриситета эллипса, тем больше он напоминает круг, с другой стороны, чем больше коэффициент, тем более сплющенным является эллипс. Кроме того, значение эксцентриситета варьируется от нуля (идеальный круг) до единицы (горизонтальная линия), не включая оба параметра.

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ бм{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1 С(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
Наконец, если эта статья была вам полезна, вас наверняка заинтересуют и наши страницы, посвященные формуле гиперболы и формуле параболы . Вы найдете подробное объяснение того, что такое гипербола и парабола, их уравнения, их характеристики, примеры, решенные упражнения,…