На этой странице вы найдете все об уравнении окружности: обыкновенное уравнение, общее уравнение, другие виды уравнений окружности, когда уравнение окружности верно,… Кроме того, вы увидите примеры того, как найти уравнение окружности. окружности, и вы можете практиковаться с решенными упражнениями.
Обычное уравнение окружности
Прежде чем разобраться, что представляет собой уравнение окружности, давайте вспомним понятие окружности:
Окружность — это геометрическое место точек на плоскости, равноудаленных от фиксированной точки, называемой центром.
Следовательно, все точки окружности находятся на одинаковом расстоянии от ее центра.
Кроме того, круг является одним из четырех конических сечений наряду с эллипсом, параболой и гиперболой. То есть круг можно получить, разрезав конус плоскостью, параллельной его основанию.
Самый простой способ описать окружность в декартовой плоскости — использовать ее обычное уравнение. Итак, формула обычного уравнения окружности имеет следующий вид:
Обычное уравнение окружности :
Золото:
-
это радиус круга.
-
И
координаты центра круга:
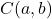
Хотя мы не будем это демонстрировать, поскольку это немного утомительно, это уравнение можно получить из теоремы Пифагора.
Давайте посмотрим, как рассчитывается обыкновенное уравнение окружности на примере:
- Определить обыкновенное уравнение окружности радиуса 5, центром которой является точка
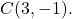
Формула обычного уравнения окружности:
Поэтому нам остается только заменить неизвестное
по значению радиуса и неизвестным
И
координатами X и Y соответственно центра круга:
Итак, обычное уравнение окружности:
Общее уравнение окружности
Другой тип уравнения окружности — это общее уравнение, фактически оно наиболее часто используемое. Затем мы увидим, как получить общее уравнение любой окружности из ее обычного уравнения.
Рассмотрим обычное уравнение окружности:
Если мы разработаем замечательные равенства (или замечательные произведения):
Теперь делаем 3 замены переменных:
И наконец получаем общее уравнение окружности:
Таким образом, формула общего уравнения окружности имеет вид:
где центр круга:
А радиус круга:
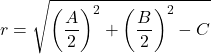
Итак, это уравнение окружности всегда получается из обычного уравнения. Вот пример, чтобы увидеть, как это делается:
- Определить общее уравнение окружности радиуса 6, центром которой является точка
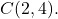
Сначала нам нужно найти обычное уравнение окружности. Для этого воспользуемся его формулой:
И теперь действуем до тех пор, пока не найдем общее уравнение окружности, то есть до тех пор, пока мы не сможем больше упрощать:
Итак, общее уравнение круга:
Хотя задача этого и не требовала, теперь мы можем вычислить центр и радиус найденного уравнения, чтобы убедиться в его правильности.
Для определения центра круга воспользуемся его формулой:
Фактически центр круга совпадает с центром утверждения.
Также проверяем радиус окружности по его формуле:
![\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04dc99d462a8ceb5e6dca936999a4ce8_l3.png "Rendered by QuickLaTeX.com")
И радиус также равен радиусу утверждения. Следовательно, рассчитанное уравнение окружности верно.
Наличие окружности
Все уравнения в виде
соответствуют кругу. Таким образом, чтобы этот тип выражения действительно был уравнением окружности, должны быть выполнены следующие 3 условия:
- Коэффициенты
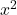
и из
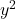
они должны быть равны 1. Имейте в виду, что если обеим переменным предшествовало число, отличное от единицы, но они обе имели один и тот же номер, все уравнение можно было бы разделить на это число так, чтобы их коэффициенты были равны 1.
- В уравнении не может быть члена
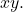
- Следующее выражение должно быть положительным:
Другие типы уравнений окружности
Два уравнения окружности, которые мы видели, обычное уравнение и общее уравнение, наиболее часто используются для математического выражения окружности на плоскости (в R2). Однако существует несколько типов уравнений для описания этого геометрического объекта, ниже приводится объяснение каждого из них.
Каноническое уравнение окружности
Каноническое уравнение или сокращенное уравнение окружности используется для описания любой окружности , центр которой находится в начале координат , то есть в точке (0,0). Указанное уравнение выглядит следующим образом:
Если бы, кроме того, радиус был эквивалентен единице (1), уравнение окружности было бы:
Это последнее уравнение соответствует гониометрической длине окружности, также называемой единичной окружностью или единичным кругом. Это круг радиуса 1 с центром в начале координат.
Уравнения двух концентрических окружностей
Два концентрических уравнения – это те, у которых центр находится в одной точке. И единственное отличие двух концентрических кругов – это радиус.
Таким образом, чтобы это условие выполнялось, уравнения двух концентрических окружностей абсолютно одинаковы, за исключением их независимых членов, которые должны быть разными.
Например, следующие две окружности концентричны, поскольку все их коэффициенты идентичны, за исключением независимых членов:
Параметрическое уравнение окружности
Как и линия, уравнение окружности также можно параметризовать тригонометрическими функциями синуса и косинуса. Таким образом, параметрические уравнения окружности имеют вид:
![\diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)](https://mathority.org/wp-content/ql-cache/quicklatex.com-72dae5b3c5f775661ecb102945bb3fbd_l3.png "Rendered by QuickLaTeX.com")
где точка
является центром круга и
Это ваш отдел.
Решенные задачи уравнения окружности
Упражнение 1
Вычислите общее уравнение окружности радиуса 5, центр которой находится в точке
Чтобы найти общее уравнение окружности, нужно сначала найти ее обыкновенное уравнение. Для этого воспользуемся формулой обычного уравнения окружности:
Зная обычное уравнение, мы работаем, пока не найдем общее уравнение окружности:
Итак, общее уравнение круга:
Упражнение 2
Для каждой из следующих окружностей найдите координаты ее центра и длину ее радиуса.
окружность А)
Длина окружности выражается в виде обыкновенного уравнения, формула которого:
Следовательно, координаты центра круга:
И его радиус:
окружность Б)
Эта окружность выражается в виде общего уравнения, поэтому для расчета координат ее центра необходимо использовать следующую формулу:
С другой стороны, формула для нахождения радиуса круга:
![\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0cdc38937e6c36bb9e6d2ca0814a650_l3.png "Rendered by QuickLaTeX.com")
окружность С)
Длина окружности выражается в виде обыкновенного уравнения, формула которого:
Следовательно, координаты центра круга:
В этом случае уравнение не имеет члена.
ни один
поэтому он центрируется в начале координат:
И его радиус:
Упражнение 3
Какое из следующих уравнений является уравнением окружности?
Чтобы выражение было уравнением окружности, должны выполняться следующие условия:
1. Коэффициенты
и из
Они должны быть равны 1.
2. В уравнении не может быть члена
3.
Поэтому мы должны убедиться, что эти три условия выполняются для каждого уравнения.
Уравнение А)
Коэффициенты
И
равны 1, и уравнение не имеет члена
Поэтому достаточно проверить третье условие:
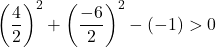
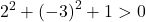
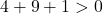
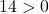Уравнение удовлетворяет трем условиям, поэтому это уравнение окружности.
Уравнение Б)
В уравнении есть член с
с которым уравнение не соответствует окружности.
Уравнение С)
Коэффициенты
И
не равны 1, но мы можем преобразовать уравнение, разделив все члены:
Таким образом, теперь коэффициенты
И
да, они равны 1 и, более того, в уравнении нет члена
Поэтому нам остается лишь подтвердить третье условие:
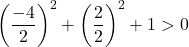
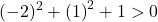
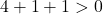
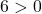Уравнение удовлетворяет трем условиям, поэтому это уравнение окружности.
Уравнение Д)
Коэффициенты
И
равны 1, и уравнение не имеет члена
Поэтому достаточно проверить третье условие:
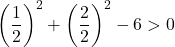
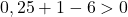
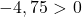Уравнение не удовлетворяет последнему условию, поэтому оно не является уравнением окружности .
Упражнение 4
Определите уравнение окружности, проходящей через следующие три точки:
Общее уравнение любой окружности:
Поэтому нам необходимо подставить координаты точек в уравнение окружности, чтобы найти параметры
И
По первой точке находим коэффициент
По второй точке находим коэффициент
![\begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-12719654d98ba81f0a7d45e587478e6d_l3.png "Rendered by QuickLaTeX.com")
А из третьего пункта находим коэффициент
![\begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1e69c28996a8fbfa14189c48a295095_l3.png "Rendered by QuickLaTeX.com")
В заключение общее уравнение длины окружности выглядит следующим образом:
Упражнение 5
Если противоположными концами круга являются следующие две точки:
Что представляет собой обычное уравнение окружности?
Если две точки являются крайними точками круга, его центром будет середина между этими двумя точками:
С другой стороны, диаметр круга будет расстоянием между двумя точками, которое можно рассчитать, используя величину вектора, который образуют две точки:
А радиус круга равен половине диаметра:
Таким образом, обычное уравнение окружности имеет вид:
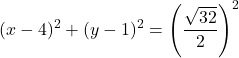
Наконец, если эта статья была вам полезна, вас наверняка заинтересуют наши страницы с гиперболой (математика) и параболой (математика) . Вы найдете подробное объяснение того, что такое гипербола и парабола, их уравнения, их характеристики, примеры, решенные упражнения…