Здесь вы найдете формулу, используемую для расчета расстояния между точкой и линией. Кроме того, вы сможете увидеть несколько примеров и решенных упражнений на расстояние между точками и прямыми и даже приложения, которые имеет эта операция (например, нахождение расстояния между параллельными прямыми).
Формула расстояния между точкой и прямой
Расстояние между точкой и линией — это кратчайшее расстояние между этой точкой и линией. Математически это минимальное расстояние эквивалентно длине отрезка, проведенного от точки до линии и перпендикулярного этой линии.
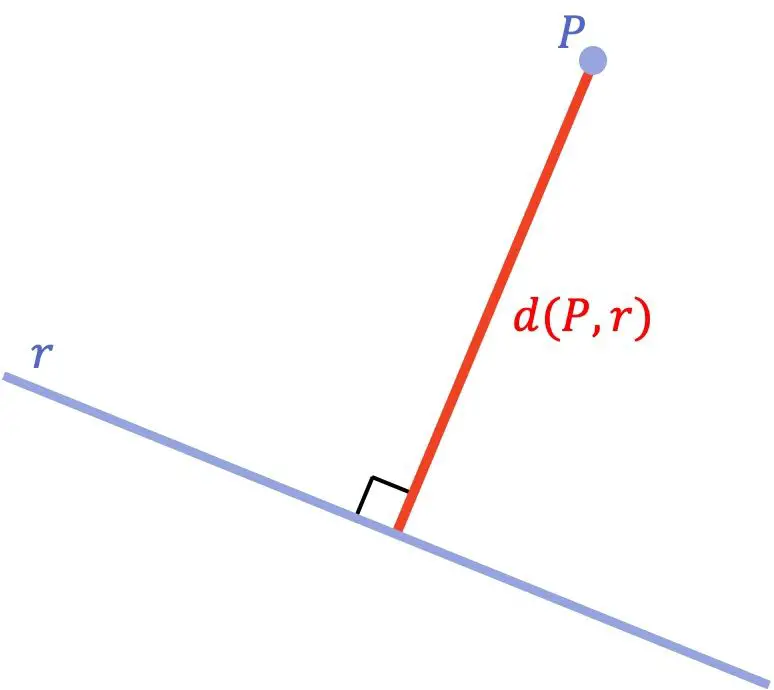
Разобравшись с геометрической концепцией расстояния между точкой и линией, давайте посмотрим, какая формула используется для расчета указанного расстояния:
Учитывая неявное (или общее) уравнение прямой и координаты любой точки на плоскости:
![]()
Формула расстояния между точкой и линией :
![]()
Важно: Обратите внимание, что уравнение линии в формуле имеет форму неявного (или общего) уравнения, поэтому, если у нас есть линия, выраженная в уравнении другого типа, нам нужно сначала передать ее неявному уравнению, а затем мы можем применить формулу.
Пример расчета расстояния между точкой и линией
Ниже вы можете увидеть пример расчета расстояния между точкой и линией:
- Найдите расстояние между точками

и закон

![]()
Чтобы рассчитать расстояние между точкой и линией, просто примените ее формулу:
![]()
Теперь мы заменим каждый термин его значением:
![]()
И наконец вычисляем расстояние:
![]()
Расстояние между двумя параллельными линиями
Одним из применений вычисления расстояния между линией и точкой является поиск расстояния между параллельными линиями.
Очевидно, что чтобы понять концепцию, которую мы объясним ниже, вы должны знать , что такое параллельные линии , поэтому, если вы не знаете точно их определения, мы оставляем вам ссылку, где мы подробно объясняем это, и вы также сможете увидеть примеры. параллельных линий.
Чтобы найти расстояние между двумя параллельными линиями, просто возьмите точку на одной из двух линий и вычислите расстояние от этой точки до другой линии.

Итак, для определения расстояния между двумя параллельными прямыми также используется формула расстояния между прямой и точкой.
С другой стороны, если при использовании формулы мы получим расстояние 0 единиц, это означает, что линии в какой-то точке касаются друг друга и, следовательно, линии не параллельны, а пересекаются, совпадают или перпендикулярны. При желании вы можете проверить отличия этого типа линий на нашем сайте.
Итак, давайте посмотрим, как решить проблему расстояния между двумя параллельными линиями на примере:
- Найдите расстояние между следующими двумя параллельными прямыми:
![]()
Первое, что нам нужно сделать, это поставить точку на одной из линий (той, которая вам нужна). В данном случае мы рассчитаем точку на линии
![]()
Для этого необходимо присвоить значение одной из переменных, например мы сделаем
![]()
![]()
И теперь мы очищаем другую переменную (
![]()
) полученного уравнения, чтобы узнать, сколько оно стоит в данный момент:
![]()
![]()
![]()
Следовательно, точка, полученная из прямой
![]()
Восток:
![]()
И как только у нас уже есть точка на линии, мы вычисляем расстояние от этой точки до другой линии по формуле:
![]()
![]()
Решены задачи о расстоянии между точкой и линией.
Упражнение 1
Рассчитать расстояние между точками
![]()
и закон
![]()
![]()
Чтобы найти расстояние между точкой и линией, просто примените ее формулу:
![]()
Заменяем каждый член его значением и вычисляем расстояние:
![]()
Упражнение 2
Каково расстояние между точкой
![]()
и закон
![]()
?
![]()
В этом случае уравнение линии имеет неявный (или общий) вид. Вместо этого, чтобы использовать формулу расстояния от точки до линии, линия должна быть выражена в виде неявного уравнения. Поэтому мы должны сначала преобразовать линию и передать ее неявному уравнению (просто передать все члены с одной стороны уравнения):
![]()
И как только линия уже имеет явный вид, мы можем теперь использовать формулу для расстояния между точкой и линией:
![]()
Поэтому мы заменяем каждый член его значением и вычисляем расстояние:
![]()
Упражнение 3
Каково расстояние между следующими двумя линиями?
![]()
Сначала проверим, что это две параллельные прямые. Для этого коэффициенты при переменных
![]()
И
![]()
должны быть пропорциональны друг другу, но не независимым членам:
![]()
Действительно, линии параллельны, поэтому мы можем применить эту процедуру.
Теперь нам нужно получить точку от одной из линий (той, которую вы хотите). В данном случае мы рассчитаем точку на линии
![]()
Для этого необходимо присвоить значение одной из переменных, например мы сделаем
![]()
![]()
И теперь мы очищаем другую переменную (
![]()
) полученного уравнения, чтобы узнать его значение в этой точке:
![]()
![]()
![]()
Так что точка, полученная из прямой
![]()
Восток:
![]()
Как только мы узнаем точку на линии, мы вычисляем расстояние от этой точки до другой линии по формуле:
![]()
![]()
Упражнение 4
Вычислить значение неизвестного
![]()
так что расстояние между точками
![]()
и закон
![]()
то есть 5 единиц.
![]()
Сначала мы должны применить формулу расстояния между точкой и линией:
![]()
Теперь заменим каждое слагаемое его значением и упростим выражение:
![]()
В постановке задачи нам сказано, что расстояние между точкой и прямой должно быть равно 5, поэтому приравниваем предыдущее выражение к 5:
![]()
И решаем полученное уравнение. В числителе дроби стоит абсолютная величина, поэтому надо разбирать отдельно, когда абсолютная величина положительная, а когда отрицательная:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, существуют два возможных значения
![]()
правильный:
![]()
или
![]()