На этой странице вы найдете все о явном уравнении прямой: что это такое, какова его формула, примеры расчета и т.д. Вы также найдете подробное объяснение того, что означает наклон, и точку пересечения явного уравнения. Более того, вы увидите разные примеры и сможете практиковаться, выполняя упражнения, решая шаг за шагом.
Каково явное уравнение линии?
Помните, что математическое определение линии — это набор последовательных точек, которые представлены в одном направлении без кривых или углов.
Итак, явное уравнение линии — это способ выразить любую линию математически. Для этого вам просто нужно знать наклон линии и точку ее пересечения с осью Y.
Формула явного уравнения линии
Формула явного уравнения линии :
![]()
Золото
![]()
это наклон линии и
![]()
его точка пересечения по оси Y, то есть высота, на которой он пересекает ось Y.
Давайте посмотрим , как рассчитывается явное уравнение линии на примере:
- Напишите явное уравнение прямой, проходящей через точку
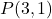
и уклон m=2.
Формула явного уравнения линии:
![]()
В этом случае утверждение сообщает нам, что наклон линии равен m=2, поэтому уравнение линии будет следующим:
![]()
Поэтому достаточно вычислить коэффициент n. Для этого нам необходимо подставить в ее уравнение точку, принадлежащую прямой. И в этом случае утверждение говорит нам, что линия проходит через точку
![]()
Еще:
![]()
![]()
И решаем полученное уравнение, чтобы найти значение n:
![]()
![]()
![]()
![]()
Таким образом, явное уравнение линии имеет вид:
![]()
Имейте в виду, что помимо явного уравнения существуют и другие способы аналитического выражения линии. Например, векторное уравнение , которое представляет собой тип линейного уравнения, отличающийся от всех остальных, поскольку вектор направления и точка на линии выражаются своими собственными координатами. По ссылке вы можете увидеть, что это такое и почему оно такое особенное.
Значение параметров m и n
Как мы видели при определении явного уравнения линии, параметр
![]()
это наклон линии и
![]()
это y-перехват. Но что это значит? Давайте посмотрим на это на графическом представлении линии:

Термин «независимый»
![]()
— точка пересечения линии с осью компьютера (ось OY). На графике выше
![]()
равно 1, поскольку линия пересекает ось y в точке y=1.
С другой стороны, термин
![]()
указывает наклон линии , то есть ее наклон. Как вы видите на графике,
![]()
равно 2, так как линия поднимается на 2 единицы по вертикали за 1 единицу по горизонтали.
Очевидно, что если наклон положителен, функция возрастает (уходит вверх), а если наклон отрицательный, функция убывает (уменьшается).
Вычислить наклон линии
Кроме того, существует три различных способа численного определения наклона линии:
- Даны две разные точки на прямой

И

Наклон линии равен:
- Ага

– вектор направления линии, ее наклон:
- Ага

— угол, образованный линией с осью абсцисс (ось X), наклон линии эквивалентен тангенсу указанного угла:
![]()
![]()
![]()

Относительное положение линий
Наконец, наклон линии также используется для определения взаимосвязи между несколькими линиями. Поскольку две параллельные линии имеют одинаковый наклон и, с другой стороны, если наклон одной линии является отрицательной величиной, обратной наклону другой линии, это означает, что эти две линии перпендикулярны .


Вычислить явное уравнение прямой, проходящей через две точки
Очень типичная задача — найти явное уравнение прямой по двум точкам, через которые она проходит. Давайте посмотрим, как она решается на примере:
- Определите явное уравнение прямой, проходящей через следующие две точки:
![]()
Чтобы найти явное уравнение линии, нужно знать, чего стоят параметры m и n. Поэтому сначала мы вычисляем наклон линии, используя формулу двоеточия:
![]()
![]()
И тогда мы можем найти точку пересечения оси Y, подставив точку на прямой в уравнение:
![]()
![]()
![]()
![]()
![]()
Итак, явное уравнение линии:
![]()
Нахождение явного уравнения по неявному уравнению
Наконец, еще один тип задач, с которым мы часто сталкиваемся, — это нахождение явного уравнения прямой из ее неявного уравнения (также называемого общим или декартовым уравнением). Очевидно, чтобы понять следующий метод, вам нужно точно знать, что представляет собой подразумеваемое уравнение и как оно работает; но если вы его совсем не помните, вы можете посмотреть по ссылке.
Итак, если вы уже освоили неявное (или общее) уравнение прямой, давайте посмотрим, как работает эта процедура:
- Найдите явное уравнение следующей строки:
![]()
Все, что нам нужно сделать, чтобы найти явное уравнение прямой, — это найти переменную
![]()
Поэтому мы принимаем условия без
![]()
с другой стороны уравнения:
![]()
Теперь очищаем переменную
![]()
![]()
И наконец, упрощаем:
![]()
![]()
![]()
Следовательно, наклон этой линии равен
![]()
и его точка пересечения с Y равна 4.
Решенные задачи с явными уравнениями
Упражнение 1
Определите наклон и точку пересечения оси Y следующих линий:
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 3x-1 & \qquad & B) \ y=5x+2 \\[2ex] C) \ y=-x+3 & \qquad & D) \ 4x+2y-6=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3077643710747855c7b59a93551fbad8_l3.png)
Явное уравнение линии следует следующей формуле:
![]()
Золото
![]()
это наклон и
![]()
компьютер в начале координат. Еще:
![Rendered by QuickLaTeX.com \bm{A)} \ y= 3x-1 \ \begin{cases} m = 3 \\[2ex] n=-1\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f62bc45bc23ea6c323b1a5d95ba40ca2_l3.png)
![Rendered by QuickLaTeX.com \bm{B)} \ y= 5x+2 \ \begin{cases} m = 5 \\[2ex] n=2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-683f74baf43275be7565fc744704e6ed_l3.png)
![Rendered by QuickLaTeX.com \bm{C)} \ y= -x+3 \ \begin{cases} m = -1 \\[2ex] n=3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39e8a1c6dbe8e5ff8db1fc8b08c4c95d_l3.png)
Последняя строка выражается неявным уравнением, поэтому сначала нам нужно передать ее явному уравнению (решить
![]()
), то мы можем определить параметры:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{cases} m = -2 \\[2ex] n=3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50c2bb75ae362e0a2dee3a3670459df3_l3.png)
Упражнение 2
Найдите явное уравнение прямой, проходящей через точку
![]()
и имеет наклон
![]()
Формула явного уравнения линии:
![]()
В этом случае наклон линии должен быть равен -2, поэтому уравнение линии будет иметь следующий вид:
![]()
Поэтому достаточно вычислить коэффициент n. Для этого необходимо подставить в ее уравнение точку, принадлежащую прямой, и решить полученное уравнение:
![]()
![]()
![]()
![]()
![]()
Короче говоря, явное уравнение линии таково:
![]()
Упражнение 3
Найдите явное уравнение прямой, проходящей через следующие две точки:
![]()
Чтобы найти явное уравнение линии, нужно знать, чего стоят параметры m и n. Поэтому мы сначала вычисляем наклон линии по координатам двух точек:
![]()
![]()
А затем определяем точку пересечения, подставив точку на прямой в уравнение:
![]()
![]()
![]()
![]()
Итак, явное уравнение линии:
![]()
Упражнение 4
Вычислите явное уравнение линии, образующей угол 45° с осью X и проходящей через начало координат.
Если линия составляет угол 45 градусов с осью OX, ее наклон составит:
![]()
![]()
И как только мы узнаем наклон линии, мы можем вычислить точку пересечения оси y, подставив точку на линии в уравнение. Кроме того, оператор сообщает нам, что линия проходит через начало координат, а это значит, что она проходит через точку (0,0). Еще:
![]()
![]()
![]()
Итак, явное уравнение линии:
![]()
Упражнение 5
Найдите явное уравнение прямой, параллельной прямой
![]()
и что происходит через точку
![]()
быть прямым
![]()
![]()
Чтобы линия была параллельна линии
![]()
оба должны иметь одинаковый наклон, поэтому:
![]()
![]()
И как только мы узнаем наклон линии, мы можем вычислить точку пересечения оси y, подставив точку, принадлежащую линии, в уравнение:
![]()
![]()
![]()
![]()
![]()
Итак, явное уравнение линии:
![]()
Упражнение 6
Каково явное уравнение каждой изображенной на графике линии?

синий правый
Синяя линия увеличивается на один Y для каждого
![]()
прямо зеленый
Зеленая линия увеличивается на 3 Y для каждого X, поэтому ее наклон равен 3. Кроме того, линия пересекает ось Y в точке -4, поэтому ее точка пересечения с Y равна -4.
![]()
Красная линия
Красная линия уменьшается на два Y для каждого X, поэтому ее наклон равен -2. А линия пересекает ось Y в точке y=-2, поэтому ее точка пересечения с Y также равна -2.
![]()