Метод наименьших квадратов — математический инструмент для поиска наилучшей прямой, соответствующей набору точек . Мы объясняем вам это просто:
Представьте, что у вас есть несколько точек на графике, разбросанных тут и там. Вы хотите найти прямую линию, которая лучше всего «соответствует» этим точкам, чтобы минимизировать расстояние между линией и точками . В этом и заключается идея метода наименьших квадратов.
В методе используется формула для расчета уравнения линии, которая минимизирует сумму квадратов разностей между точками и линией. То есть ищет линию, имеющую наименьшее «отклонение» от точек.
Говоря простым языком, метод наименьших квадратов полезен для анализа данных, полученных в ходе расследования, с целью линейного выражения их поведения, уменьшения ошибок украденной информации.
Кто создал метод наименьших квадратов?
Метод наименьших квадратов, фундаментальный инструмент в статистике и анализе данных, приписывается немецкому математику Карлу Фридриху Гауссу , который предложил его в 1794 году. Однако Гаусс опубликовал его только в 1809 году .
Интересно, что подобную версию в 1805 году опубликовал французский математик Андриен-Мари Лежандр , разработав ее самостоятельно.
Оба математика помогли создать этот метод, который широко используется в различных дисциплинах для согласования моделей с наблюдаемыми данными и получения точных прогнозов.
Формула наименьших квадратов
Безусловно, чтобы понять, что включает в себя этот метод, необходимо объяснить его формулу и процесс его реализации. Вот подробное объяснение формулы наименьших квадратов:
определить проблему
Допустим, у вас есть набор данных с двумя переменными: независимой переменной (x) и зависимой переменной (y), и вы хотите подогнать к этим данным прямую линию.
Цель состоит в том, чтобы найти значения коэффициентов уравнения линии (точки пересечения и наклона), которое минимизирует сумму квадратов разностей между реальными значениями y и значениями, предсказанными уравнением. приталенная линия.
Вычислить уравнение линии
Уравнение прямой имеет вид y = mx + b, где m — наклон, а b — точка пересечения оси y. Формула наименьших квадратов для расчета значений myb:
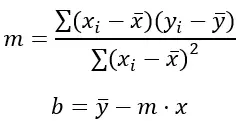
Золото:
Σ представляет собой сумму значений.
x i и y i — значения переменных x и y соответственно для каждой точки данных.
x̄ и ş — средние значения x и y соответственно.
(x i – x̄) и (y i – ş) — это разности между значениями x и y и их соответствующими средними значениями.
(x i – x̄) 2 — это квадрат разницы между значением x и его средним значением.
интерпретировать результаты
После того, как вы вычислили значения m и b по формуле, вы можете использовать их для получения уравнения подобранной линии. Например, если у вас m = 2 и b = 3, то уравнение подобранной линии будет иметь вид y = 2x + 3. Это позволяет вам делать прогнозы или оценки значений y для разных значений x. на основе скорректированного права.
Когда применяется метод наименьших квадратов?
Вы, наверное, спросите себя, когда используется этот метод? Это очень полезно в различных ситуациях! Например, если вы хотите проанализировать экспериментальные или исследовательские данные, чтобы найти взаимосвязь или тенденцию .
Предположим, вы исследуете связь между ценой дома и его размером в квадратных метрах. Вы можете использовать метод наименьших квадратов, чтобы найти прямую линию, которая лучше всего соответствует данным и дает четкое представление об этой взаимосвязи.
Он также используется в экономике для моделирования и прогнозирования таких переменных, как спрос на продукцию или поведение цен . Кроме того, в технике метод наименьших квадратов применяется для адаптации математических моделей к данным тестирования или моделирования.
Метод наименьших квадратов — мощный и универсальный инструмент, который используется во многих областях обучения и работы для анализа данных и поиска важных взаимосвязей.
Приложения метода наименьших квадратов в других теоремах
Помимо использования самого по себе, метод наименьших квадратов очень полезен в других теоремах. Давайте посмотрим немного больше на эту тему ниже.
Теорема о регрессии
Он широко используется в теореме регрессии для поиска наилучшей линии, соответствующей набору данных . Например, вы можете использовать его для анализа взаимосвязи между высотой растения и количеством получаемого им света, чтобы определить, как растение будет расти в различных условиях освещения.
Интерполяция теоремы
В этом случае метод наименьших квадратов также применяется в теореме интерполяции, чтобы найти полиномиальную функцию , которая лучше всего соответствует набору точек. Например, вы можете использовать его для аппроксимации траектории движущегося объекта на основе данных о положении и времени.
Теорема аппроксимации кривой
Он используется в теореме подбора кривой, чтобы найти кривую, соответствующую набору данных . Это полезно в таких приложениях, как моделирование климатических данных для прогнозирования изменения климата или прогнозирования траектории снаряда.
Теорема анализа Фурье
В теореме анализа Фурье метод наименьших квадратов используется для аппроксимации периодической функции на основе ряда дискретных данных . Это относится к передаче данных и сжатию изображений и звука.
Теорема нелинейной регрессии
Наконец, метод наименьших квадратов также применяется в теореме нелинейной регрессии, чтобы найти лучшую кривую, которая соответствует набору данных , который не подчиняется линейной зависимости . Например, вы можете использовать его для анализа того, как концентрация химического вещества влияет на скорость реакции.
Пример метода наименьших квадратов
Чтобы лучше понять, как можно применить метод наименьших квадратов, давайте рассмотрим пример ниже.
Предположим, у вас есть следующие данные о высоте (в сантиметрах) растения в разные недели:
| Неделя | рост в сантиметрах |
| 1 | десять |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | двадцать |
Вы хотите найти лучшую прямую линию, соответствующую этим данным, чтобы спрогнозировать будущую высоту растения.
Шаг 1 : Постройте график данных
Первое, что нужно сделать, это нанести данные на диаграмму рассеяния. По оси X будут отображаться недели, а по оси Y — рост в сантиметрах. Вот график:
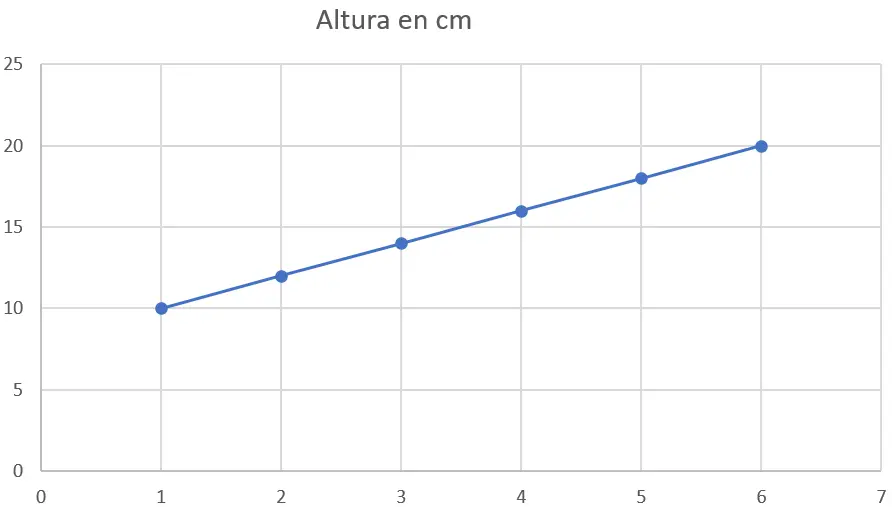
Шаг 2. Примените метод наименьших квадратов.
Метод наименьших квадратов стремится найти линию, которая минимизирует сумму квадратов разностей между фактическими данными и значениями, предсказанными линией. В этом случае линия представляется уравнением линии: y = mx + b, где «y» — высота, «x» — недели, «m» — наклон линии, а «b» — перехват по оси Y.
Для нахождения значений «m» и «b», минимизирующих сумму квадратов разностей, используются следующие формулы:
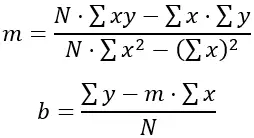
Где N — количество точек данных (в данном случае 6), Σxy — сумма недель, умноженная на высоту, Σx — сумма недель, Σy — сумма высот, а Σx 2 — сумма квадратов недель. .
Применяя эти формулы к данным о высоте, получаем:
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
Подставив эти значения в формулы для «m» и «b»:
м = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 2 ) ≈ 2,07
б = (90 – 2,07 · 21) ÷ 6 ≈ 3,24
Следовательно, уравнение прямой, соответствующей данным о высоте, имеет вид: y.