Комплексные числа — это набор, состоящий из действительных и мнимых чисел . Эти два последних числовых набора можно представить графически, используя действительную и воображаемую линию. А когда мы помещаем обе линии в одну плоскость, образуется всем известная комплексная плоскость.
Что такое комплексный план?
Комплексная плоскость образована действительной осью (ось X), которая эквивалентна действительной линии, и, с другой стороны, воображаемой осью (ось Y), которая концептуализирует воображаемую линию.
Следует отметить, что в этот план включены все комплексные числа. Поэтому, каким бы маленьким или малым оно ни было и в какой форме не было записано комплексное число, его можно изобразить на плане графически. Итак, давайте посмотрим, как эти числа представляются в комплексной плоскости.
Как построить график комплексных чисел на комплексной плоскости?
Как мы уже знаем (а если не знаете, советуем прочитать нашу статью о комплексных числах ), существует три способа записи комплекса: биномиальная форма, полярная форма и тригонометрическая форма. Каждый из них выражает комплексное значение в соответствии с разной структурой, поэтому метод создания графических представлений различен.
Далее мы объясним процедуру, которой следует следовать в трех случаях:
Представление в биномиальной форме
Когда у нас есть комплексное число в биномиальной записи , что является наиболее распространенным, мы должны посмотреть на структуру числа:

где а — действительная часть, а б — мнимая часть.
Зная это, мы делаем вывод, что значение a — это то, которое мы используем для абсцисс (реальная ось), а значение b — это то, которое мы используем для компьютера (мнимая ось). На следующем примере вы поймете это лучше.
Попробуем представить число: 3+2i.
Первым делом нужно нарисовать график (обратив внимание, что горизонтальная ось — реальная, а вертикальная — воображаемая):

Затем мы находим точку графика в декартовых координатах (x, y), которые выводим из комплексного числа. В этом практическом примере наша точка — (3, 2).
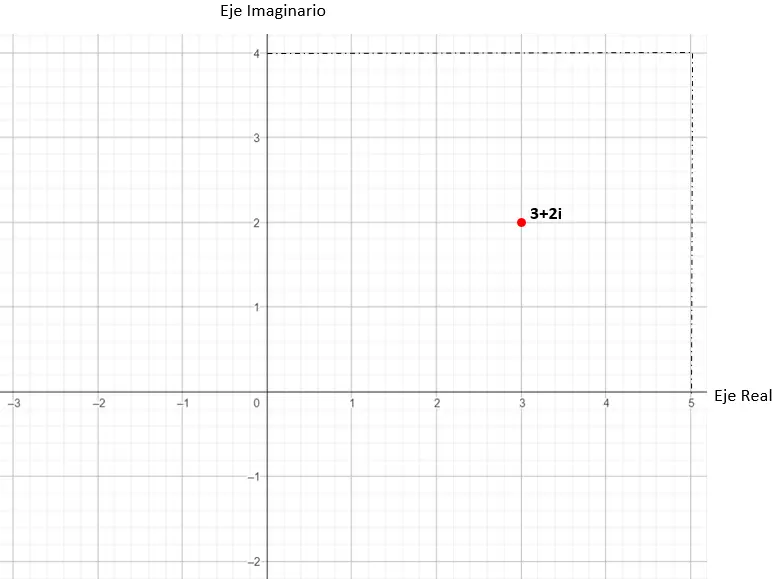
Таким образом, значение 3 + 2i будет представлено в комплексной плоскости.
Представление в полярной форме
Теперь мы увидим, как комплексное число представляется в полярной форме . Чтобы полностью понять этот метод, вам необходимо знать, что полярная запись определяет комплексное число на основе модуля и аргумента. Которые используются в графическом представлении как полярные координаты (а не как декартовы координаты!).
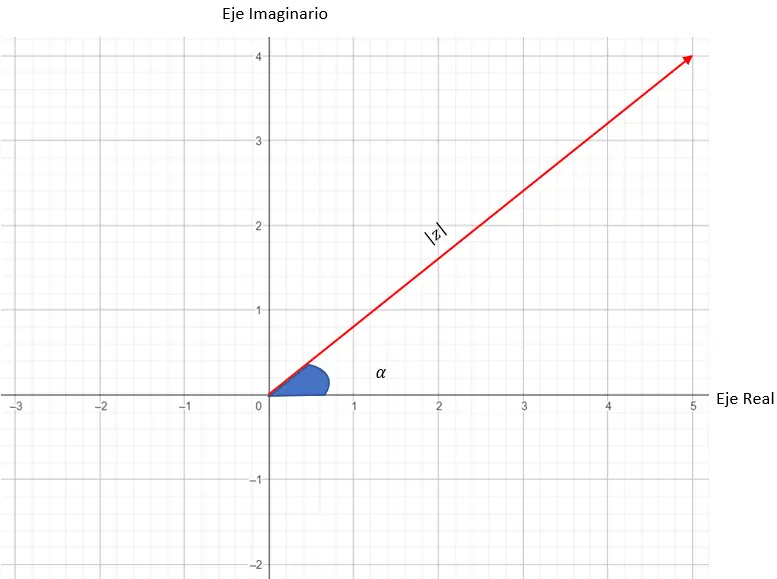
А главная особенность полярной системы координат заключается в том, что положение точки описывается посредством вектора и угла (в отличие от предыдущего метода). Что соответствует модулю и аргументу комплексных чисел. Далее мы покажем вам универсальную формулу полярной формы комплексного числа:

Где |z| – модуль, а α – аргумент. Эти две переменные преобразуются в плане следующим образом:
- Модуль: это длина, которая определяет вектор (между началом координат и точкой, эквивалентной нашему числу).
- Аргумент: угол, который вектор образует с осью X.
Следовательно, модуль комплексного числа соответствует длине вектора, который мы используем для построения графика. А аргументом или углом комплексного числа является угол между вектором и осью X. Ниже вы можете увидеть диаграмму, на которой размещены все переменные :
Теперь попробуем представить число: 3 45 .
Сначала нам нужно идентифицировать модуль и аргумент:
- Модуль: 3.
- Аргумент: 45 градусов.
Далее нам нужно найти на графике точки, имеющие модуль, равный 3, в этом случае подойдет любая точка на окружности радиуса 3.
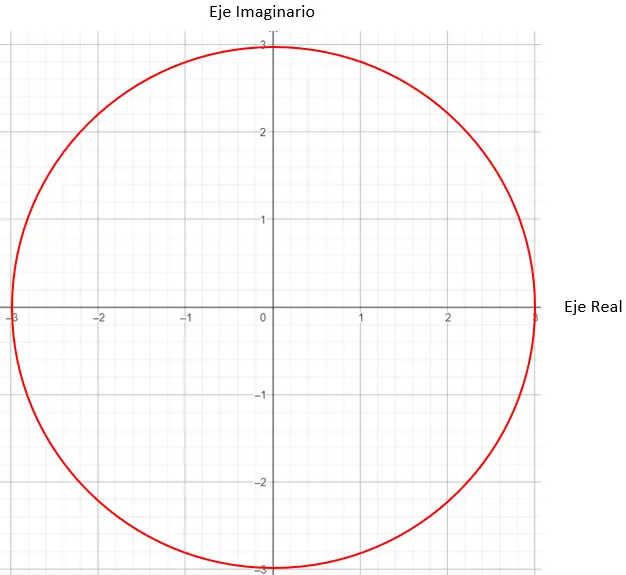
И чтобы окончательно определить, что это за точка, мы должны поставить условие, что вектор, генерируемый модулем, и начало координат должны составлять угол 45 градусов с осью X.
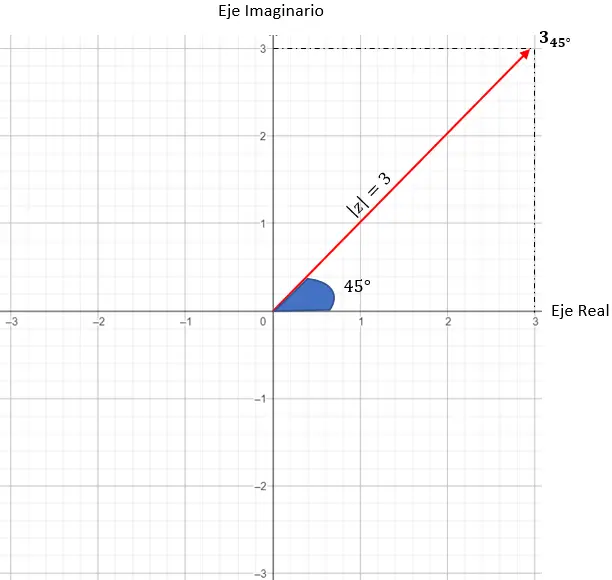
И у нас уже есть комплексное число, представленное в полярной записи.
Представление в тригонометрической форме
Наконец, нам еще предстоит объяснить, как комплексное число представляется в тригонометрической форме . Этот случай и предыдущий практически одинаковы, поскольку полярная форма и тригонометрическая форма используют одни и те же данные для выражения комплексного числа: модуль и аргумент. Это меняет только структуру выражения:

Где, |z| – модуль, а α – аргумент.
Поэтому мы должны воспользоваться тем же методом, что и в предыдущем случае: использовать модуль как «длину», а аргумент как угол. Увидев следующий пример, вы поймете это лучше.
Представим z = 4 · (cos (45) + i · sin(45)).
Первым делом необходимо определить модуль и угол:
- Модуль: 4.
- Аргумент: 45 градусов.
Далее нам нужно найти на графике точки, имеющие модуль, равный 4, в этом случае подойдет любая точка на окружности радиуса 4.
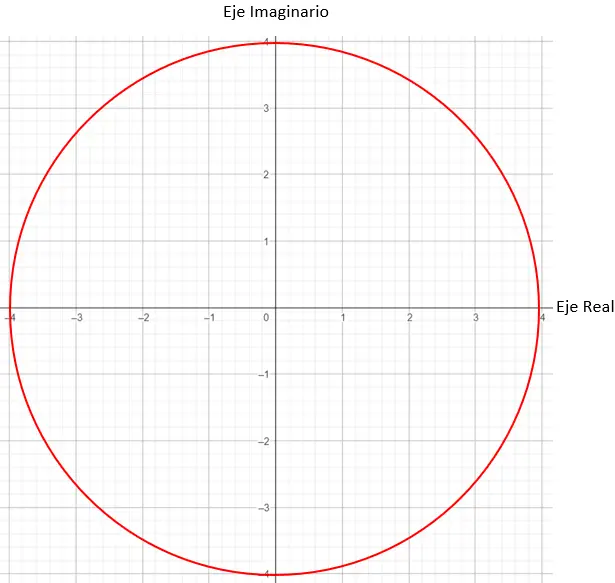
И, наконец, мы находим точную точку, требуя, чтобы угол, образованный между вектором модуля и осью X, составлял 45 градусов, как нам говорит аргумент.
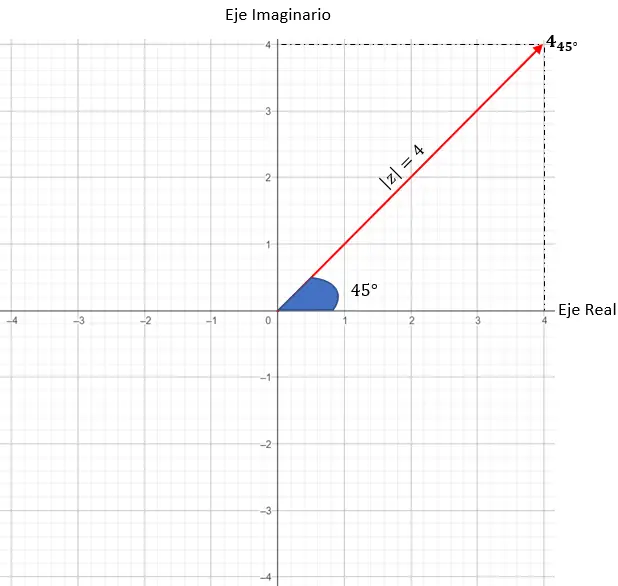
И так мы представляем комплексное число в тригонометрической форме.
Комплексное упражнение «Самолет».
В завершение этой публикации мы собираемся предложить последнее упражнение. Мы настоятельно рекомендуем вам решить ее, потому что таким образом вы закрепите знания, изложенные в этой статье.
Доказательство графического изображения следующих трех комплексных чисел на комплексной плоскости:
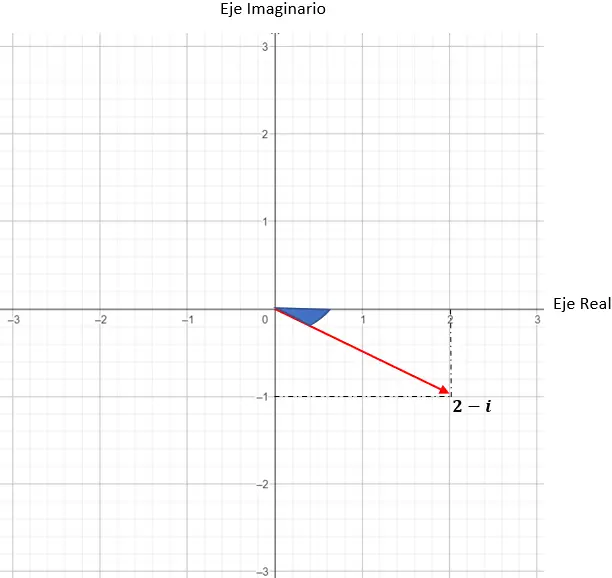
г = 2 – я
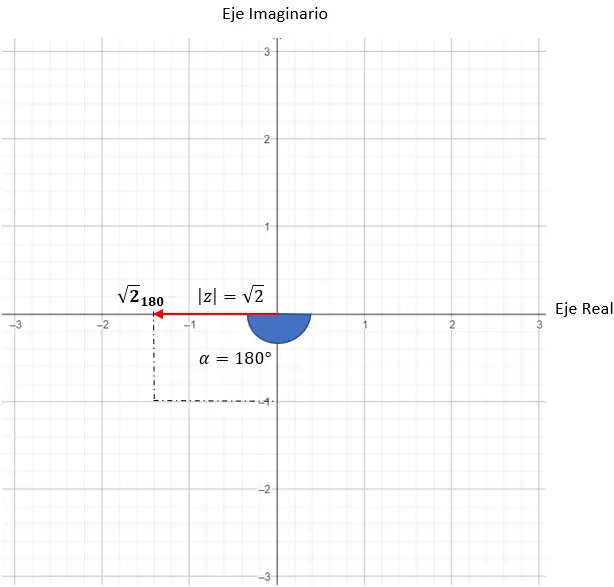
ш = √2180
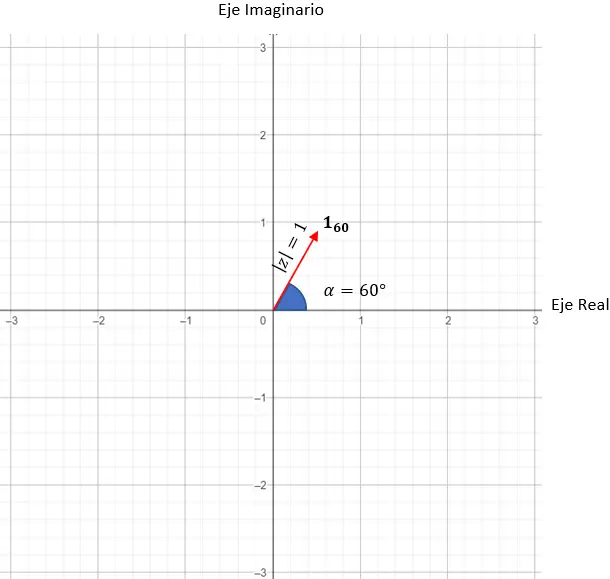
р = соз(60) + я грех(60)
Узнайте больше о сложном плане
- Комплексные числа
- мнимые числа