Формула Эйлера — математическое понятие, связывающее два элементарных понятия математики: комплексные числа и тригонометрию. Это делает ее одной из наиболее важных концепций и имеющей наибольшее количество приложений во всей математике. В этой статье мы увидим, как выглядит эта формула и все ее применения.
Что такое формула Эйлера?
Формула Эйлера — это фундаментальное математическое уравнение, основанное на числе Эйлера , которое связывает комплексные числа с тригонометрией. Он был открыт швейцарским математиком Леонардом Эйлером в 18 веке и с тех пор используется в самых разных областях, от физики до информатики.
Формула Эйлера записывается как e ix = cos(x) + i sin(x) , где e — основание натурального логарифма, i — мнимая единица (определяемая как квадратный корень из -1), а x — действительное число. число. Это уравнение указывает, что комплексное число e ix равно сумме действительного числа cos(x) и произведения мнимого числа i на действительное число sin(x).

Важность формулы Эйлера заключается в том, что она позволяет выражать комплексные числа через действительные числа и тригонометрию, что упрощает манипулирование ими и их вычисление.
Доказательство формулы Эйлера
Доказательство формулы Эйлера основано на использовании ряда Тейлора для показательной функции и тригонометрического тождества для косинуса и синуса.
Сначала рассмотрим ряд Тейлора для показательной функции:

Затем мы заменяем x на ix в приведенном выше уравнении, где i — мнимая единица измерения (квадратный корень из -1):
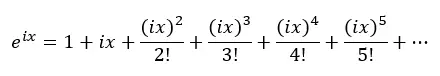
Итак, применим степени i и подставим в предыдущее уравнение:
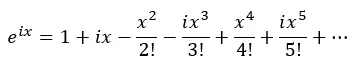
Теперь сгруппируем действительные члены и члены с i:
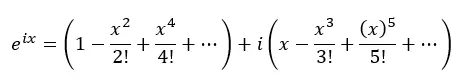
Фактически, каждая из приведенных выше круглых скобок представляет собой ряд Тейлора для косинуса и синуса:
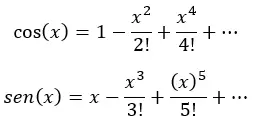
Наконец, упрощаем (заменяя каждое выражение в скобках косинусом и синусом x) и получаем:

Пример формулы Эйлера
Теперь, когда вы знаете, как работает эта математическая формула, рекомендуем попробовать решить следующий практический пример: Выразите комплексное число e 2i (в радианах) в биномиальной форме:
Основное применение формулы Эйлера — преобразование комплексного числа, выраженного в экспоненциальной форме, в биномиальную форму. Поэтому мы будем использовать формулу : e ix = cos(x) + i sin(x)
е 2i = cos(2) + я sin(2)
е2i = -0,416 + 0,909i
И у нас уже было бы число в биномиальной форме. Отсюда мы можем сделать графическое представление в комплексной плоскости . Для этого необходимо понимать, что комплексное число изображается на комплексной плоскости, используя в качестве координат действительную часть по абсциссе (ось X) и мнимую часть по ординате (ось Y).
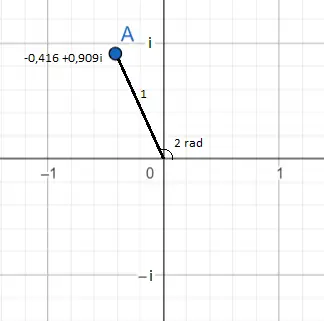
На предыдущем изображении показано комплексное число e 2i , равное -0,416 + 0,909i. Это можно увидеть как точку синего цвета. Его расположение на плоскости можно увидеть с двух ракурсов .
Первый и наиболее очевидный — с представлением числа в биномиальной форме : -0,416 (по оси абсцисс) и 0,909 (по компьютеру). А второй — в экспоненциальной форме : модуль e 2i равен 1, потому что это число, стоящее перед e (поскольку перед e нет числа, мы должны представить, что перед e стоит 1) а в показателе степени стоит 2, следовательно, аргумент или угол эквивалентен двум радианам.
Если вы не совсем поняли этот последний абзац , рекомендуем вам прочитать нашу статью о комплексных числах. Что ж, здесь мы очень подробно объясняем различные способы записи комплексного числа и всех его свойств.
Графическое представление формулы Эйлера
В предыдущем примере вы могли увидеть, как применяется формула Эйлера и как она представлена графически на комплексной плоскости. Но если мы пойдем немного дальше и попытаемся представить функцию, эквивалентную формуле Эйлера, мы обнаружим нечто очень любопытное: она генерирует круг радиуса 1 :
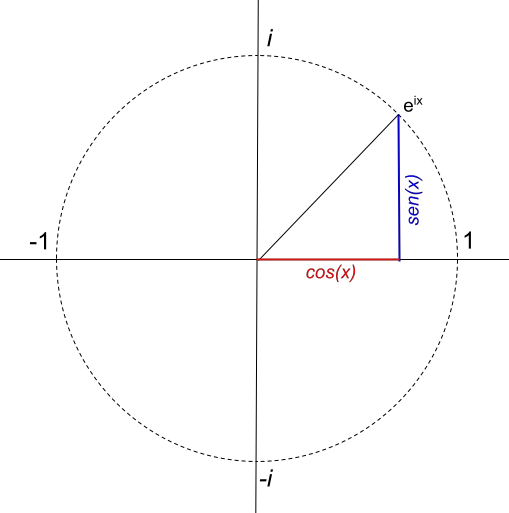
Однако радиус окружности напрямую зависит от значения модуля комплексного числа. Например, если мы хотим представить круг радиусом 4, функция будет 4e ix . Итак, функция 4e ix представляется так:
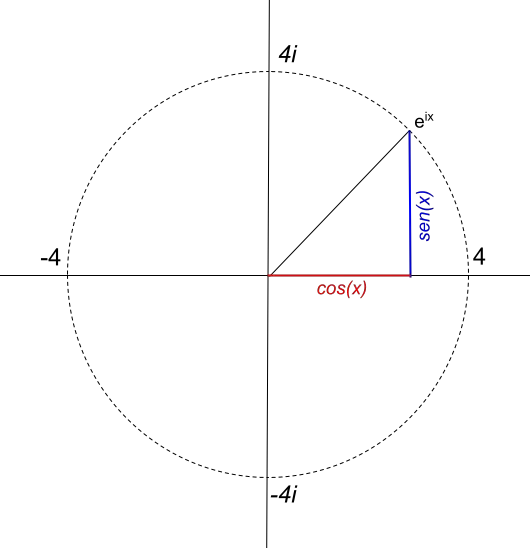
Возвращаясь к кругу радиуса 1, если мы решим представить e iπ (в радианах), мы должны сначала вычислить:
е πi = cos(π) + я sin(π)
еπi = -1 + я 0
еπi = -1
Получаем e πi = -1, что является знаменитым тождеством Эйлера.
Отсюда делаем вывод, что комплексное число e πi имеет только одну действительную часть, равную -1. Следовательно, его представление будет таким, что:
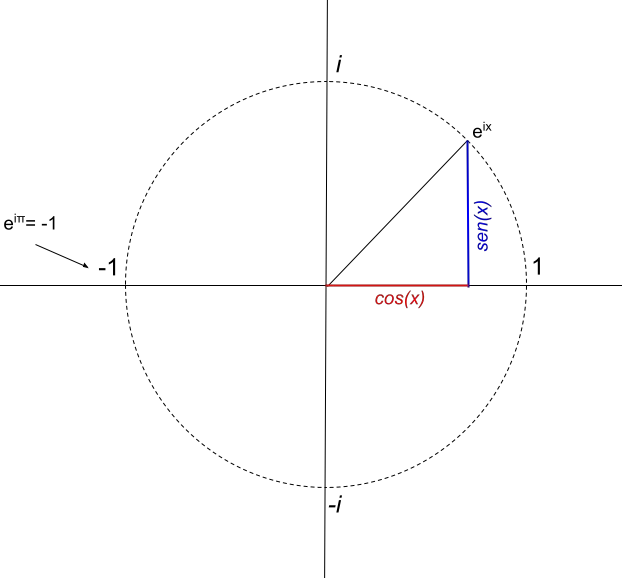
Приложения формулы Эйлера
- Комплексные числа: формула Эйлера представляет собой связь между тригонометрическими функциями и комплексными числами. Из этой формулы мы можем выражать комплексные числа разными способами: биномиальным, экспоненциальным и полярным.
- Ряд Тейлора: формула Эйлера используется для расширения функций ряда Тейлора.
- Линейная алгебра: формула Эйлера используется при диагонализации матриц, которая является фундаментальным методом линейной алгебры.
- Дифференциальное и интегральное исчисление. Формула Эйлера используется при решении дифференциальных уравнений, что является важным методом исчисления.
Кроме того, он находит применение во многих математических теориях и даже в концепциях, выходящих за рамки математической области, таких как физические теоремы.
выводы
Как вы видели в этой статье, наибольшее применение формулы Эйлера находится в комплексных числах : в их числовом выражении и в их представлении. Это правда, что это имеет некоторое применение в алгебре, но по сути вы работаете с комплексными числами. Поэтому важно, прежде всего, хорошо их понимать.
При этом мы надеемся, что помогли вам лучше понять эту концепцию. А если у вас есть вопросы или вы не знаете, как выполнять упражнение, не стесняйтесь, пишите нам в комментариях.