Вы когда-нибудь задумывались, чем рациональные числа отличаются от других чисел? В этой статье мы подробно рассмотрим рациональные числа, включая их уникальные характеристики и классификацию. Будьте готовы лучше понять концепцию!
Что такое рациональные числа?
Рациональные числа (ℚ) — это подкласс действительных чисел , включающий все числа, которые можно выразить в виде дроби. Это означает, что рациональные числа — это те, которые можно записать как отношение двух целых чисел a/b, где b ≠ 0.
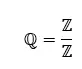
Рациональные числа также могут быть выражены как повторяющиеся или конечные десятичные числа, поскольку они состоят из серии повторяющихся цифр. Некоторые примеры рациональных чисел: 1/2, 3/4, 10/3, 2/3 и π (пи).
Подмножества рациональных чисел
Рациональные числа можно разделить на два подмножества :
- Целые числа , которые включают 0, все натуральные числа и все отрицательные числа.
- Десятичные числа или дробные числа , которые выражают значения, образованные: целой частью и десятичной частью, последняя позволяет выражать значения меньше единицы.

Другая подкатегория множества действительных чисел — иррациональные числа , которые немного сложнее.
Примеры рациональных чисел
Рациональные числа – это числа, которые можно выразить в виде дроби, то есть как частное двух целых чисел. Вот несколько примеров рациональных чисел:
-23
-4/5
-1/2
-7/9
Все дроби, представляющие целое число, одинаково рациональны. Например:
-1/1
-2/2
-3/3
Свойства рациональных чисел
Основной характеристикой рациональных чисел является то, что они всегда имеют ненулевой знаменатель.
Второе свойство этого множества состоит в том, что каждое рациональное число может быть представлено бесконечным количеством эквивалентных дробей . Например, рациональное число 3,5, равное 7/2, можно записать также 14/4, 28/8… и бесконечность других дробей.
Рациональные числа также удовлетворяют распределительному свойству . Это означает, что умножение или деление одной дроби на другую не повлияет на результат:
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (ad)/(bc)
Представление рациональных чисел
Рациональные числа можно представить несколькими способами, но наиболее распространенным является дробь . Дробь состоит из двух чисел: числителя и знаменателя.
Числитель указывает, сколько частей целого считается, а знаменатель показывает, сколько равных частей содержится в целом. Например, если торт разделить на восемь равных ломтиков и три из них съедены, доля, представляющая количество съеденного торта, будет равна 3/8.
Другой способ представления рациональных чисел — десятичные дроби . Десятичные дроби — это сокращенный способ записи дроби, где знаменателем является число 10, 100, 1000 и т. д. Например, если у вас есть 1/4 пирога, это можно выразить как 0,25 (что означает «0 целых и 25/100»).
Хотя, если мы хотим изобразить их графически, мы можем записать их и на числовой прямой , на которой очень хорошо виден порядок чисел. Далее мы покажем вам пример этой строки :
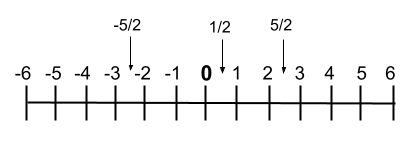
рациональные операции
Основные операции с рациональными числами такие же, как и с целыми: сложение, вычитание, умножение и деление. Если вы хотите научиться решать данный вид операций, рекомендуем прочитать нашу статью об операциях с дробями .
Однако если вы работаете с рациональными числами с десятичной основой, вы должны соблюдать порядок решения операций, который вы используете при работе с десятичными значениями .
Вывод о множестве рациональных чисел
После этого исчерпывающего объяснения можно сделать вывод, что набор рациональных чисел является одним из важнейших в математике. Он содержит все числа, которые можно представить в виде дроби, что позволяет очень точно выражать количества.