На этой странице объясняется, что такое преобразования функций и как их найти. Существует три типа трансформаций: трансляции (или смещения), симметрии и расширения (или сжатия). Вы также найдете упражнения, решаемые шаг за шагом, чтобы вы могли практиковать и понимать концепции, не оставляя никаких сомнений.
Что такое функциональные преобразования?
Иногда нас могут попросить построить графики элементарных функций, очень похожих на другие, которые мы уже знаем. Что ж, вместо повторного представления аналогичной функции можно использовать методы для легкого и быстрого переключения от представления одной функции к другой.
Таким образом, преобразования функций — это приемы, позволяющие посредством элементарных операций перейти от графического представления функции к графическому представлению другой очень похожей функции.
В основном различают три типа преобразований элементарных функций:
- Переводы или перемещения : функцию можно перемещать по вертикали и горизонтали.
- Отражения или симметрии . Функция может быть отражена с использованием оси X или оси Y в качестве оси симметрии.
- Расширение и сжатие : функцию можно увеличить или уменьшить.
Как только мы увидим концепцию преобразования функции, мы углубимся в каждый тип модификации.
Переводы или перемещения функций
Начнем со смены функций. Существует два типа: вертикальные переводы и горизонтальные переводы.
Перевод или вертикальное перемещение функции
Чтобы перевести или переместить функцию по вертикали (вдоль оси Y), необходимо добавить к функции или вычесть константу:
Мы перемещаем функцию на k единиц вверх , добавляя к функции ka:
Сместим функцию на k единиц вниз , вычитая из функции ka:
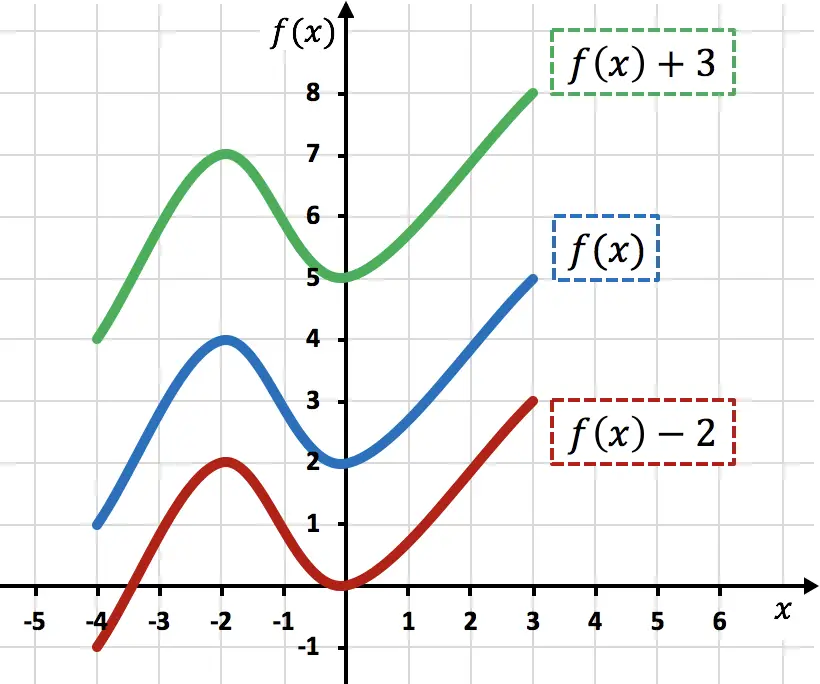
Как видно из графика, добавление константы к любой функции сдвигает добавляемые единицы вверх (зеленая функция). С другой стороны, при вычитании числа из функции вычитаемые единицы перемещаются вниз (красная функция).
Обратите внимание, что при этом типе движений изменяются только координаты Y функциональных точек, а координаты X остаются прежними.
Трансляция или горизонтальное перемещение функций
Чтобы перевести или сдвинуть функцию по горизонтали (вдоль оси X), необходимо добавить или вычесть константу к независимой переменной x :
График
это график
переместился на k единиц влево.
График
это график
сдвинуто на k единиц вправо.
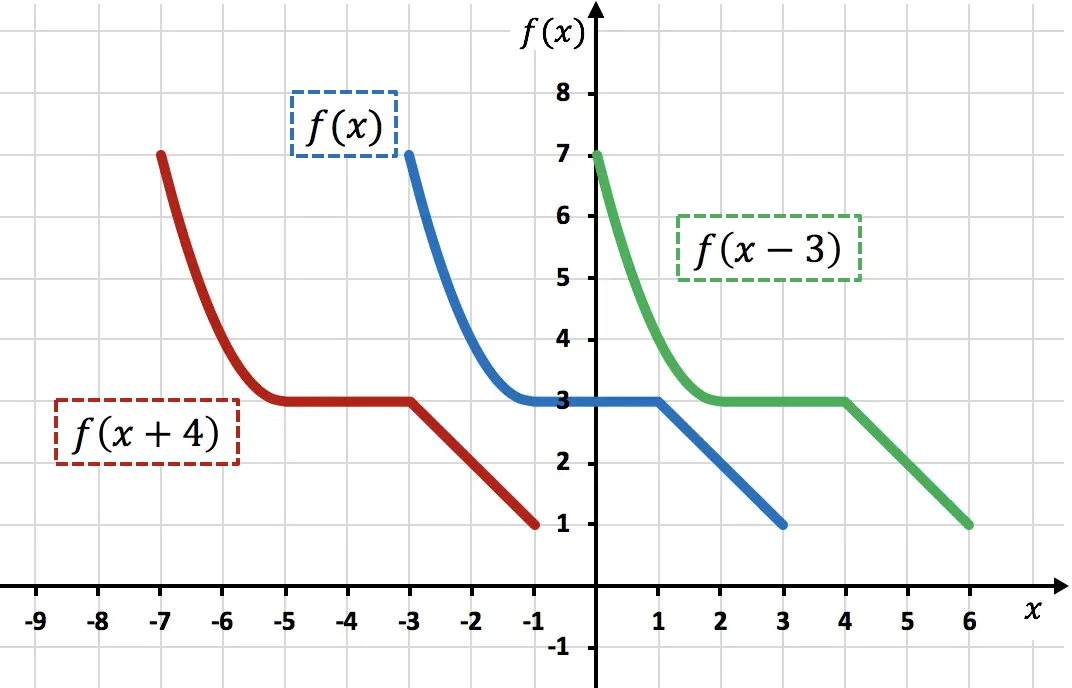
Как видно из графика, при добавлении константы непосредственно к переменной x функция сдвигает добавленные единицы влево (красная функция). С другой стороны, при вычитании числа из переменной x функция сдвигает вычитаемые единицы вправо (зеленая функция).
Обратите внимание, что при этом типе движений изменяются только координаты X функциональных точек, а координаты Y продолжают иметь то же значение.
Пример перевода или перемещения функции
- Переместите следующую функцию на 4 единицы вверх и на 3 единицы вправо:
Чтобы переместить функцию на 4 единицы вверх, нам нужно добавить к функции 4 единицы:
А чтобы еще и сдвинуть функцию на 3 единицы вправо, надо вычислить
. Поэтому там, где есть
мы можем
Таким образом, функция, сдвинутая на 4 единицы вверх и на 3 единицы вправо, равна:
Ниже приведены графики исходной функции и преобразованной функции, чтобы вы могли увидеть разницу между ними:
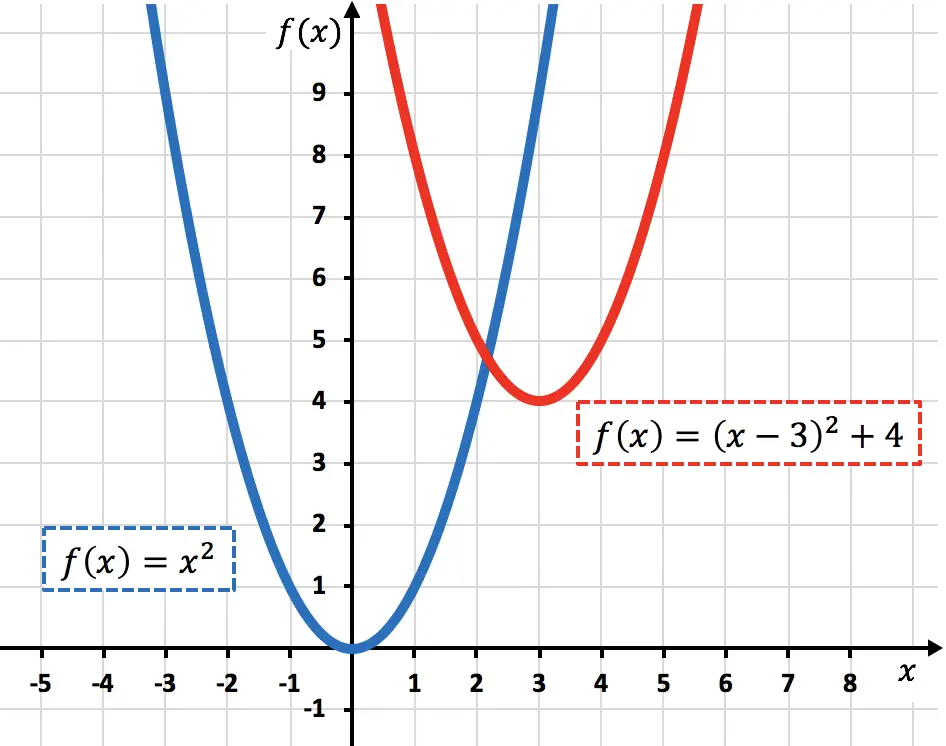
Некоторые математики называют косое перемещение или поступательное движение, когда оба типа движения происходят одновременно.
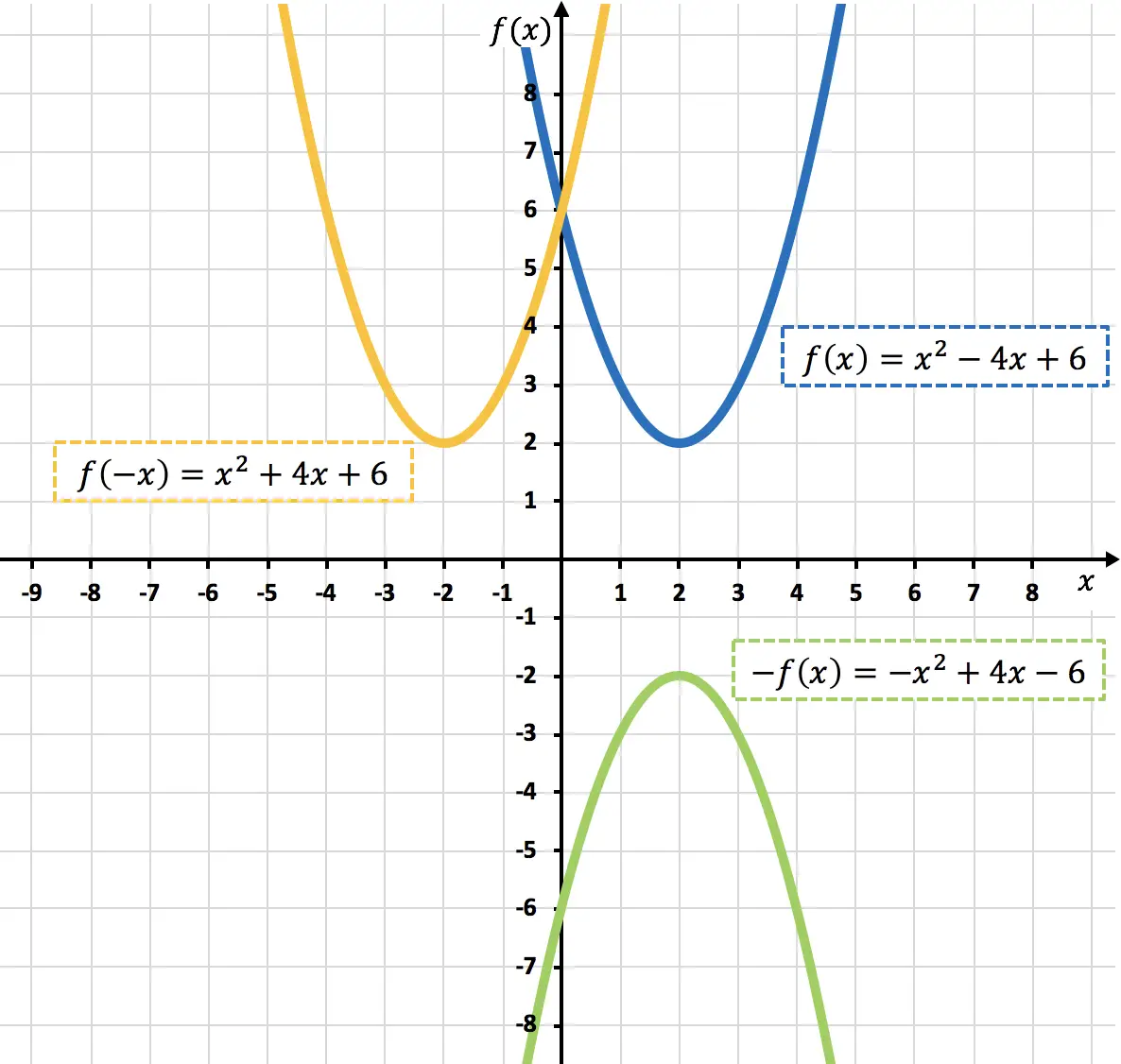
Отражение или симметрия функции относительно осей координат.
Мы можем представить симметричную функцию относительно любой декартовой оси следующим образом:
Чтобы отразить функцию относительно оси х, нам нужно изменить знак функции, то есть нужно вычислить
Чтобы отразить функцию относительно оси y, мы должны инвертировать независимую переменную x , то есть мы должны вычислить
Как видно на предыдущем графике, умножая функцию на -1, мы графически инвертируем ее (оранжевая функция), или другими словами, зеркально отображаем ее относительно оси X.
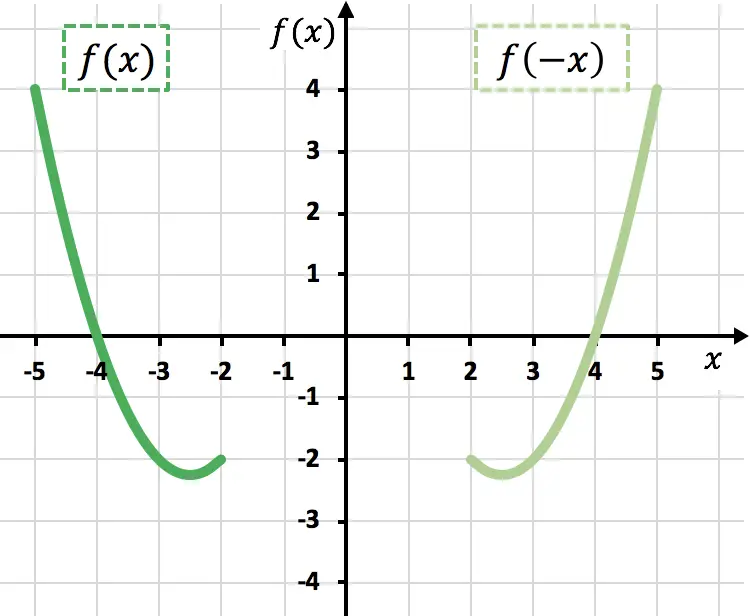
Как видно на предыдущем графике, отрицая переменную x , мы зеркально отображаем функцию относительно оси Y (светло-зеленая функция).
Пример зеркального отображения функции
- Вычислите симметричную функцию относительно оси OX и симметричную функцию относительно оси OY следующей квадратичной функции:
Чтобы найти функцию, симметричную относительно оси X, необходимо сделать
:
![-f(x)=-\bigl[x^2-4x+6\bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec1ca457c73589ee30ad6641f0d66c10_l3.png "Rendered by QuickLaTeX.com")
И чтобы найти функцию, симметричную относительно оси Y, мы должны сделать
. Поэтому заменяем там, где есть
в исходной функции слагаемым
Ниже вы представили как исходную функцию, так и найденные симметричные функции:
Расширение и сокращение функций
Как и в случае с переводом, существует два типа расширения или сжатия: вертикальное и горизонтальное.
Вертикальное расширение и сжатие функции
Умножив целочисленную функцию на коэффициент, мы можем заставить ее расширяться или сжиматься:
Чтобы расширить (или расширить) функцию по оси Y, нам нужно умножить ее на число больше 1:
Чтобы уменьшить функцию по оси Y, нам нужно умножить ее на положительное число меньше 1:
Чтобы уменьшить функцию по оси X, нам нужно умножить все x на число больше 1:
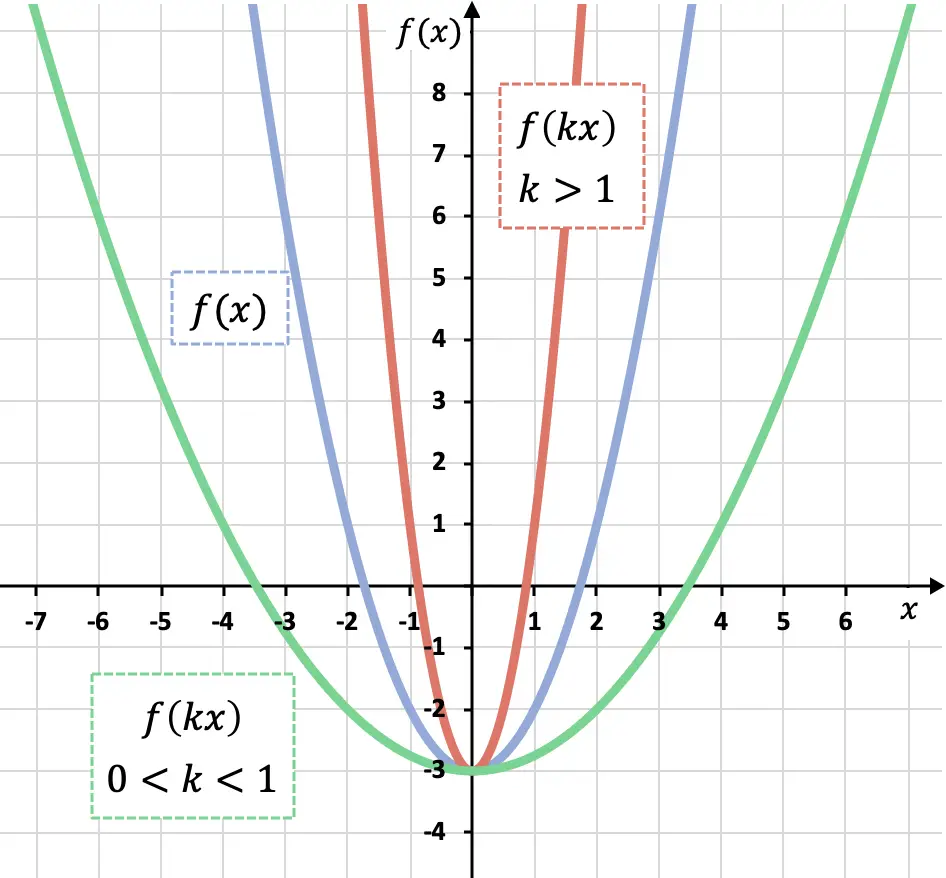
Как вы можете видеть на предыдущем графике, если мы умножим все x функции на коэффициент больше 0, но меньше 1 (зеленая функция), мы увеличим ее по оси OX, с другой стороны, если мы умножим функцию с коэффициентом больше 1 (красная функция) уменьшаем по оси ОХ.
Пример того, как развернуть или свернуть функцию
- Продублируйте следующую иррациональную функцию по вертикали и по горизонтали:
Чтобы расширить функцию по оси Y на два, мы должны умножить всю функцию на 2:
А чтобы также расширить функцию на два по оси X, мы должны умножить все x функции на
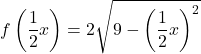
Таким образом, функция, дублированная на двух координатных осях:
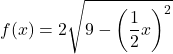
Ниже вы видите исходную функцию и преобразованную функцию, представленную графически, чтобы вы могли увидеть различия между ними:
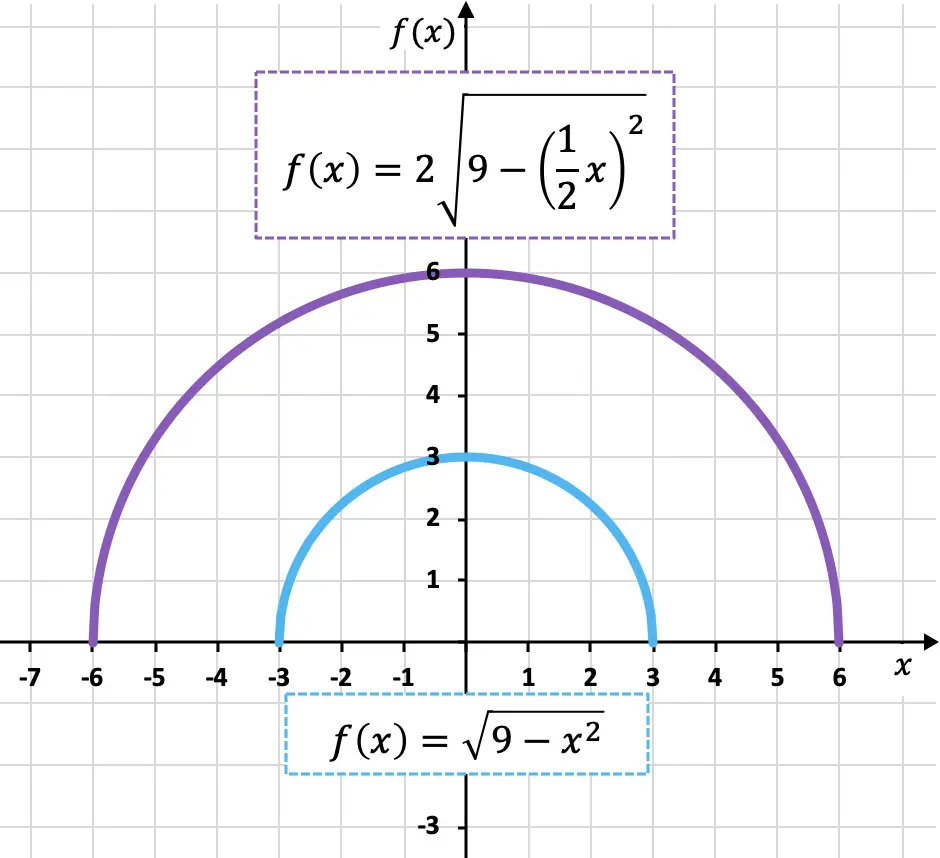
Как видите, новый объект (фиолетовый цвет) в два раза больше исходного объекта (синий цвет) как по вертикали, так и по горизонтали, поэтому объект расширился.
Решенные упражнения на преобразования функций
Упражнение 1
Переместите следующую функцию третьей степени на 5 единиц вверх:
Чтобы переместить функцию на 5 единиц вверх, добавьте 5 к функции:
![\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d29d1537293d975f7fbda8871622660f_l3.png "Rendered by QuickLaTeX.com")
Таким образом, функция, сдвинутая на 5 единиц, равна:
Упражнение 2
Найдите симметричную функцию относительно оси Y следующей квадратичной функции:
Чтобы найти функцию, симметричную относительно оси Y, необходимо вычислить
, то есть нам нужно заменить
Для
в функции:
Таким образом, симметричная функция относительно оси OY равна:
Упражнение 3
Выполните горизонтальное сжатие следующей функции до одной трети ее представления:
Чтобы уменьшить функцию через
Таким образом, приведенная функция имеет вид:
Упражнение 4
Вычислите симметричную функцию относительно оси OX следующей функции, переведенной на 4 единицы вправо:
Прежде чем вычислить симметричную функцию, мы должны сначала переместить функцию на 4 единицы вправо, поэтому:
И как только мы переместили функцию, мы вычисляем симметричную функцию относительно оси X. Для этого надо инвертировать полученную функцию:
![\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-62a7ea0e19503ec030dcdaa59c9157eb_l3.png "Rendered by QuickLaTeX.com")
Короче говоря, функция после применения всех элементарных операций выглядит так:
Упражнение 5
Сместите следующую функцию на 2 единицы влево, затем расширьте ее по вертикали в 4 раза:
Сначала переместим функцию на две единицы влево:
А затем разложим функцию по оси Y в 4 раза:
![4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]](https://mathority.org/wp-content/ql-cache/quicklatex.com-07175c64db9d7e8074852df8944df6c4_l3.png "Rendered by QuickLaTeX.com")
В заключение, функция после применения всех элементарных преобразований имеет вид:
Упражнение 6
Из функции
определить, какое из представлений на графике соответствует функции
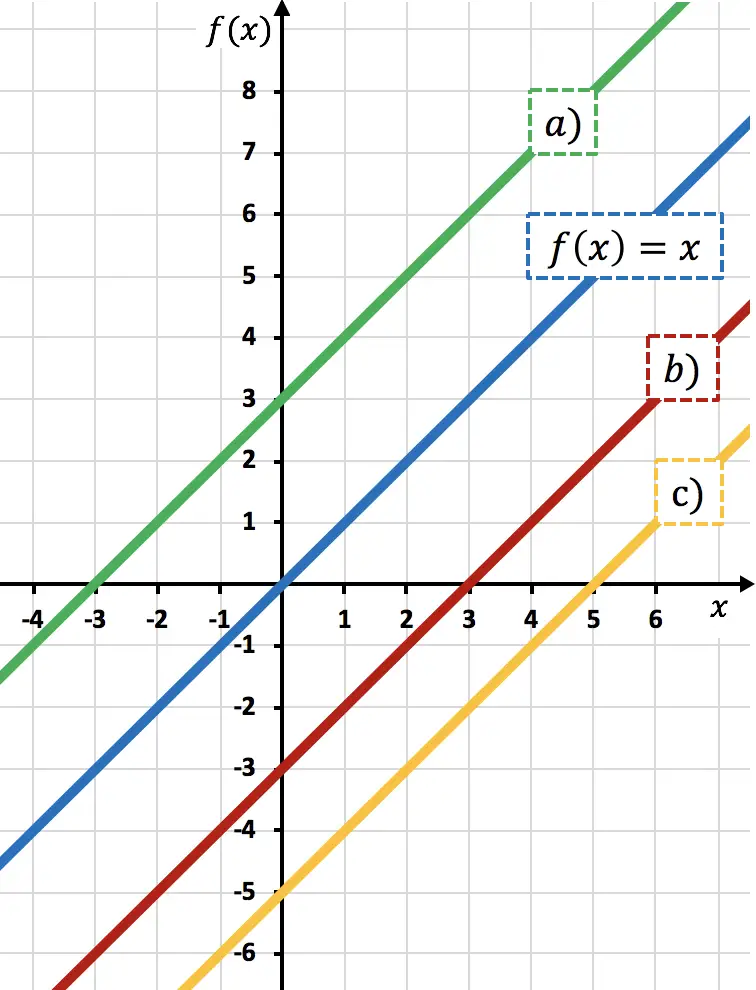
Функция
это функция
переместился на 3 единицы вниз. Потому что, вычитая число из функции, вы перемещаете функцию вниз.
Таким образом, представление
соответствует линии b) , так как она сдвинута на 3 единицы вниз по сравнению с
Это можно увидеть, взглянув на вертикальную ось: когда
проходит через 0, красная линия проходит через -3, поэтому она смещается на 3 единицы вниз.
Упражнение 7
Из функции
определить, какая парабола является представлением функции
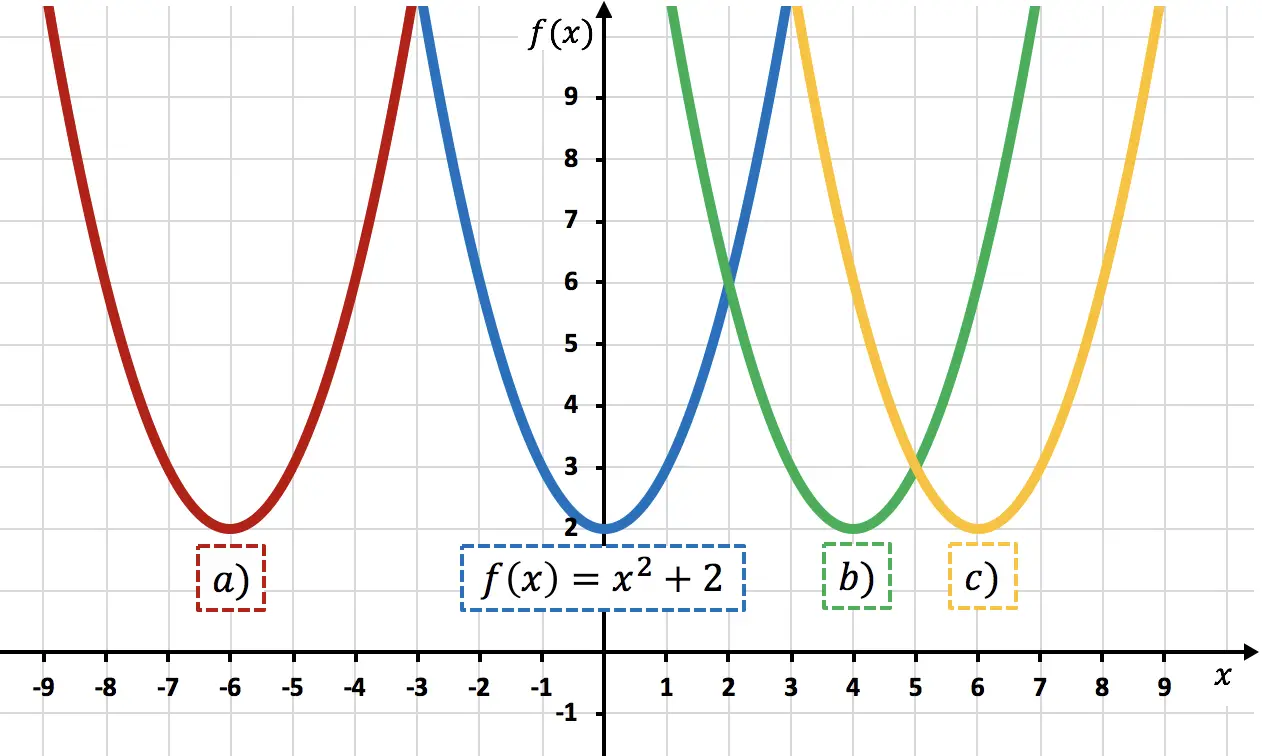
Функция
это функция
сдвинуто на 6 единиц вправо. Мы можем убедиться в этом, вычислив
Таким образом, представление
соответствует параболе в) , поскольку она сдвинута на 6 единиц вправо по сравнению с
.
В этом можно убедиться, посмотрев на вершины парабол: расстояние между вершинами параболы
а вершина параболы в) равна 6 единицам, поэтому последняя сдвинута на 6 единиц вправо по сравнению с первой.