В этой статье мы рассмотрим понятия, необходимые для понимания того, что такое полный полином . Кроме того, мы узнаем, как он используется и почему это такая важная идея для манипулирования и количественной оценки полиномов. Хотя в первую очередь очень рекомендуется прочитать нашу статью о полиноме .
Что такое полный полином?
Полный многочлен — это алгебраическое выражение , состоящее из суммы слагаемых. Каждый член образуется путем умножения числа, называемого коэффициентом, на степень x. Наивысшая степень многочлена называется степенью многочлена, а наименьшая (x, возведенная в ноль) называется независимым членом.
Отсюда мы определяем полный многочлен как тот, который включает в себя члены всех возможных степеней вплоть до степени многочлена . Другими словами, если многочлен имеет степень 5, то он должен включать члены степени 5, 4, 3, 2, 1 и 0. Другими словами, полным многочленом является тот, который не имеет нулевых членов (равных нулю ).
На следующем изображении вы можете увидеть пример этого. Как можно видеть, в нем есть член для каждого показателя x, от x в степени четырех (четыре — это степень многочлена) до x в степени нуля, в независимом члене. Следовательно, этот многочлен соответствует определению полного многочлена.
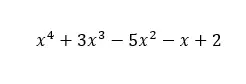
С другой стороны, если у нас есть другой многочлен, подобный показанному на следующем изображении, мы будем иметь дело с неполным многочленом . Поскольку два члена отсутствуют, значение x увеличивается до двух и независимого члена. А из определения полного многочлена, если отсутствует хотя бы один член, многочлен перестает быть полным.
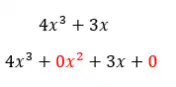
Примеры полных полиномов
Теперь, когда вы знаете определение полного полинома, давайте рассмотрим несколько примеров из реальной жизни . Мы начнем с рассмотрения полного многочлена степени 2, еще одного — степени 4 и, наконец, одного — степени 6. Очевидно, мы могли бы привести примеры гораздо более высоких степеней, но идея одинакова для всех типов многочленов.
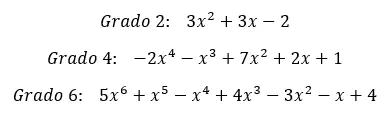
Эти примеры дают очень ясное определение полных полиномов. Вот почему теперь мы можем перейти на следующий уровень. В следующем разделе мы подробно опишем два типа существующих полных полиномов в соответствии с порядком членов. Многие студенты воспринимают это как нечто само собой разумеющееся, но приятно увидеть это снова.
Типы полных полиномов
Мы можем разделить полные полиномы на два типа: упорядоченные полные полиномы и неупорядоченные или неупорядоченные полные полиномы. Первые характеризуются структурой, члены которой упорядочены по степеням х. Начиная с высшей степени и заканчивая термином независимый.
Хотя это полный неупорядоченный полином, он выражается членами в случайном порядке . Следовательно, вы можете найти член с наибольшим показателем рядом с независимым членом. Но такой способ выражения многочлена непрактичен, поэтому мы рекомендуем всегда использовать упорядоченные многочлены .
Далее мы покажем вам пример каждого типа, чтобы вы могли в полной мере оценить разницу.
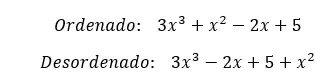
Мы надеемся, что эта статья помогла вам понять концепцию полных полиномов. Если у вас есть вопросы, смело оставляйте их в комментариях.