Полиномиальные функции

В этой статье вы найдете очень подробное объяснение полиномиальных функций , дополненное примерами. Кроме того, вы сможете увидеть, как полиномиальные функции используются в повседневной жизни, благодаря упражнениям, которые мы вам представим в конце.

Что такое полиномиальная функция?

Полиномиальные функции или полиномиальные функции — это функции, которые задаются алгебраическим выражением, эквивалентным многочлену . Это означает, что выражение должно следовать структуре многочлена: f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ , в зависимости от структуры которого мы будем определить тип полиномиальной функции, которую мы собираемся обрабатывать. Другая очень важная характеристика этих функций состоит в том, что все их показатели неизвестных являются целыми и положительными .

Части полиномиальной функции

Мы можем выделить три важных элемента, касающихся этих функций:

• Полиномиальные коэффициенты: это числа, которые сопровождают неизвестные, например, 3 в следующем члене является коэффициентом: 3x ² . Следует отметить, что коэффициентов столько, сколько слагаемых в многочлене.
• Экспоненты или индексы многочлена: это степени неизвестных, например, 2 в следующем члене является показателем: 3x ² . И как мы уже объяснили, в случае полиномиальной функции они всегда будут положительными и целыми.
• Степень многочлена: это значение эквивалентно показателю степени наивысшей степени среди всех членов, составляющих многочлен. В случае многочлена f(x) = ^3×2 – 4x+2 степень равна двум.

Как узнать, является ли функция полиномиальной или нет?

Чтобы идентифицировать полиномиальную функцию, мы должны посмотреть, соответствует ли она характеристикам, о которых мы только что говорили. Мы начнем с проверки, имеет ли выражение, определяющее функцию, полиномиальную структуру : f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ . А затем мы проверим, что индексы являются положительными и целыми. С помощью этих простых шагов мы сможем определить, является ли функция полиномиальной или нет.

Типы полиномиальных функций с примерами

Далее мы покажем вам различные типы существующих полиномиальных функций , которые классифицируются в зависимости от степени полинома. Кроме того, вы найдете пример графического представления для каждого типа. Благодаря этим примерам полиномиальных функций вы сможете лучше увидеть различия между различными категориями.

постоянные функции

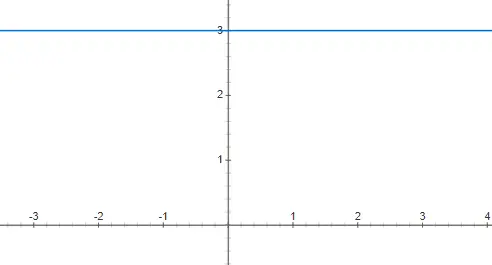
Постоянные функции эквивалентны многочлену нулевой степени, это означает, что коэффициент при x равен 0. Именно поэтому функции этого типа не зависят от значения независимой переменной x. Поэтому его графическое представление представляет собой горизонтальную линию, которая бесконечна. Ниже вы можете найти представленный пример f(x) = 3:

полиномиальные функции первой степени

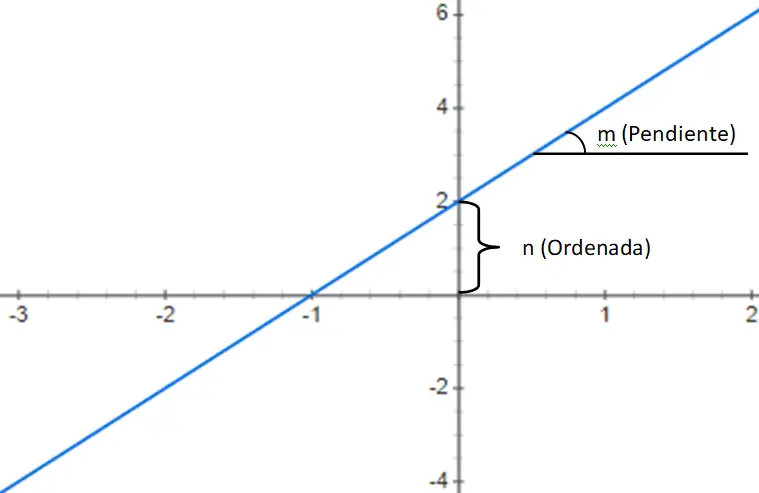
Во-вторых, мы находим полиномиальные функции первой степени , которые задаются полиномом первой степени со следующей структурой: f(x) = mx + n. Это выражение состоит из числа, называемого наклоном (m), которое умножает переменную xy на константу (n), которая добавляется к этому произведению. Итак, исходя из значений m и n, мы можем выделить три разных типа функций:

• Аффинные функции: этот подтип характеризуется наличием значения n, отличного от 0, то есть значение компьютера отличается от 0. Следовательно, этот тип функции не проходит через точку (0, 0), также называемую Происхождение. Также прокомментируйте, что если m < 0, функция будет убывающей, а если m > 0, функция будет возрастать.
• Линейные функции. Единственное отличие этих функций от аффинных функций заключается в том, что n = 0, поэтому у них нет компьютера. Следовательно, выражение для линейных функций эквивалентно f(x) = mx. Этот тип довольно легко изобразить, так как он всегда проходит через точку (0, 0) и по наклону мы уже получаем график.
• Функции тождества: этот последний тип представляет собой подгруппу линейных функций, у которых an = 0 и m = 1. Это означает, что выражение остается f(x) = x, при этом графическое представление представляет собой диагональ, образующую угол 45° с одна из осей. Этот тип функции также проходит через начальную точку (0, 0).

Ниже вы найдете пример полиномиальной функции первой степени, точнее, аффинной функции f(x) = 3x + 2:

квадратичные функции

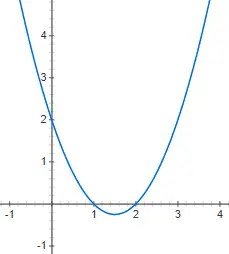
Квадратичные функции или квадратичные функции выражаются с помощью квадратичных многочленов, которые следуют структуре: f(x) = ax ² + bx + c, где a отлично от 0. В этом случае графическое представление значительно сложнее, так как уже не прямая линия, а вертикальная парабола . Ниже вы можете найти представление квадратичной функции f(x) = 2x ² + 4x – 1:

кубические функции

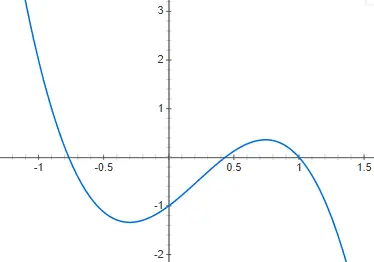
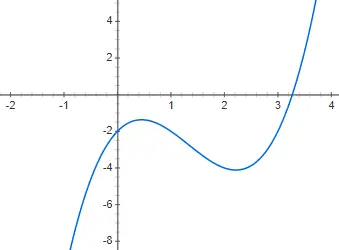
Кубические функции или функции третьей степени задаются полиномом третьей степени: f(x) = ax ³ + bx ² + cx + d, отличным от 0. Представление функции этого типа еще сложнее, чем второй степени, поскольку она может иметь несколько различных форм. Хотя основной формой или, по крайней мере, наиболее распространенной, является та, которую мы собираемся показать вам в следующем примере: f(x) = 2x ³ – 4x ² + 2x – 2:

Свойства полиномиальных функций

Полиномиальные функции обладают рядом свойств или характеристик , которые отличают их от других функций, и ниже мы опишем их как можно более подробно. Таким образом, когда вы увидите подобные функции, вам будет очень легко их идентифицировать:

• Область определения полиномиальной функции равна всем действительным числам : Dom f = R или Dom f = (-∞, ∞), поэтому они непрерывны во всем наборе действительных чисел.
• Точка его пересечения на оси Y эквивалентна (0, a ₀ ), где ₀ является независимым членом.
• Разрезает по оси X количество раз, равное или меньшее степени многочлена.
• Полиномиальные функции не имеют асимптот.
• Если показатель степени всех членов нечетен, то график симметричен относительно начала координат, а если показатель степени всех членов четен, он симметричен относительно оси OY.
• Число точек перегиба функции этого стиля равно или меньше n – 2, где n – степень.
• Число относительных максимумов и минимумов функции этого стиля равно или меньше n – 1, где n – степень.

Как анализировать полиномиальную функцию?

Чтобы проанализировать полиномиальную функцию, мы должны следовать той же процедуре, которую мы использовали бы для анализа любой другой функции. В следующем списке мы суммировали различные элементы, которые необходимо изучать или лечить:

• Домен и диапазон
• Точки пересечения с горизонтальной и вертикальной осями
• Монотонность (нарастание и убывание, максимумы и минимумы)
• Кривизна (в функциях степени больше единицы)

Очевидно, мы можем вывести анализ на другой уровень и изучить множество других элементов, хотя этого должно быть достаточно. Так как, зная эти элементы, вы будете иметь четкое представление о том, как выглядит функция, и сможете представить ее графически.

Упражнения с полиномиальными функциями

Далее мы предлагаем вам серию упражнений на практику представления функций , в частности полиномиальных функций. Таким образом вы закрепите все понятия, изложенные в этой статье:

Упражнение 1

Постройте график следующей полиномиальной функции первой степени f(x) = x + 2 и скажите, какого она типа:

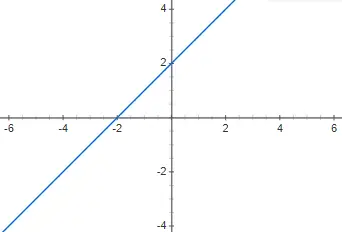
Это аффинная полиномиальная функция первой степени, поскольку она отличается от 0, а m отличается от 0.

Упражнение 2

Постройте график следующей квадратичной полиномиальной функции f(x) = x ² + x – 2:

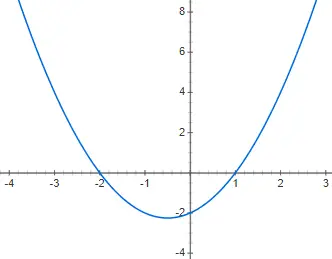
Упражнение 3

Постройте график следующей полиномиальной функции третьей степени f(x) = x ² + x – 2: