Несократимая дробь — это дробь, которую нельзя упростить дальше, поэтому она не имеет меньших эквивалентных дробей . Другими словами, НКО числителя и знаменателя неприводимой дроби равен 1, поскольку других общих делителей у них нет. Например, выражение «5/8» уже нельзя сократить, поэтому мы говорим, что оно находится в простейшей форме или что оно несократимо.
Калькулятор несократимых дробей
Прежде чем продолжить теорию, мы хотим показать вам калькулятор, который позволит вам получить несократимую дробь любого смешанного числа. Все, что вам нужно сделать, это ввести значения числителя и знаменателя и нажать «Упростить дробь» , после чего вы получите уменьшенную форму в поле результата. Мы рекомендуем использовать этот инструмент, чтобы сразу упростить любую дробь или даже исправить упражнения с дробями.
Что такое несократимая дробь и как ее вычисляют?
Как мы уже объясняли вначале, несократимая дробь — это дробь, которую нельзя упростить дальше, поэтому это непосредственная дробь . Если вы хотите найти этот вид дробей, вам придется воспользоваться упрощением дробей , таким образом вы найдете эквивалентную дробь, несократимую по отношению к исходной дроби. По этой последней ссылке вы можете найти подробное руководство по упрощению дробей, хотя в следующем списке мы кратко объясняем эти шаги:
- Нахождение общих множителей: Для начала вам нужно найти наибольший общий делитель числителя и знаменателя. Таким образом вы получите число, которое позволит уменьшить оба значения, сохранив эквивалентность.
- Разделите сокращаемую дробь на НКО. Если у вас есть НКО, вам нужно будет разделить числитель и знаменатель на этот общий делитель. Это даст вам более простой (или меньший) эквивалентный числитель и знаменатель.
Вы также можете использовать другие методы для нахождения несократимых дробей, которые описаны в нашей статье об упрощении дробей. Хотя с помощью этой методики, которую мы вам объяснили, вы можете очень легко и быстро уменьшить любую дробь, какую захотите.
Пример сокращаемых дробей и несократимых дробей
На следующем изображении вы можете найти четыре примера сокращаемых дробей и еще четыре несократимых дроби. Рекомендуем вам попробовать упростить каждую из дробей, так вы будете четко понимать разницу между двумя видами дробей.
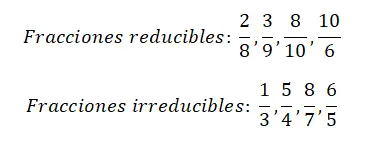
Пример расчета несократимой дроби
Здесь мы шаг за шагом покажем вам, как можно упростить дробь двумя способами. В первом показана полная процедура, которую мы объяснили в предыдущем разделе. А второй показывает несколько иную систему, которая предполагает деление числителя и знаменателя на одно и то же значение, начиная с наименьших делителей (не считая 1) и двигаясь вверх. Однако, если вы считаете, что вторая система слишком сложна, вы можете ее игнорировать.
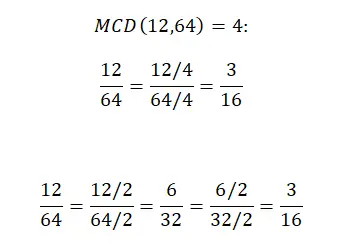
Несократимая дробь десятичного числа
Несократимая дробь, полученная из десятичного числа, называется производящей дробью . Важно отметить, что она рассчитывается по-разному в зависимости от типа десятичной дроби, с которой мы имеем дело (точная, чисто периодическая или смешанная периодическая). Следующий пример наглядно демонстрирует это математическое понятие: 5/7 = 0,7142857 . Как видите, пять седьмых – это несократимая дробь, эквивалентная десятичному числу 0,7142857…
Как узнать, является ли дробь неприводимой?
Чтобы узнать, является ли дробь сократимой или несократимой, можно воспользоваться двумя способами. Первый – вычислить наибольший общий делитель числителя и знаменателя, если это значение отлично от единицы, то это будет означать, что это сокращаемая дробь. И если в результате вы получите такую, то знайте, что дробь будет несократимой. Во-вторых, для выполнения подобных проверок вы можете использовать калькулятор несократимых дробей, который мы показали вам вначале.
Решенные упражнения на несократимые дроби
Теперь, когда вы прочитали теорию, рекомендуем вам попробовать решить эти задачи , что позволит вам попрактиковаться в вычислении несократимых дробей. Кроме того, если вы хотите улучшить свое понимание смешанных чисел, мы рекомендуем попробовать решить эти упражнения с дробями . Благодаря чему вы лучше поймете само понятие дроби.
Упражнение 1
Вычислите несократимую долю следующих сокращаемых дробей. Помните, что для упрощения дробей можно использовать любой метод. А когда вы закончите упражнение, вы сможете сравнить свои результаты с теми, которые мы покажем вам на изображении ниже.
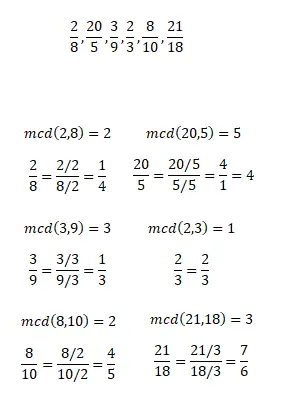
Упражнение 2
Назовите дроби, эквивалентные несократимым дробям 2/3 и 4/5. Для выполнения этой задачи рекомендуем посмотреть на числа в числителе и знаменателе и подумать, какое отношение делимости у них имеется. Возможно, вы сможете использовать наибольший общий делитель или наименьшее общее кратное, чтобы найти то, что ищете...
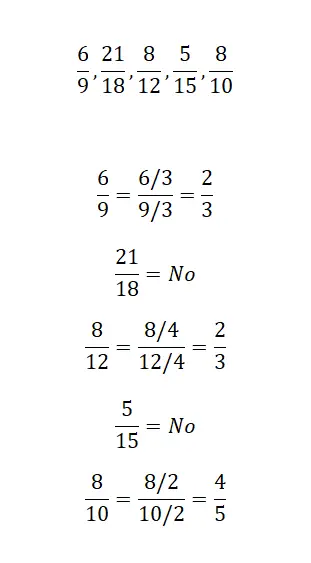
Упражнение 3
В этом последнем упражнении вам нужно только указать, имеют ли следующие три дроби одну и ту же несократимую дробь. Поэтому необходимо максимально сократить три фракции и проанализировать результат. Решив задачу, вы сможете сравнить свои решения с нашими.
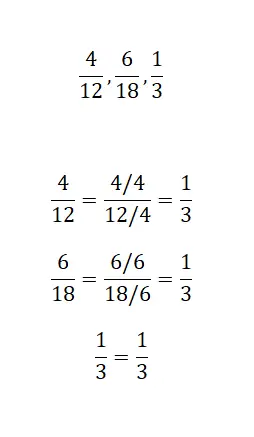
Дополнительная информация о дробях
Мы надеемся, что эта статья помогла вам разобраться в несократимых дробях. Хотя если у вас возникнут вопросы, смело прочтите наше объяснение дробей . Там вы найдете всю информацию о дробях: определение, категории, действия и упражнения, все объяснено с использованием теории и примеров. Уверяем вас, что если вы прочитаете эту статью, вы избавитесь от многих принципиальных сомнений, связанных с этой темой.