Упрощение дробей или сокращение дробей — это математическая процедура, целью которой является преобразование сложной дроби в другую, более простую эквивалентную дробь . Следовательно, это позволяет найти неприводимую дробь исходного выражения, причем сделать это можно несколькими способами. Однако, прежде чем объяснять их, мы рекомендуем вам попробовать калькулятор упрощения дробей, который вы можете найти чуть ниже этого текста.
Онлайн фракция Упростить
С помощью следующего онлайн-калькулятора упрощения дробей вы сможете уменьшать смешанные числа любого типа. Проще говоря, вы должны ввести значения числителя и знаменателя, а затем нажать кнопку «Упростить». Сделав это, вы получите максимально упрощенное выражение.
Как упростить дробь?
Как мы уже говорили, упрощение дробей предполагает нахождение несократимой части более сложной дроби. В настоящее время у нас есть два метода упрощения дробей: первый — использовать обычное деление, а второй — извлечь общий делитель.
Упростить дроби делением
Эта система состоит из деления числителя и знаменателя на общие делители (кроме 1) до тех пор, пока у нас не останется общий делитель, таким образом у нас будет несократимая дробь. Хотя выбрать делитель, который мы будем использовать при каждом делении, мы можем сделать это двумя разными способами: первый — использовать общие делители, пока не получим простейшую форму этой дроби, а второй — вычислить наибольший общий делитель дроби. числитель и знаменатель.
Например, если мы хотим упростить дробь 12/64, мы можем сделать это, разделив числитель и знаменатель на gcf обоих, или разделив обе части дроби на одно и то же число, пока не получим несократимую дробь, начиная с с наименьшими делителями (не считая 1) и идущими вверх. Ниже вы можете увидеть оба метода, решенные шаг за шагом:
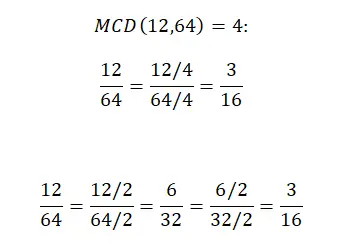
Упрощение дробей путем выделения общего фактора
Чтобы реализовать этот другой метод, нам придется разложить числитель и знаменатель на простые числа . И подставим исходные числовые значения в произведение эквивалентных степеней . Далее мы приступим к сокращению выражения путем упрощения степеней с общим основанием, используя свойства степеней. Теперь мы упростим пример дроби, используя этот метод:
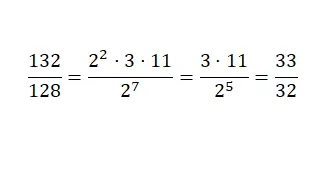
Дроби, которые трудно сократить
Далее мы разрешим некоторые сомнения относительно наиболее сложных случаев упрощения, таким образом вы сможете уменьшить любую предложенную вам дробь. Хотя этот раздел является необязательным, если вы хотите начать практиковаться, вы можете перейти к последнему разделу:
Упрощение дробей с показателями
Чтобы упростить этот тип дробей, нам нужно записать выражение показателя степени в виде одного числового значения. Во-первых, мы можем попробовать факторизацию простых чисел , упростив числитель и знаменатель. И тогда, если мы еще не получили неприводимую дробь, продолжим делить две части дроби до тех пор, пока не получим выражение, которое уже невозможно сократить. Как видите, упрощение дробей с помощью степеней предполагает объединение всех методов, о которых мы говорили в предыдущем разделе.
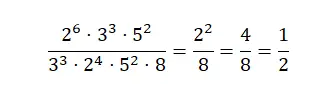
упростить отрицательные дроби
Когда мы хотим упростить отрицательные дроби, мы можем сделать это с помощью одного из трех методов, описанных ранее, поскольку знак не влияет напрямую на процедуру расчета . Вам нужно внести только одно изменение в результат — добавить отрицательный знак. Но все остальное точно так же. Чтобы вы могли это увидеть, ниже мы покажем вам первый пример, который мы объяснили, решенный, но с отрицательным знаком.
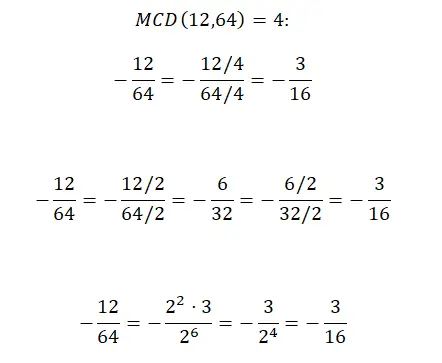
Упрощение дробей с большими числами
В этом случае мы рекомендуем использовать метод извлечения общих множителей , поскольку большие числа становятся проще, если выразить их в простых множителях. Таким образом, вы избавляете себя от необходимости решать множество делений, пока не придете к несократимой дроби. Хотя на самом деле вы можете использовать любой метод, который вам больше нравится.
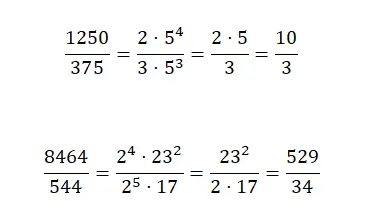
Как упростить дроби с помощью научного калькулятора?
Во многих научных калькуляторах мы можем выразить любую дробь более простым способом, если только она не является неприводимой. В случае научных калькуляторов Casio (самая распространенная марка среди студентов) необходимо нажать кнопку, отмеченную следующим выражением «S⇔D». Благодаря этому мы сможем упрощать выражения всех типов , включая дроби . У других марок также есть способы сделать это, но вам придется ознакомиться с этим в руководстве к вашей модели, поскольку дальнейшая процедура может немного отличаться.

Решенные упражнения на упрощение дробей
Вот несколько упражнений по упрощению дробей, с помощью которых вы сможете попрактиковаться в различных методах, которые мы объяснили. Мы рекомендуем вам отнестись к теоретической части с такой же важностью, как и к практике, поскольку именно благодаря ей вы прекрасно поймете математические концепции, задействованные в упражнениях этого типа.
Упражнение 1
Упростите следующие дроби, пока не найдете несократимую дробь:
На следующем изображении вы найдете четыре дроби, упрощенные одним из трех методов. Хотя, когда вы пытаетесь уменьшить их самостоятельно, вы можете сделать это тем методом, который вам больше нравится, главное, чтобы вы получили правильный результат, который вам следует сравнить с тем, который мы покажем вам в коррекции:

Упражнение 2
Рассчитайте значение x в следующих уравнениях дробей:
Приведем теперь два уравнения с дробями, которые можно решить путем упрощения. Это немного более сложное упражнение, но, применив некоторые основные математические понятия, а также те, которые мы объяснили в этой статье, вы сможете легко его решить.
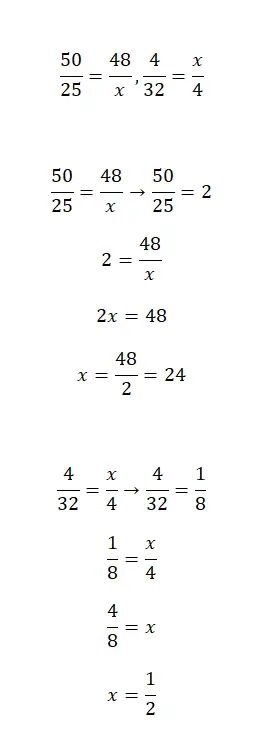
Упражнение 3
Вычислите эквивалентные несократимые доли каждой из дробей, показанных ниже:
Теперь мы предлагаем вам максимально упростить эти дроби, пока вы их решаете, вы увидите, что они немного сложнее предыдущих. Поскольку один включает отрицательный знак, другой включает большие числовые значения, а третий включает степени.

Если вы хотите больше упражнений с дробями, рекомендуем перейти по этой последней ссылке, там вы найдете множество задач и операций с дробями. С помощью которого вы сможете практиковать все понятия, связанные с дробями.