Системы уравнений – это системы двух и более уравнений, имеющие более одного неизвестного. Итак, для решения систем мы можем использовать четыре метода: подстановку, уравнение, приведение и графическое представление. Но прежде чем приступить к объяснению процедур решения, определим типы существующих систем в зависимости от количества решений:
- Определенная совместимая система: она имеет только одно решение и может быть представлена двумя прямыми, пересекающимися в одной точке (которая и является решением).
- Неопределенно-совместная система: она имеет бесконечное количество решений, и это связано с тем, что существуют две прямые, совпадающие в одних и тех же точках.
- Несовместная система: она не имеет решения, так как прямые параллельны и, следовательно, не имеют общих точек.
Методы решения систем линейных уравнений
Теперь мы объясним различные системы, которые мы можем использовать для решения систем уравнений. В пояснениях вы найдете теорию и несколько примеров, благодаря которым все излагаемые понятия станут более понятными. Обратите внимание, что в этой статье мы будем говорить только о системах уравнений 2×2 , а это значит, что мы будем иметь дело просто с системами, состоящими из двух уравнений. Тем не менее, давайте начнем с объяснения.
метод замещения
Метод замены заключается в выделении одной из неизвестных в одном из уравнений и последующей подстановке полученного выражения в противоположное уравнение. Этот метод наиболее рекомендуется, когда хотя бы одно из неизвестных имеет значение коэффициента, равное 1. Таким образом, дальнейшие шаги очень просты:
- Выделите неизвестную величину из одного из двух уравнений.
- Подставим в другое уравнение выражение, эквивалентное неизвестному, которое мы исключили из первого уравнения.
- Сотрите противоположное неизвестное в полученном уравнении.
- Как только мы получим значение первой переменной, нам нужно использовать его, чтобы найти вторую.
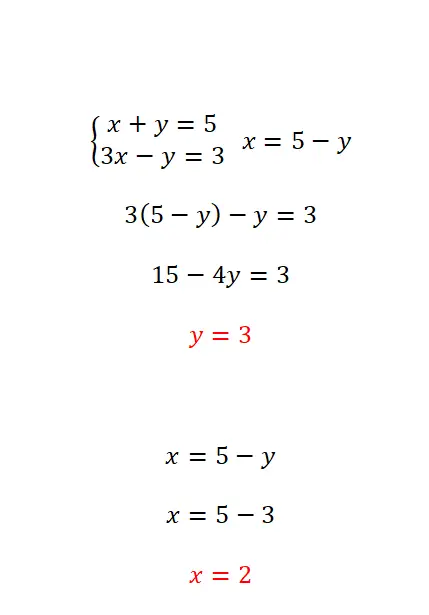
метод выравнивания
Метод сопоставления состоит в выделении одной и той же переменной в двух уравнениях и последующем сопоставлении двух полученных выражений. Этот метод рекомендуется, когда одно и то же неизвестное можно легко выделить в обоих уравнениях, поскольку он упрощает весь расчет. Порядок действий, который необходимо выполнить в этом случае, следующий:
- Мы изолируем неизвестное, которое мы выбрали в двух уравнениях.
- Мы уподобляем этому неизвестному эквивалентные выражения.
- Решаем уравнение обычным способом.
- Мы вычисляем другое неизвестное с помощью рассчитанного нами значения.
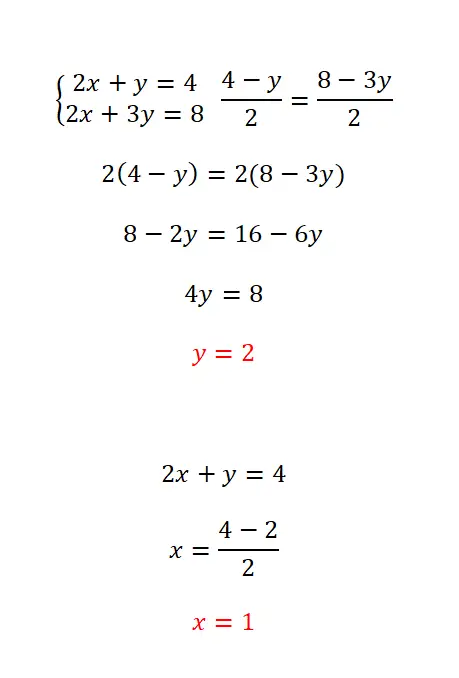
метод сокращения
Метод приведения основан на умножении обоих уравнений на два числа, что позволяет получить один и тот же коэффициент при разном знаке одной из переменных в обоих выражениях. Этот метод наиболее рекомендуется, когда одно и то же неизвестное имеет одинаковый коэффициент во всех уравнениях или в случае наличия одинаковых коэффициентов противоположных знаков. А процедура разрешения следующая:
- Два уравнения умножаются на необходимые числа (нужно найти два числа, которые позволят получить одинаковый коэффициент для одной из двух переменных в двух уравнениях, но противоположного знака).
- Затем уравнения вычитаются или складываются, чтобы исключить это неизвестное с соответствующими коэффициентами.
- Затем решается оставшееся уравнение.
- И мы используем результат этого уравнения, чтобы получить числовое значение, которого нам не хватает в другой переменной.
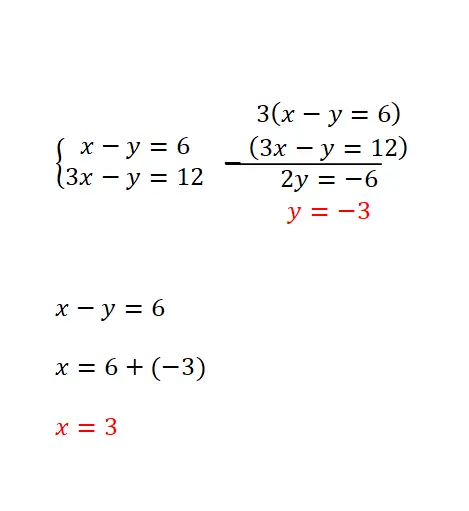
графический метод
Наконец, мы можем решить систему уравнений с помощью графического представления . Этот метод существенно отличается от других, поскольку не имеет сложной математической части, он практически полностью графический. Таким образом, чтобы узнать значения неизвестных, мы должны построить два уравнения в виде уравнения прямой: y = mx + b . Таким образом, мы сможем сделать представление, тогда мы свяжем значения координат точки разреза между двумя функциями с неизвестными. Вот рабочий пример:
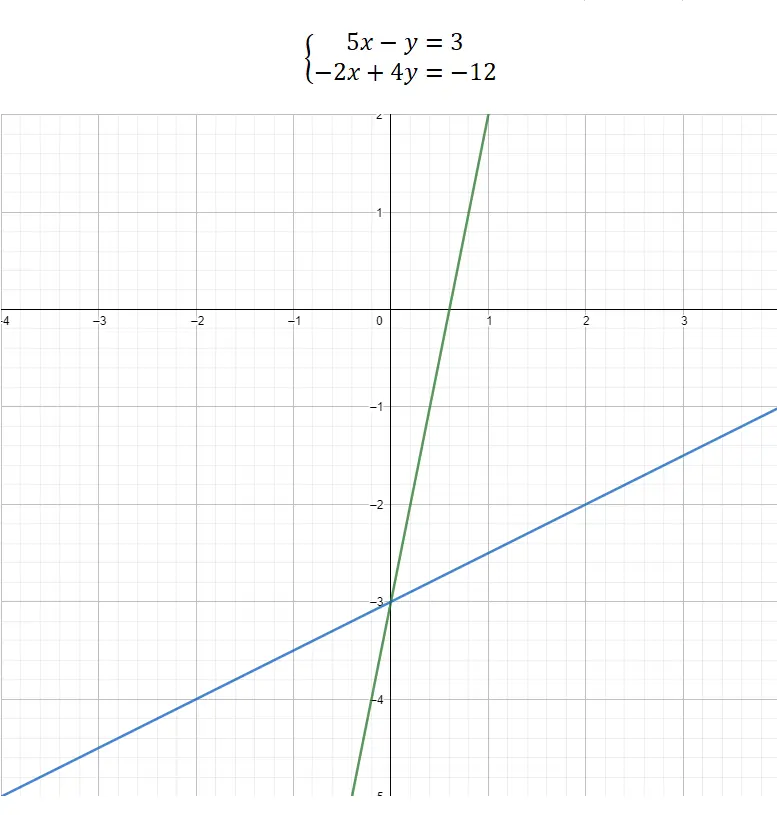
Как видно на графике, точка разделения между двумя функциями равна (0, -3). Следовательно, значение x = 0 и значение y = -3. Вот так графически решается система уравнений.
Как решить систему квадратных уравнений?
Для решения систем квадратных уравнений мы можем использовать методы, которые мы только что обсудили. Лично мы рекомендуем метод замены, поскольку он позволяет быстро получить уравнение с одним неизвестным. С другой стороны, если мы используем методы приведения или уравнения, расчет становится довольно сложным. Итак, как только вы подставите одну из двух переменных, вам останется только решить полученное квадратное уравнение или квадратное уравнение . Вот пример, чтобы вы могли увидеть весь процесс:
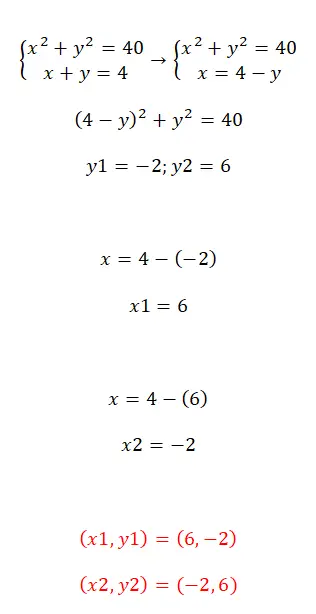
Упражнения по решению систем уравнений
Теперь мы предлагаем вам несколько упражнений на системы линейных и квадратных уравнений, чтобы вы могли применить изложенную теорию. Таким образом, вы лучше поймете все понятия, связанные с расчетом систем уравнений. Мы рекомендуем вам попробовать их решить, прежде чем просматривать предлагаемые нами ответы, так вы получите максимальную пользу от упражнений:
Упражнение 1
Решите данную систему уравнений методом замены:
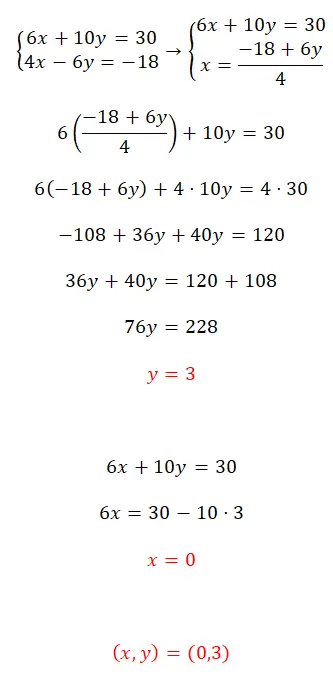
- Начнем с выделения одной из двух неизвестных в уравнении.
- Затем подставим выражение, полученное в противоположном уравнении, на неизвестное, которое мы решили ранее.
- Затем мы получаем результат противоположной переменной.
- Далее мы подставляем первое обнаруженное значение в одно из двух уравнений, чтобы вычислить значение первого неизвестного.
- Наконец, мы выражаем результат двух переменных.
Упражнение 2
Решите данную систему уравнений методом замены:
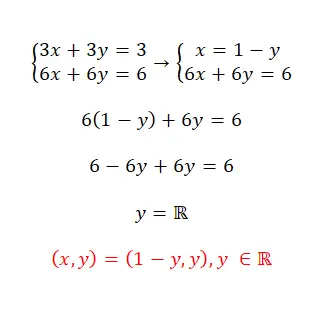
- В этом случае мы поступим той же процедурой: выделим неизвестную, подставим ее в другое выражение и выделим вторую переменную.
- Как мы видим, это неопределенно-совместная система, поскольку она имеет бесконечно много решений.
Упражнение 3
Решите данную систему уравнений методом уравнения:
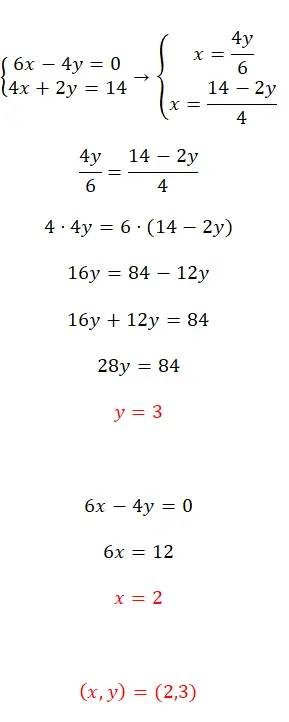
- Первый шаг — выделить одну и ту же переменную в обоих уравнениях, в данном случае мы выбрали x.
- Затем сопоставляем полученные выражения и приступаем к решению.
- Таким образом, мы получаем значение первого неизвестного.
- И если мы подставим его в одно из двух исходных уравнений, мы сможем вычислить второе неизвестное.
- Наконец, мы выражаем результат двух переменных.
Упражнение 4
Решите данную систему уравнений методом уравнения:
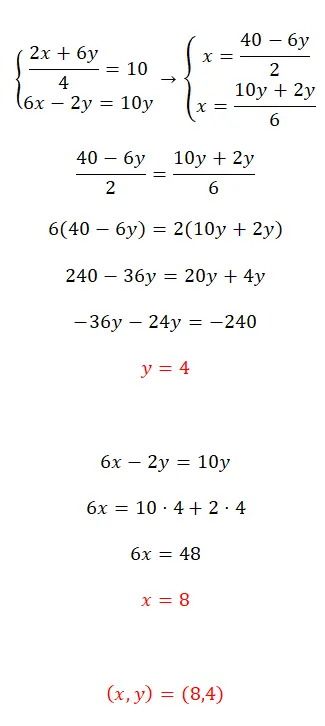
- Сначала мы изолируем x в обоих уравнениях.
- Далее сопоставляем полученные выражения.
- Получаем значение первого неизвестного.
- Подставляем эту величину в одно из двух исходных уравнений и вычисляем второе неизвестное.
- Наконец, мы выражаем ценность двух незнакомцев.
Упражнение 5
Решите данную систему уравнений методом редукции:
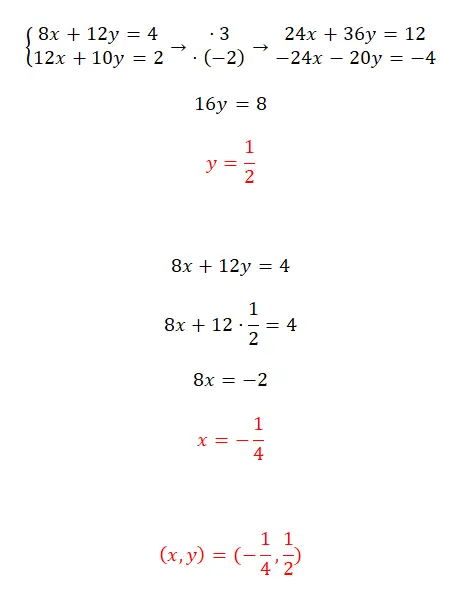
- Вам предстоит искать два числа , позволяющие получить одинаковый коэффициент для одной из двух переменных в двух уравнениях, но противоположного знака .
- Затем просто решим уравнение, которое получим сложением двух полученных выражений.
- Затем мы подставляем y в одно из двух исходных уравнений, чтобы вычислить x.
- Наконец, выражаем результат работы системы.
Упражнение 6
Решите данную систему уравнений методом редукции:
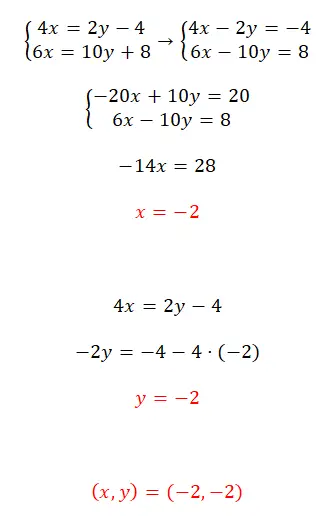
- Начнем с составления уравнений (передавая все переменные слева).
- Затем умножаем первое уравнение на -5.
- Мы решаем уравнение, которое получаем путем сложения двух уравнений, и получаем значение x.
- Мы используем это известное значение, чтобы получить значение y.
- Выразим результат системой уравнений.
Упражнение 7
Решите данную систему уравнений методом замены:
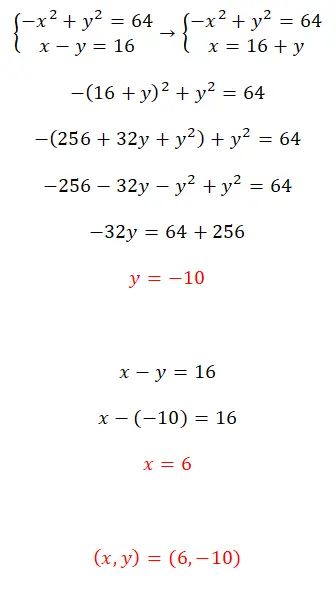
- Для решения данной системы нелинейных уравнений рекомендуем использовать метод замены.
- Итак, вы строите уравнение с выражением, эквивалентным x.
- Вы получаете значение неизвестного y.
- Вы вычисляете значение x с помощью значения, которое вы вычислили ранее.
- И у вас уже есть оба значения.
Упражнение 8
Решите эту систему уравнений, используя метод по вашему выбору:
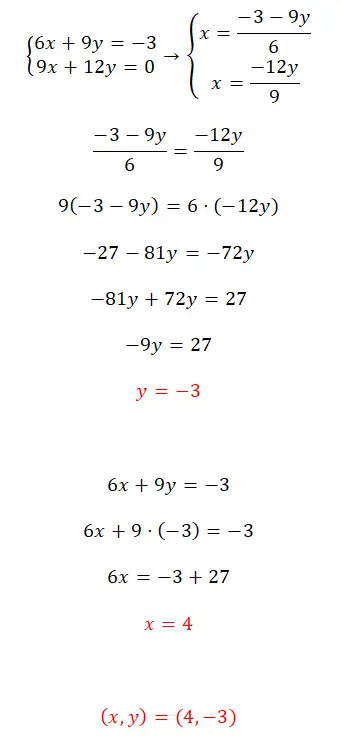
- В данном случае нам представлена определенная совместимая система, и мы будем решать ее методом уравнения.
- Поэтому мы находим x в обоих уравнениях и приравниваем два полученных выражения.
- Решив уравнение, мы получим значение y.
- Мы используем это значение, чтобы найти значение x.
- Наконец, выражаем результат работы системы.