Что такое полиномиальный факторинг? Это математический метод, позволяющий разложить полином на более простые факторы или выражения. И благодаря этому упрощению мы сможем легче и комфортнее выполнять операции между несколькими алгебраическими выражениями. Итак, в этой статье мы обсудим различные методы факторизации полиномов и все возможные случаи факторизации.
Как факторизовать полином?
Существует множество методов факторизации , которые имеют собственную структуру решения, но в конечном итоге полагаются на одно и то же. Кроме того, вы также можете найти множество случаев, касающихся полиномиальной конфигурации. Вот почему в следующих разделах мы обсудим все существующие процедуры и случаи использования каждой из них. Наконец, мы применим это к реальному примеру, чтобы вы завершили усвоение концепций.
Фактор полинома по правилу Руффини
Наиболее используемым методом факторизации многочленов является правило Руффини , поскольку оно просто в использовании и результат можно быстро найти. Обычно этот метод используется для факторизации полиномов степени больше двух или даже иногда для факторизации полиномов второй степени. Так как позволяет очень наглядно получить корни этого многочлена . Хотя это использование будет объяснено в следующем разделе, посвященном корням математического выражения этого типа.
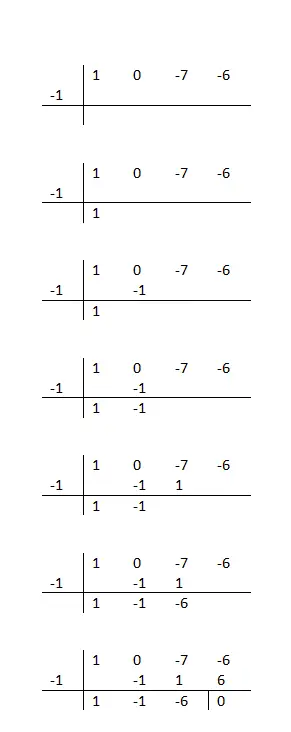
Как заставить Руффини факторизовать полиномы?
По сути, нам придется написать коэффициенты делимого в горизонтальной линии и значение возможного корня многочлена в боковой. Мы говорим «возможно», потому что нам придется искать делитель, который позволит получить остаток, равный нулю. В противном случае это число не будет действительным корнем, и вам придется продолжать попытки.
В качестве совета мы рекомендуем вам пробовать только числа делителей независимого члена (последнее значение горизонтальной линии). Итак, чтобы узнать, правильно ли выбранное вами число, вам достаточно выполнить следующую последовательность вычислений :
Вы уменьшаете коэффициент, умножаете его на проверяемый корень, записываете его под следующим коэффициентом и выполняете вертикальное сложение. Вам просто нужно будет повторить эти шаги до конца, и как только вы закончите, вы узнаете, правильное это значение или нет. Поскольку действительными будут только числа, дающие нулевой остаток.
Если математическая процедура, которой вам нужно следовать, вам не очень понятна, вы можете посмотреть пример в столбце слева от этого текста. Также мы рекомендуем попробовать факторизовать следующий полином: x³ + 2x² – x – 2 (на основе примера). И наконец, чтобы узнать, правильно вы решили упражнение или нет, вы можете сравнить свой результат с этим:
- Избыточное выражение = x² + 3x + 2
- остаток = 0
Теперь мы дадим краткое объяснение применения Руффини в факторизации . Хотя если вы хотите подробно узнать, как используется этот математический ресурс, мы рекомендуем вам обратиться к последней статье, на которую мы ссылались, поскольку там все очень хорошо объяснено. Тем не менее, давайте начнем с объяснения того, как факторизовать полиномы с помощью правила Руффини:
- Рисуем сетку: как видно на изображении выше, мы создадим коробку, в которой сделаем Руффини. По сути, вам нужно записать коэффициенты выражения, упорядоченные по горизонтали, не оставляя тех, которые имеют нулевое значение. В итоге у вас должно получиться представление, похожее на то, что на изображении, но со значениями вашего полинома.
- Вычисляем корни: как только мы нарисовали структуру и убедились, что все числа записаны правильно, приступаем к вычислению корня. Вам нужно будет найти корни, следуя последовательности вычислений, о которой мы говорили чуть выше этого списка (с изображениями).
- Выразим корень в форме (x – a): когда у нас есть все корни многочлена, мы должны выразить их в следующей форме (x – a). Учитывая, что a — полученные нами значения, например, если мы извлекли в результате x = 2, x = -2 и x = 4, то мы получим (x – 2), (x + 2) и ( х – 4).
- Собираем все факторы в одно выражение: наконец, когда у нас уже есть все корни, выраженные в правильном формате, нам остается собрать их в одном алгебраическом выражении. Продолжая предыдущий пример, у нас будет что-то вроде этого: (x – 2) · (x + 2) · (x – 4).
Фактор полинома, используя корни многочлена
Мы наполовину объяснили корневую концепцию многочлена в разделе Руффини. Но точное определение будет таким: корень многочлена P(x) — это числовое значение a, такое что P(a) = 0 . Следовательно, это число, способное отменить рассматриваемую функцию или полином. Подводя итог, можно сказать, что он используется для разложения полинома на произведение факторов.
Например, если нам дано следующее выражение x² − x − 2, и мы факторизуем его либо с помощью правила Руффини, либо просто решая квадратное уравнение x² − x − 2 = 0. Мы получим два значения x = -1 и x = 2, поэтому, если мы изменим их на формат (x – a) и сложим вместе, мы придем к следующему выражению: (x + 1) (x – 2), то есть факторизованному многочлену . И мы можем применить это к многочленам степени больше двух, хотя выражение состоит более чем из одного члена.
Факторизация полинома путем извлечения общего фактора
Если мы хотим факторизовать полиномы без независимого члена или выражения, которые имеют общий фактор во всех терминах, мы можем упростить полином, используя этот метод. По сути, это предполагает применение свойства распределения ко всему выражению, удаление этого повторяющегося общего фактора и добавление его путем умножения всего многочлена. Ниже вы найдете пример первого случая, о котором мы говорили (полином без независимого члена):
2x³ + 10x² – 6x = 2x (x² + 5x – 3)
Двойное выделение общего фактора
Извлечение общего фактора можно даже выполнить путем выделения более сложных факторов, включающих несколько переменных. И вы даже можете извлекать полиномы, полученные из самого основного выражения. Важно не устанавливать ограничений при выполнении операций такого типа, поскольку цель извлечения коэффициентов — максимально упростить алгебраическое выражение .
Факторизация полиномов с использованием заметных тождеств
Известные продукты могут помочь нам факторизовать полиномиальные выражения, поскольку они представляют собой своего рода упрощенные алгебраические выражения. Таким образом, они помогают нам напрямую перейти от длинного полинома к небольшой формуле, состоящей из нескольких членов. Поэтому настоятельно рекомендуется выучить формулы известных личностей, чтобы иметь возможность быстро определить, когда их можно использовать. И, следовательно, мы экономим время на факторинге с помощью Ruffini или любого другого метода. Далее мы рассмотрим три правила, которые вам необходимо усвоить:
- Разность квадратов: a² – b² = (a + b) · (a – b)
- Квадрат суммы: a² + 2ab + b² = (a + b)².
- Квадрат вычитания: a² – 2ab + b² = (a – b)²
Факторизация полиномов путем группировки
В некоторых случаях мы можем найти многочлен структуры x² – ax – bx + ab , который можно упростить, удалив общий множитель: x (x – a) – b (x – a). А если снова взять общий делитель, то его можно еще упростить: (x – a) · (x – b). Следовательно, корнями этого многочлена будут x = a и x = b. Как видите, этот тип алгебраического выражения имеет структуру, которую очень легко разложить и использовать.
Упражнения по полиномиальной факторизации
Наконец, мы хотим предложить вам серию упражнений , чтобы вы могли попрактиковаться в факторизации полиномов. Таким образом, вы сможете лучше усвоить теорию, которую мы объяснили сегодня. Проще говоря, вы должны решить упражнения в тетради, а затем сравнить результаты с теми, которые мы предлагаем вам ниже.
- х 4 -1 = (х 2 + 1) (х + 1) (х – 1)
- х 5 + х 4 – х – 1 = (х – 1) (х + 1) 2 (х 2 + 1)
- 9х2 + 30х + 25 = (3х + 5) 2
- х 4 – 3х 3 – 3х 2 + 11х – 6 = (х + 2) (х – 3) (х – 1) 2