▷ Что это такое и как представить квадратичную функцию (или параболу)

На этой странице объясняется, что такое квадратичная функция, а также все ее характеристики: кривизна, вершина, точки пересечения с осями и т. д. Вы также научитесь представлять квадратичную функцию на графике. И, наконец, вы можете попрактиковаться на примерах, пошаговых упражнениях и задачах на квадратичные функции.

Что такое квадратичная функция?

Определение квадратичной функции выглядит следующим образом:

В математике квадратичная (или параболическая) функция — это полиномиальная функция второй степени, то есть функция, в которой старший член имеет вторую степень. Следовательно, формула квадратичной функции имеет вид:

$f(x)=ax^2+bx+c$

Золото:

$ax^2$

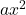
является квадратичным членом.
$bx$

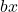
является линейным членом.
$c$

является независимым термином.

Область определения квадратичной функции всегда состоит из действительных чисел.

$\text{Dom } f=\mathbff{R}$

Вогнутость и выпуклость квадратичной функции

Анализировать кривизну квадратичной или параболической функции очень просто, поскольку она зависит только от квадратичного коэффициента.

Если коэффициент
$a$

положительна, квадратичная функция выпукла (в виде

$\bm{\cup}$

). Поэтому саммит – это минимум.
Если коэффициент
$a$

отрицательна, квадратичная функция вогнута (имеет форму

$\bm{\cap}$

). Таким образом, пик является максимумом.

квадратичная функция или выпуклая парабола

квадратичная функция или вогнутая парабола

Примечание. Математическое сообщество до сих пор не до конца согласны и поэтому некоторые профессора говорят обратное: они называют вогнутой функцию, имеющую форму

$\bm{\cup}$

и выпуклая функция, имеющая вид

$\bm{\cap}$

. В любом случае важно то, какую форму имеет функция, какое бы название она ни имела.

Вершина квадратичной функции

Чтобы построить график квадратичной функции, необходимо знать координаты вершины параболы.

Чтобы найти вершину квадратичной функции, нам нужно вычислить координату X точки по следующей формуле:

$\displaystyle x=\frac{-b}{2a}$

Затем мы можем найти координату другой вершины, вычислив образ функции в этой точке:

$\displaystyle f\left(\frac{-b}{2a}\right)$

Таким образом, координаты вершины квадратичной функции (или параболы):

$\displaystyle \left(\frac{-b}{2a} \ , \ f\left(\frac{-b}{2a}\right)\right)$

Точки разрезания осями квадратичной функции

Парабола всегда пересекает ось Y (ось Y), и это происходит, когда

$x=0.$

Следовательно, чтобы вычислить точку отсечки квадратичной функции с осью Y, необходимо решить

$f(0).$

Например, точка пересечения с осью OY следующей квадратичной функции:

$f(x)=x^2-2x+1$

$f(0)=0^2-2\cdot 0+1 = 1$

$\bm{(0,1)}$

С другой стороны, точка отсечки квадратичной функции с осью X (ось X) возникает, когда

$f(x)=0.$

Итак, чтобы вычислить точку пересечения с осью X, вам нужно решить уравнение

$f(x)=0.$

В качестве примера ниже приведен расчет точки отсечки по оси OX той же квадратичной функции:

$f(x)=x^2-2x+1$

$0=x^2-2x+1$

Решаем квадратное уравнение по общей формуле:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\cfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot1}}{2\cdot 1} =\cfrac{2\pm 0}{2} = 1$

Таким образом, точка пересечения квадратичной функции с осью X равна:

$\bm{(1,0)}$

В этом случае мы получили только одно решение квадратного уравнения, но могли бы получить и два решения. В данном случае это означает, что квадратичная функция пересекает ось X в двух разных точках.

Пример представления квадратичной или параболической функции

Давайте посмотрим, как изобразить квадратичную функцию на графике на примере.

Постройте график следующей функции:

$f(x)=x^2-4x+5$

Первое, что нужно сделать, это вычислить вершину параболы. Для этого воспользуемся формулой, которую мы видели выше:

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2$

Как только мы узнаем, где будет вершина, нам нужно построить таблицу значений: Вычисляем значение функции в вершине и в окружающих ее точках:

$f(x)=x^2-4x+5$

$x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot2+5=1$

$x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot1+5=2$

$x= 3 \ \longrightarrow \ f(3) = 3^2-4\cdot3+5=2$

$x= 0 \ \longrightarrow \ f(0) = 0^2-4\cdot0+5=5$

$x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot4+5=5$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 1 \\ 1 & 2 \\ 3 & 2 \\ 0 & 5 \\ 4 & 5 \end{array}$

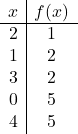
Вы также можете вычислить точки разреза квадратичной функции с помощью декартовых осей, чтобы лучше нарисовать параболу, но это не является строго необходимым.

Теперь представим полученные точки на графике :

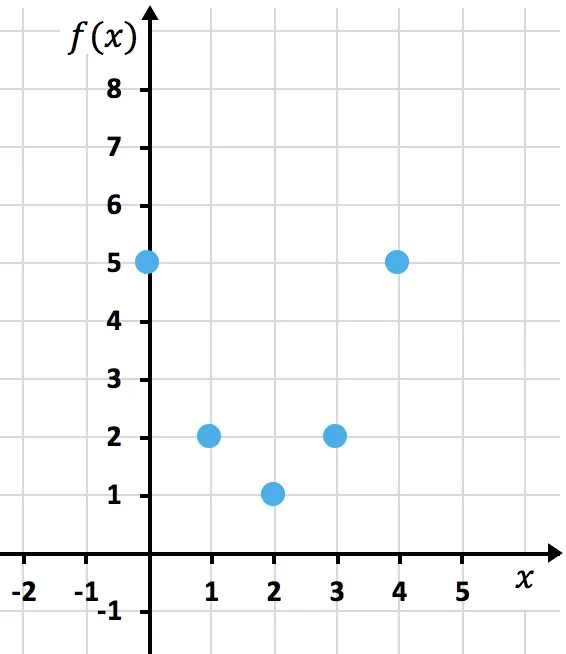
пример того, как представить квадратичную или параболическую функцию

И, наконец, соединяем точки, образующие параболу. Затем мы удлиняем ветви параболы, чтобы указать, что она продолжается вверх:

представление квадратичной или параболической функции

Решенные упражнения на квадратичные функции

Упражнение 1

Найдите вершину следующей квадратичной функции:

$f(x)=2x^2+8x+4$

Посмотреть решение

Сначала вычисляем координату X вершины по формуле:

$x = \cfrac{-b}{2a} = \cfrac{-8}{2\cdot 2} = \cfrac{-8}{4} = -2$

И теперь мы вычисляем другую координату, оценивая функцию в точке:

$\begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}$

Следовательно, вершина квадратичной функции равна:

$\bm{(-2,-4)}$

Упражнение 2

Найдите точки среза следующей функции с осями:

$f(x)=x^2-4x+3$

Посмотреть решение

Чтобы рассчитать точку разреза по оси Y, нам нужно вычислить

$f(0):$

$f(0)=0^2-4\cdot 0+3 = 3$

Таким образом, функция проходит через ось Y в точке:

$\bm{(0,3)}$

И чтобы найти точки разреза по оси X нам нужно решить

$f(x)=0:$

$f(x)=x^2-4x+3$

$0=x^2-4x+3$

Вычисляем корни квадратного уравнения по формуле:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}$

Таким образом, функция разрезает ось X в двух точках:

$\bm{(1,0) \qquad (3,0)}$

Упражнение 3

Постройте график следующей квадратичной функции:

$f(x)=-x^2+4x+1$

Посмотреть решение

Это квадратичная функция. следовательно, чтобы его представить, необходимо сначала вычислить абсциссу вершины параболы по формуле:

$x = \cfrac{-b}{2a} = \cfrac{-4}{2\cdot (-1)} = \cfrac{-4}{-2} = 2$

Теперь создаем таблицу значений. Для этого рассчитаем стоимость

$f(x)$

вверху и вокруг верха:

$x= 2 \ \longrightarrow \ f(2)=-2^2+4\cdot2+1 = 5$

$x= 1 \ \longrightarrow \ f(1)=-1^2+4\cdot1+1 = 4$

$x= 3 \ \longrightarrow \ f(3)=-3^2+4\cdot3+1 =4$

$x= 0 \ \longrightarrow \ f(0)=-0^2+4\cdot0+1 = 1$

$x= 4 \ \longrightarrow \ f(4)=-4^2+4\cdot4+1 = 1$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 5 \\ 1 & 4 \\ 3 & 4 \\ 0 & 1 \\ 4 & 1 \end{array}$

И наконец, наносим точки на график и рисуем параболу:

Упражнение 4

Постройте график следующей квадратичной функции:

$f(x)=-2x^2-8x-1$

Посмотреть решение

Это функция второго порядка. следовательно, чтобы ее представить, необходимо сначала найти абсциссу вершины параболы по формуле:

$x = \cfrac{-b}{2a} = \cfrac{-(-8)}{2\cdot (-2)} = \cfrac{+8}{-4} = -2$

Теперь строим таблицу значений. Для этого рассчитаем стоимость

$f(x)$

вверху и вокруг верха:

$x= -2 \ \longrightarrow \ f(-2)=-2(-2)^2-8\cdot(-2)-1 =7$

$x= -1 \ \longrightarrow \ f(-1)=-2(-1)^2-8\cdot(-1)-1= 5$

$x= -3 \ \longrightarrow \ f(-3)=-2(-3)^2-8\cdot(-3)-1= 5$

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0^2-8\cdot0-1= -1$

$x= -4 \ \longrightarrow \ f(-4)=-2(-4)^2-8\cdot(-4)-1= -1$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 7 \\ -1 & 5 \\ -3 & 5 \\ 0 & -1 \\ -4 & -1 \end{array}$

Наконец, наносим точки на график и рисуем параболу:

Упражнение решено шаг за шагом квадратичной функции

Упражнение 5

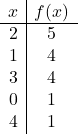
Постройте на графике следующую неполную квадратичную функцию:

$f(x)=x^2+2$

Посмотреть решение

Это полиномиальная функция второй степени. следовательно, чтобы его представить, необходимо сначала вычислить абсциссу вершины параболы по формуле:

$x = \cfrac{-b}{2a} = \cfrac{-0}{2\cdot1} = \cfrac{0}{2} = 0$

В этом случае функция является неполной, так как не имеет члена первой степени. Для этого

$b=0 .$

Теперь составляем таблицу значений. Для этого рассчитаем стоимость

$f(x)$

вверху и вокруг верха:

$x= 0 \ \longrightarrow \ f(0)=0^2+2=2$

$x= 1 \ \longrightarrow \ f(1)=1^2+2=3$

$x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2=3$

$x= 2 \ \longrightarrow \ f(2)=2^2+2=6$

$x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2=6$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ -1 & 3 \\ 2 & 6 \\ -2 & 6 \end{array}$

Наконец, наносим точки на график и рисуем параболу:

решены упражнения на представление неполной квадратичной функции

Упражнение 6

Решите следующую задачу, связанную с квадратичными функциями:

Стоимость производства продукции определяется следующей функцией:

$f(x)=x^2-12x+76$

Золото

$x$

произведено единиц продукции (в тысячах) и

$f(x)$

— себестоимость единицы продукции (в тысячах евро).

Представляет функцию производственных затрат на графике.
Определите, сколько тысяч единиц продукции следует произвести, чтобы минимизировать затраты.

Посмотреть решение

Это квадратичная функция. следовательно, чтобы ее представить, необходимо сначала найти абсциссу вершины параболы по формуле:

$x = \cfrac{-b}{2a} = \cfrac{-(-12)}{2\cdot 1} = \cfrac{12}{2} = 6$

Теперь составляем таблицу значений. Для этого рассчитаем стоимость

$f(x)$

вверху и вокруг верха:

$x= 6 \ \longrightarrow \ f(6)=6^2-12\cdot6+76 = 40$

$x= 5 \ \longrightarrow \ f(5)=5^2-12\cdot5+76 = 41$

$x= 7 \ \longrightarrow \ f(7)=7^2-12\cdot7+76 = 41$

$x= 4 \ \longrightarrow \ f(4)=4^2-12\cdot4+76 = 44$

$x= 8 \ \longrightarrow \ f(8)=8^2-12\cdot8+76 = 44$

$\begin{array}{c|c} x & f(x) \\ \hline 6 & 40 \\ 5 & 41 \\ 7 & 41 \\ 4 & 44 \\ 8 & 44 \end{array}$

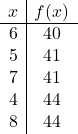
Теперь наносим точки на график и рисуем параболу:

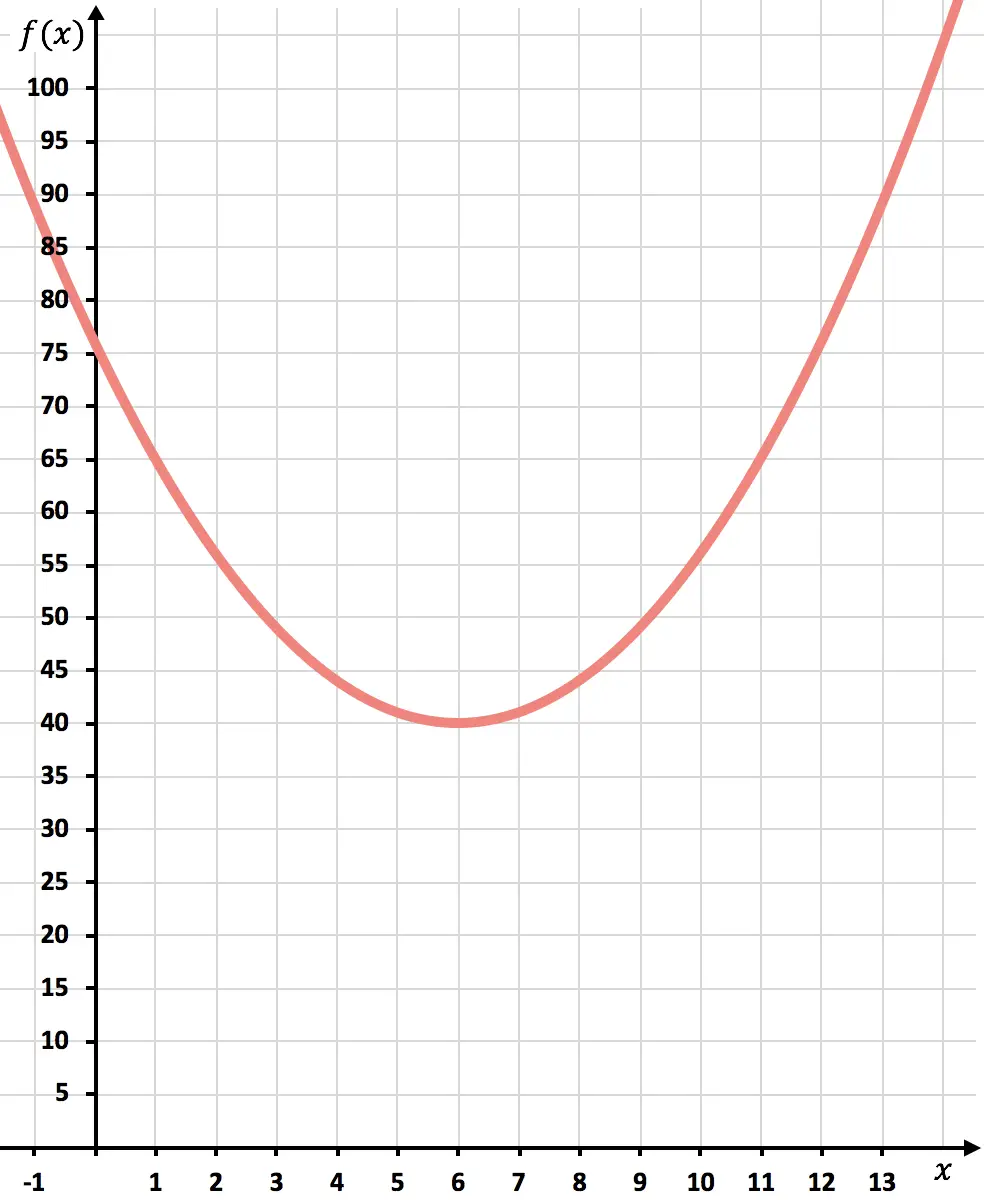
задача о квадратичной или параболической функции

Как только функция будет представлена, мы увидим, насколько минимизируются затраты.

Как видно из графика, минимальные затраты будут достигнуты на вершине параболы. Потому что именно здесь функция принимает наименьшее значение.

В заключение, затраты будут минимизированы за счет производства 6000 единиц.

Упражнение 7

Решите следующую задачу о квадратичной функции:

Спортсмен выполняет метание копья, траекторию которого можно представить следующей функцией:

$h(x) = -0,025x^2+2x+2$

Золото

$x$

метры, пройденные копьем и

$h$

его высота (тоже в метрах).

Какую максимальную высоту может достичь копье?

Посмотреть решение

Это квадратичная функция, поэтому траектория копья будет параболой.

Кроме того, поскольку коэффициент при квадратичном члене отрицательный (-0,025), парабола будет иметь форму перевернутой буквы U и ее ветви будут идти вниз. Таким образом копье достигнет максимальной высоты вверху, так как это будет самая высокая точка параболы.

Поэтому мы вычисляем абсциссу вершины параболы по формуле:

$x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot (-0,025)} = \cfrac{-2}{-0,05} = 40$

А затем мы вычисляем, насколько высоко будет находиться копье в этот момент, оценивая функцию в

$x=40:$

$h(40) = -0,025\cdot (40)^2+2\cdot 40+2 = 42$

Таким образом, максимальная высота, которую может достичь копье, составляет 42 метра.

Упражнение 8

Решите следующую задачу относительно квадратичных функций:

Производственные затраты (в евро) компании определяются следующей функцией:

$C(q)=40000+20q+q^2$

Золото

$q$

произведено единиц продукции.

Цена продажи каждой единицы составляет 520 евро.

Какую прибыль получит компания, если продаст 150 единиц продукции?
Сколько единиц следует продать, чтобы получить максимальную прибыль?

Посмотреть решение

Компания зарабатывает 520 евро за каждую проданную единицу продукции. Следовательно, функция, определяющая доход:

$I(q)=520\cdot q = 520q$

Золото

$q$

продано единиц.

Но нас спрашивают о прибыли, то есть о доходах минус затраты. Поэтому мы вычитаем выручку минус затраты, чтобы получить функцию, описывающую прибыль компании:

$B(q)=I(q)-C(q)$

$B(q)=520q - (40000+20q+q^2)$

$B(q)=520q - 40000-20q-q^2$

$B(q)=-q^2 + 500q - 40000$

Как только мы узнаем функцию, описывающую прибыль компании, просто подставьте 150 в выражение функции, чтобы рассчитать прибыль, которую компания получит от продажи 150 единиц:

$\begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}$

Таким образом, продав 150 единиц, компания получит прибыль в размере 12 500 евро.

В заявлении также содержится просьба подсчитать, на скольких единицах достигается максимальная прибыль.

Функция, описывающая прибыль, является квадратичной функцией, поэтому она будет иметь форму параболы. А так как коэффициент при квадратичном члене отрицательный (-1), то парабола будет иметь форму перевернутой буквы U и ее ветви будут идти вниз. Поэтому максимальный выигрыш будет достигнут вверху, так как это высшая точка параболы.

Поэтому мы вычисляем абсциссу вершины параболы по формуле:

$x = \cfrac{-b}{2a} = \cfrac{-500}{2\cdot(-1)} = \cfrac{-500}{-2} = 250$

Таким образом, компания получит максимальную прибыль, продав 250 единиц.

С другой стороны, даже если об этом не говорится в пресс-релизе, мы можем определить прибыль, которую получим от продажи этих 250 единиц:

$B(250) =-(250)^2 + 500\cdot250- 40000= 22500$

€

Квадратичная функция или парабола

Что такое квадратичная функция?

Вогнутость и выпуклость квадратичной функции

Вершина квадратичной функции

Точки разрезания осями квадратичной функции

Пример представления квадратичной или параболической функции

Решенные упражнения на квадратичные функции

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Упражнение 6

Упражнение 7

Упражнение 8

Оставьте комментарий Отменить ответ