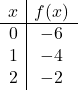На этой странице объясняется, что такое функция абсолютного значения. Вы также узнаете, как определить кусочную функцию абсолютного значения и как представить эти типы функций на графике. Кроме того, вы увидите это на примерах функций абсолютных значений и сможете попрактиковаться, выполняя упражнения и решая задачи шаг за шагом.
Что такое абсолютнозначные функции?
Определение функции абсолютного значения следующее:
Абсолютное значение функции превращает все ее образы в положительные образы. Следовательно, путь абсолютной функции никогда не может иметь отрицательные значения.
Следующая функция является примером функции абсолютного значения:
![]()
Если при вычислении функции в точке получен положительный результат, он остается положительным:
![]()
С другой стороны, если результат отрицательный, он становится положительным:
![]()
Функции абсолютного значения обычно изучают в старших классах школы, поскольку их характеристики затрудняют понимание.
Как кусочно определить функцию с абсолютным значением
Абсолютную функцию можно выразить как кусочную функцию. Для этого необходимо изменить знак функции на интервалах, который становится отрицательным.
Давайте посмотрим пример того, как перейти от функции абсолютного значения к кусочной функции:
- Выразите следующую функцию с абсолютным значением как кусочную функцию:
![]()
Первое, что нам нужно сделать, это определить, когда функция отрицательна. Для этого присвоим алгебраическому выражению по модулю равную 0 и решим уравнение:
![]()
![]()
![]()
![]()
![]()
Теперь представляем полученные значения в строке:
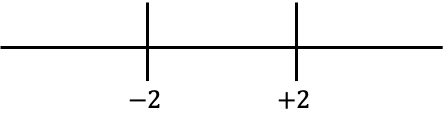
И смотрим, какой знак имеет функция без абсолютного значения в каждом интервале строки:
![]()
Возьмем любую точку меньше -2, например
![]()
![]()
![]()
Отрицательный
![]()
Возьмем любую точку между -2 и +2, например
![]()
![]()
![]()
Позитивный
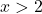
![]()
![]()
![]()
Отрицательный

Как мы видели, функция без абсолютного значения была бы отрицательной на интервалах
![]()
И

![\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -(4-x^2) & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -(4-x^2) & \text{si} & x>2 \end{array} \right.» title=»Rendered by QuickLaTeX.com» height=»97″ width=»372″ style=»vertical-align: 0px;»></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5f441ea5792fb5cc7ba8300f71defef_l3.png)
![\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -4+x^2 & \text{si} & x>2 \end{array} \right.» title=»Rendered by QuickLaTeX.com» height=»97″ width=»358″ style=»vertical-align: 0px;»></p>
</p>
<p> Обратите внимание, что в некоторых интервалах необходимо включать равенство. Например, здесь мы помещаем его во второй интервал</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-89ab8a514afe36c94d7072efe47ef507_l3.png)
![]()
. Но вы можете поместить его в любой интервал, который вам нужен, при условии, что во всех критических точках существует равенство. Другими словами, было бы то же самое, если бы мы определили функцию следующим образом:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-5cce3bcc22edb3a7f511cea0a1c32372_l3.png)
Как представить функцию с абсолютным значением
Чтобы представить функцию с абсолютным значением на графике, нам необходимо выполнить шаги, описанные ниже:
- Представьте функцию так, как если бы она не имела абсолютного значения.
- В промежутках, в которых функция отрицательна, то есть лежит ниже оси X, нарисуйте симметричную функцию.
- Удалите часть функции, которая находится ниже оси X.
Давайте посмотрим пример того, как построить график функции с абсолютным значением.
- Постройте график следующей функции в абсолютном значении:
![]()
Чтобы представить функцию с абсолютным значением, мы должны сначала представить функцию без абсолютного значения. Поэтому составляем таблицу значений функции без абсолютного значения:
![]()
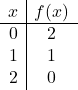
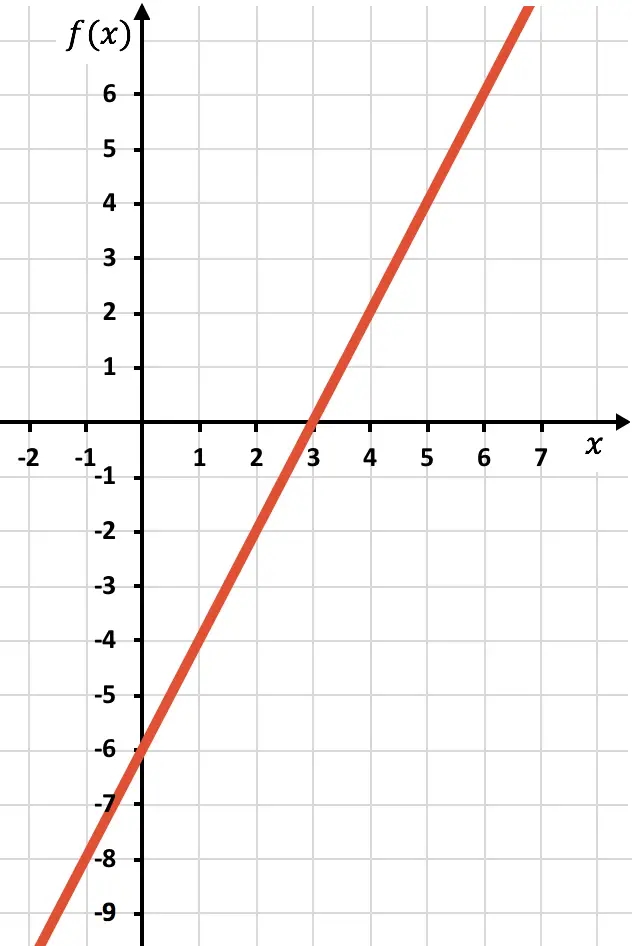
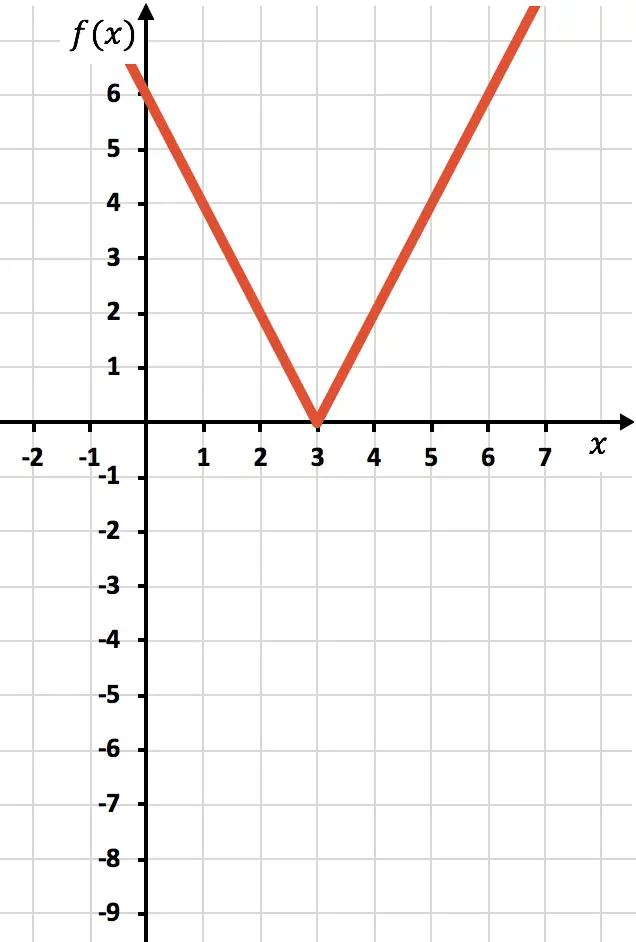
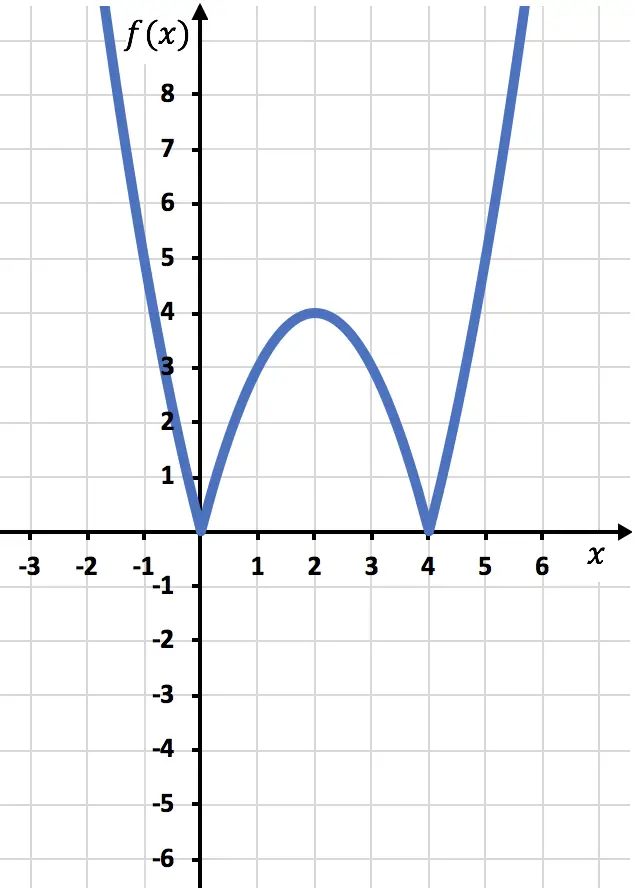
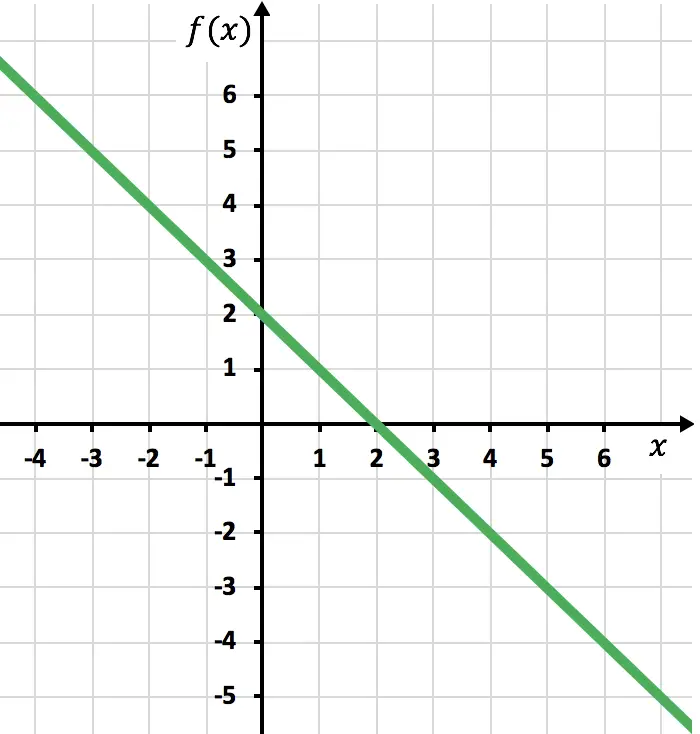
Мы наносим точки на график и рисуем линию, как если бы это была обычная функция:
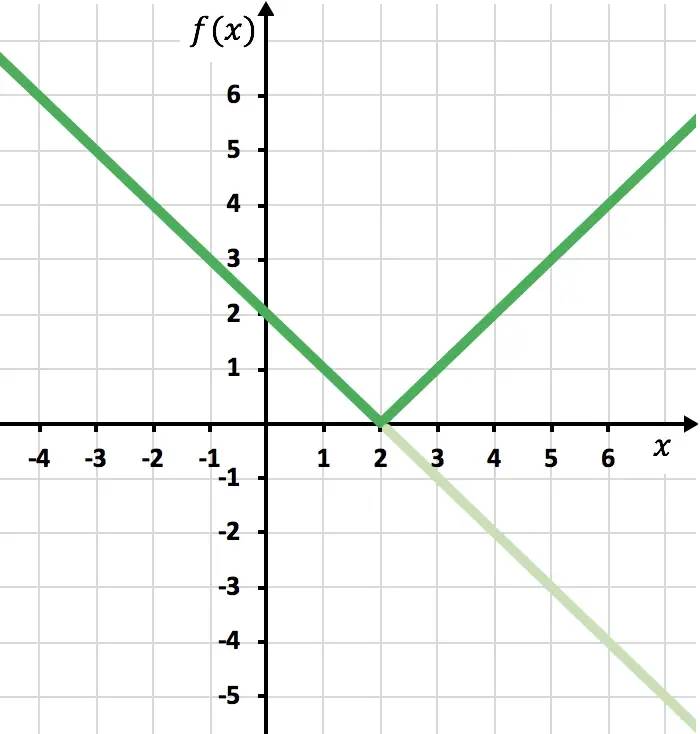
Теперь нам нужно нарисовать симметричную функцию там, где функция отрицательна, то есть там, где она лежит ниже оси x. Поэтому мы обращаем функцию, начиная с x=2:
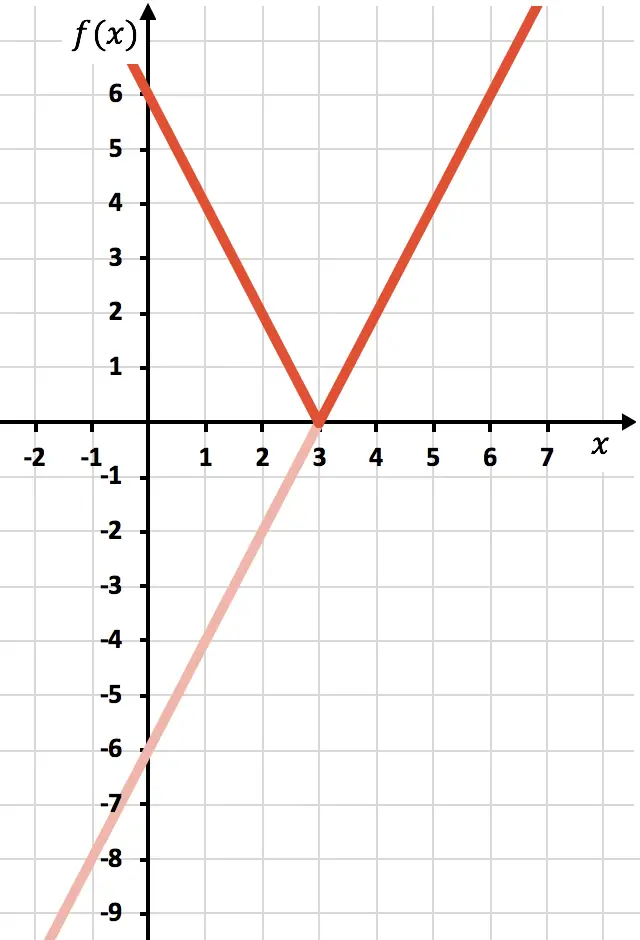
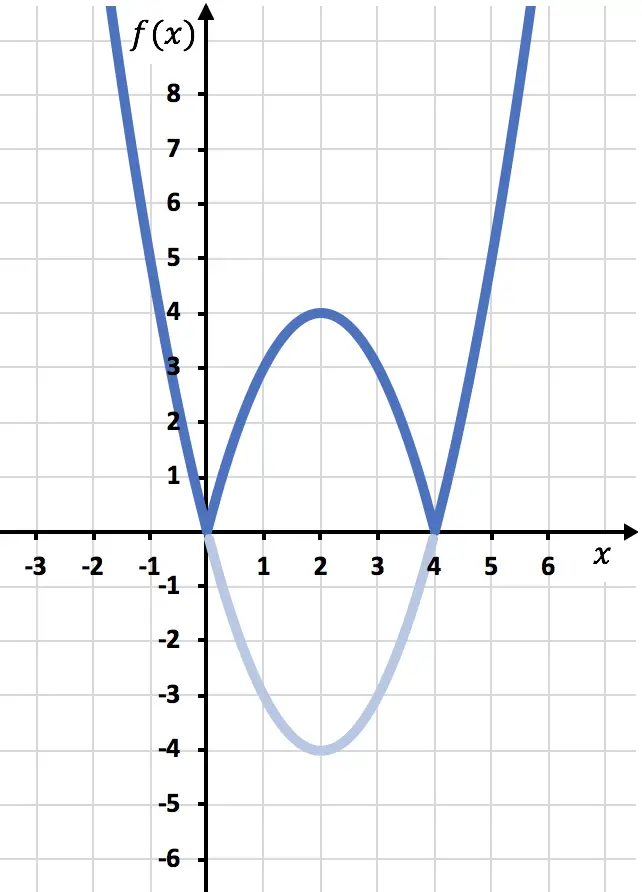
И, наконец, устраняем след функции, расположенный ниже оси X:

Таким образом, мы уже представили функцию с абсолютным значением. Как вы видели, единственное, что меняется, это то, что мы должны инвертировать ту часть функции, которая расположена ниже оси OX. Следовательно, график любой функции с абсолютным значением всегда будет лежать на стороне положительной полуоси Y.
С другой стороны, если рассматривать концепции, из графика мы можем сделать вывод, что область определения предыдущей функции абсолютного значения полностью состоит из действительных чисел. С другой стороны, диапазон или диапазон указанной функции с абсолютным значением состоит только из положительных чисел и нулей.
Решенные упражнения на функции абсолютного значения
Упражнение 1
Выразите следующую функцию с абсолютным значением как кусочную функцию:
![]()
Прежде всего, нам нужно посмотреть, когда функция отрицательна. Для этого приравняем абсолютное значение нулю и решим уравнение:
![]()
![]()
Представляем найденное значение в строке:
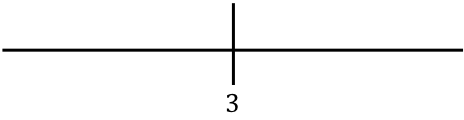
Теперь оцениваем точку в каждом интервале функции без абсолютного значения, чтобы узнать, какой знак на самом деле имеет функция на каждом участке линии:
![]()
Например, возьмем любую точку меньше 3
![]()
![]()
![]()
Позитивный
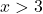 Например, возьмем любую точку больше 3
Например, возьмем любую точку больше 3
![]()
![]()
![]()
Отрицательный
Функция без абсолютного значения будет отрицательной в интервале x>3. Поэтому мы должны выразить функцию тире, изменив ее знак на этом интервале:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7cfaaff9890b356f1db6805ed94dbb8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d249715b500ad03c44ab6ab5838e32e8_l3.png)
Упражнение 2
Найдите кусочное выражение следующей функции с абсолютным значением:
![]()
Первое, что нам нужно сделать, это определить, когда функция отрицательна. Для этого нам нужно установить аргумент абсолютного значения равным нулю и решить уравнение:
![]()
![]()
![]()
![]()
![]()
Теперь представим корни полученной справа функции:
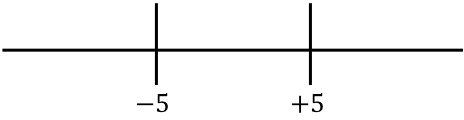
И смотрим, какой знак имеет функция без абсолютного значения в каждом интервале строки:
![]()
Например, возьмем любую точку меньше -5.
![]()
![]()
![]()
![]()
Позитивный
![]()
Возьмем любую точку между -5 и +5, например
![]()
![]()
![]()
![]()
Отрицательный
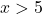 Например, возьмем любую точку больше 5
Например, возьмем любую точку больше 5
![]()
![]()
![]()
![]()
Позитивный

Следовательно, функция без абсолютного значения будет отрицательной только в интервале -5<x<5. Поэтому нам нужно выразить функцию в частях, изменив только знак этого интервала:
![\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.» title=»Rendered by QuickLaTeX.com» height=»97″ width=»408″ style=»vertical-align: 0px;»></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e0fad2e3a9e1a6d1edcde507e60230b_l3.png)
![\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -3x^2+75 & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.» title=»Rendered by QuickLaTeX.com» height=»97″ width=»394″ style=»vertical-align: 0px;»></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f9638fe87ad09d7dbcdb8e30a16688f_l3.png)