Здесь вы узнаете, как рассчитывается расстояние от линии до плоскости, а также сможете увидеть примеры и пошагово решаемые упражнения.
Каково расстояние между прямой и плоскостью?
В аналитической геометрии расстояние между линией и плоскостью в пространстве зависит от относительного положения между этими двумя геометрическими элементами:
- Если линия включена в плоскость или если линия и плоскость параллельны , расстояние, разделяющее их, равно нулю.
- Если линия параллельна плоскости , расстояние от линии до плоскости можно найти, взяв любую точку на линии и вычислив расстояние от этой точки до плоскости.
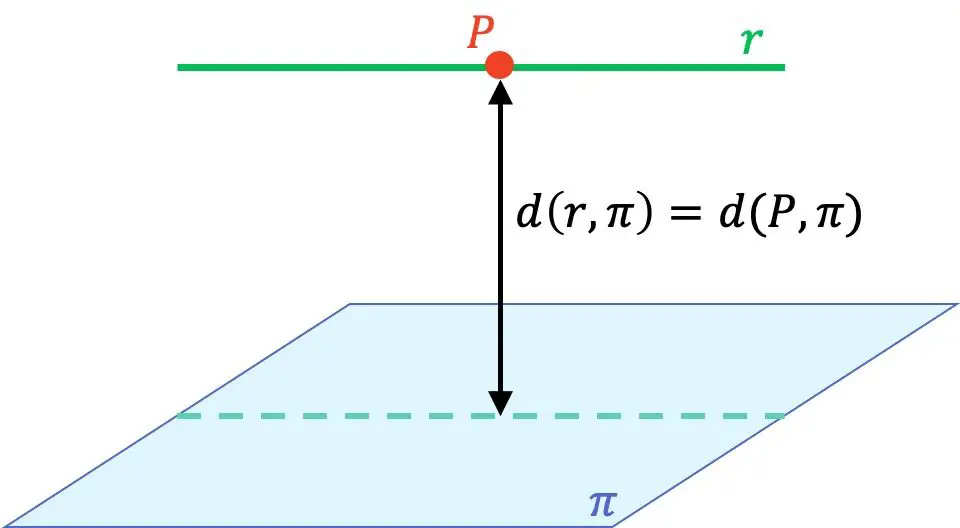
Поэтому для расчета расстояния от линии до плоскости важно знать, как определить относительное положение между линией и плоскостью и как рассчитать расстояние между точкой и плоскостью . Поэтому, если вам не совсем понятно или вы не знаете формулы, рекомендуем сначала просмотреть связанные страницы, где вы найдете пошаговые пояснения, примеры и решенные упражнения.
Пример расчета расстояния между линией и плоскостью
Чтобы вы увидели, как найти расстояние между прямой и плоскостью в пространстве (в R3), на примере решим задачу:
- Как далеко находится линия

на самолете
?
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4785f2386b4ff9387b56cf8c5645c62d_l3.png)
![]()
Чтобы найти расстояние между линией и плоскостью, вы должны сначала знать относительное положение между ними.
С одной стороны, линия задается в виде параметрических уравнений, поэтому ее вектор направления и точка, через которую она проходит, равны:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0765b71f9eead3b644fd5de150cdf321_l3.png)
И, с другой стороны, вектор нормали к плоскости:
![]()
Таким образом, чтобы определить взаимное положение плоскости и линии, необходимо вычислить скалярное произведение вектора направления линии и вектора нормали к плоскости:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39d2d450c32a6fdf3182a3d16cc18116_l3.png)
Результат скалярного произведения равен нулю, поэтому линия может находиться только в плоскости или быть параллельной ей. Итак, чтобы выяснить, какой это случай, подставим декартовы координаты точки на прямой в уравнение плоскости:
![]()
![]()
![]()
Подставляя точку прямой в уравнение плоскости, мы получаем неравенство, следовательно, точка не подчиняется уравнению плоскости и, следовательно, прямая и плоскость параллельны.
Зная, что линия и плоскость параллельны, мы можем вычислить геометрическое расстояние между ними. Для этого мы берем точку на прямой и вычисляем расстояние от этой точки до плоскости.
![]()
Итак, воспользуемся формулой расстояния от точки до плоскости:
![]()
Теперь подставим значение каждого неизвестного в формулу:
![]()
И, наконец, выполняем операции:
![]()
![]()
![]()
Чтобы расстояние между линией и плоскостью было эквивалентно расстоянию между точкой и плоскостью, рассчитанному:
![]()
Очевидно, что расстояние всегда должно давать нам положительное значение, потому что расстояния всегда положительны. Если мы получим отрицательный результат, значит, мы допустили ошибку при совершении шага.