▷ Как вычислить середину отрезка? (формула)

На этой странице объясняется значение средней точки сегмента. Кроме того, вы узнаете, как найти середину отрезка по его формуле. Вы даже увидите примеры, упражнения и решенные задачи о средних точках сегментов.

Что такое середина отрезка?

В математике серединой отрезка называется точка, расположенная на одинаковом расстоянии от концов отрезка. Таким образом, середина делит сегмент на две равные части.

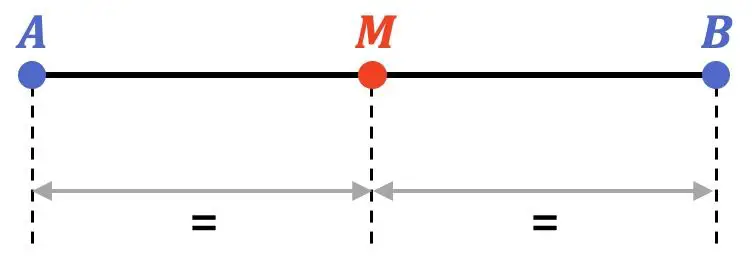
Кроме того, средняя точка находится прямо в центре сегмента, поэтому она принадлежит биссектрисе сегмента.

С другой стороны, середина отрезка также является точкой, равноудаленной от двух геометрических элементов: двух концов отрезка.

Как вычислить середину отрезка?

Учитывая декартовы координаты крайних точек отрезка:

$A(x_1,y_1) \qquad B(x_2,y_2)$

Координаты середины указанного отрезка соответствуют полусумме координат крайних точек:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

Это формула середины отрезка в декартовой плоскости (в R2). Но очевидно, что формула применима и к декартову пространству (в R3), вам просто нужно добавить полусумму координаты Z:

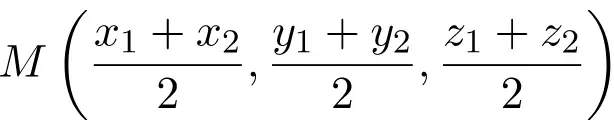
Давайте рассмотрим пример, как вычислить координаты середины отрезка:

Определите середину отрезка, образованного следующими точками:

$A(2,5) \qquad B(4,-1)$

Чтобы найти середину отрезка, просто примените его формулу:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{2+4}{2} , \frac{5+(-1)}{2} \right)$

$\displaystyle M\left(\frac{6}{2} , \frac{4}{2} \right)$

$\displaystyle \bm{M\left(3,2\right)}$

Упражнения решаются в середине сегмента.

Упражнение 1

Какова середина отрезка, конечными точками которого являются следующие две точки?

$A(3,-2) \qquad B(5,8)$

Посмотреть решение

Чтобы найти середину отрезка необходимо непосредственно применить формулу:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{3+5}{2} , \frac{-2+8}{2} \right)$

$\displaystyle M\left(\frac{8}{2} , \frac{6}{2} \right)$

$\displaystyle \bm{M\left(4,3\right)}$

Упражнение 2

Найдите координаты конца отрезка, который начинается в точке А и середина которого равна М.

$A(4,-1) \qquad M(-2,1)$

Посмотреть решение

В этом случае мы знаем координаты начальной точки и середины отрезка. Поэтому подставляем известные нам координаты в формулу середины отрезка:

$\displaystyle \left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)=(x_m,y_m)$

$\displaystyle \left(\frac{4+x_2}{2} , \frac{-1+y_2}{2} \right)=(-2,1)$

И теперь решаем координаты конечной точки отрезка из предыдущего уравнения:

координаты X

$\cfrac{4+x_2}{2} = -2$

$4+x_2 = -2 \cdot 2$

$4+x_2 = -4$

$x_2 = -4-4$

$x_2 = -8$

координаты Y

$\cfrac{-1+y_2}{2} = 1$

$-1+y_2 = 1 \cdot 2$

$-1+y_2 = 2$

$y_2 = 2+1$

$y_2 = 3$

Таким образом, координаты конечного конца сегмента таковы:

$\bm{B(-8,3)}$

Упражнение 3

Дан следующий параллелограмм:

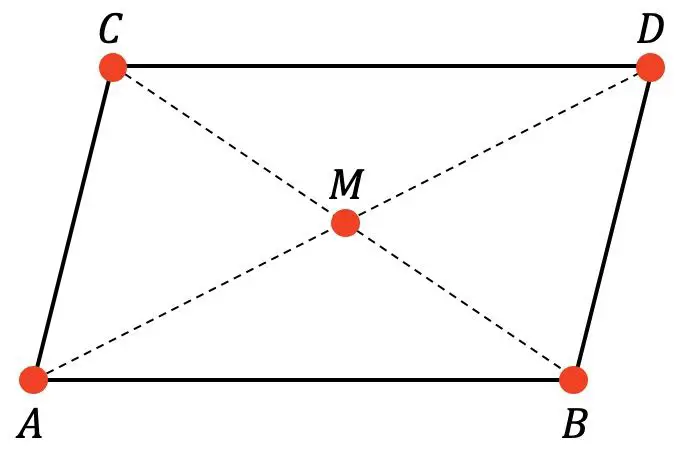
Мы знаем, что M — центр параллелограмма, а координаты точек A, B и C таковы:

$A(1,1) \quad B(5,1) \quad C(7,3)$

На основании этой информации и по формуле средней точки рассчитайте координаты точки D.

Посмотреть решение

Чтобы найти координаты точки D по формуле середины отрезка, необходимо сначала вычислить координаты точки М, затем координаты точки D.

Точка M является серединой отрезка BC, поэтому ее координаты:

$\displaystyle M\left(\frac{5+7}{2} , \frac{1+3}{2} \right)$

$\displaystyle M\left(6,2 \right)$

И как только мы узнаем точку M, мы сможем найти точку D. Точка M также является серединой отрезка AD, поэтому:

$\displaystyle \left(\frac{1+x_2}{2} , \frac{1+y_2}{2} \right)=(6,2)$

Координата X точки D

$\cfrac{1+x_2}{2} = 6$

$1+x_2 = 12$

$x_2 = 11$

Координата Y точки D

$\cfrac{1+y_2}{2} = 2$

$1+y_2 = 4$

$y_2 = 3$

Таким образом, координаты точки D таковы:

$\bm{D(11,3}$

Упражнение 4

Вычислите непрерывное уравнение прямой, перпендикулярной отрезку PQ в его средней точке. Будьте точками

$P(1,4)$

$Q(5,-2).$

Посмотреть решение

Чтобы определить уравнение прямой, нам нужен ее вектор направления и точка, входящая в состав линии.

В этом случае вектор направления прямой будет перпендикулярен вектору

$\vv{PQ}.$

Поэтому мы вычисляем вектор

$\vv{PQ}:$

$\vv{PQ} = Q - P = (5,-2)-(1,4) = (4,-6)$

А найти вектор, перпендикулярный другому, мы можем, меняя компоненты вектора между ними, а затем меняя знак компонента, следовательно:

$\vv{PQ}_\perp =(6,4)$

Теперь у нас есть вектор направления линии, поэтому нам нужна только одна точка, принадлежащая линии. В данном случае инструкция сообщает нам, что линия проходит через середину отрезка, поэтому вычисляем середину по формуле:

$\displaystyle M\left(\frac{1+5}{2} , \frac{4+(-2)}{2} \right)$

$\displaystyle M\left(3,1 \right)$

Наконец, по вычисленной точке и вектору построим непрерывное уравнение линии:

$\cfrac{x-3}{6}=\cfrac{y-1}{4}$

Формула середины отрезка

Что такое середина отрезка?

Как вычислить середину отрезка?

Упражнения решаются в середине сегмента.

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Оставьте комментарий Отменить ответ