Уравнение касательной линии -

В этой статье мы увидим , как найти уравнение касательной к кривой. Кроме того, вы можете тренироваться, решая упражнения разного уровня сложности.

Уравнение касательной к функции в точке

Уравнение касательной к функции f(x) в точке x=x ₀ имеет вид:

$y -y_0= m(x-x_0)$

Где точка P(x ₀ ,y ₀ ) — это точка, в которой касательная и функция совпадают. А наклон касательной m равен производной кривой в точке _x0 , то есть m=f'( _x0 ).

На изображении выше вы можете увидеть кривую

$f(x)$

представлено синей и оранжевой линией, касательной к функции

$f(x)$

$x=x_0$

, поскольку у них есть только эта общая точка. Итак, уравнение этого тангенса имеет вид

$y -y_0= m(x-x_0)$

, а его наклон равен

$m=f'(x_0)$

Как найти уравнение тангенса

Чтобы найти уравнение тангенса к функции в точке, нужно сделать:

Найдите наклон касательной, рассчитав производную функции в точке касания.
Определите точку на касательной.
Найдите уравнение касательной , используя рассчитанный наклон и точку касательной.

Пример уравнения касательной к кривой

После того, как мы ознакомились с теорией уравнения тангенса, давайте посмотрим, как вычислить уравнение тангенса, шаг за шагом решая пример:

Вычислить уравнение касательной к кривой
$f(x)=x^2+x$

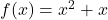
О

$x=1$

.

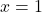
Мы знаем, что уравнение касательного всегда имеет следующий вид:

$y -y_0= m(x-x_0)$

Первое, что нужно сделать, это рассчитать наклон линии. Таким образом, наклон касательной

$m$

, будет значением производной кривой в точке касания x=1, т.е.

$m=f'(1).$

Поэтому мы дифференцируем функцию, а затем вычисляем

$f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

Как только мы узнаем ценность

$m$

, нам нужно найти точку

$(x_0,y_0)$

касательной, чтобы завершить уравнение касательной.

Уравнение касательной и кривой всегда имеют общую точку , которой в данном случае является

$x=1$

. Поэтому, как и кривая

$f(x)$

проходит через эту точку, мы можем найти другую составляющую точки, вычислив

$f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

Таким образом, точка касания:

$P(1,2)$

И кривая, и касательная проходят через эту точку, поэтому мы также можем использовать ее для нахождения уравнения касательной.

Остается только подставить найденные значения наклона и точки касательной в его уравнение:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

Короче говоря, уравнение тангенса:

$\bm{y-2=3(x-1)}$

Вы также можете выразить уравнение касательной прямой с помощью явного уравнения прямой:

$\bm{y=3x-1}$

Ниже вы можете увидеть представленную кривую

$f(x)=x^2+x$

и его линия, касательная к

$x=1,$

$y-2=3(x-1):$

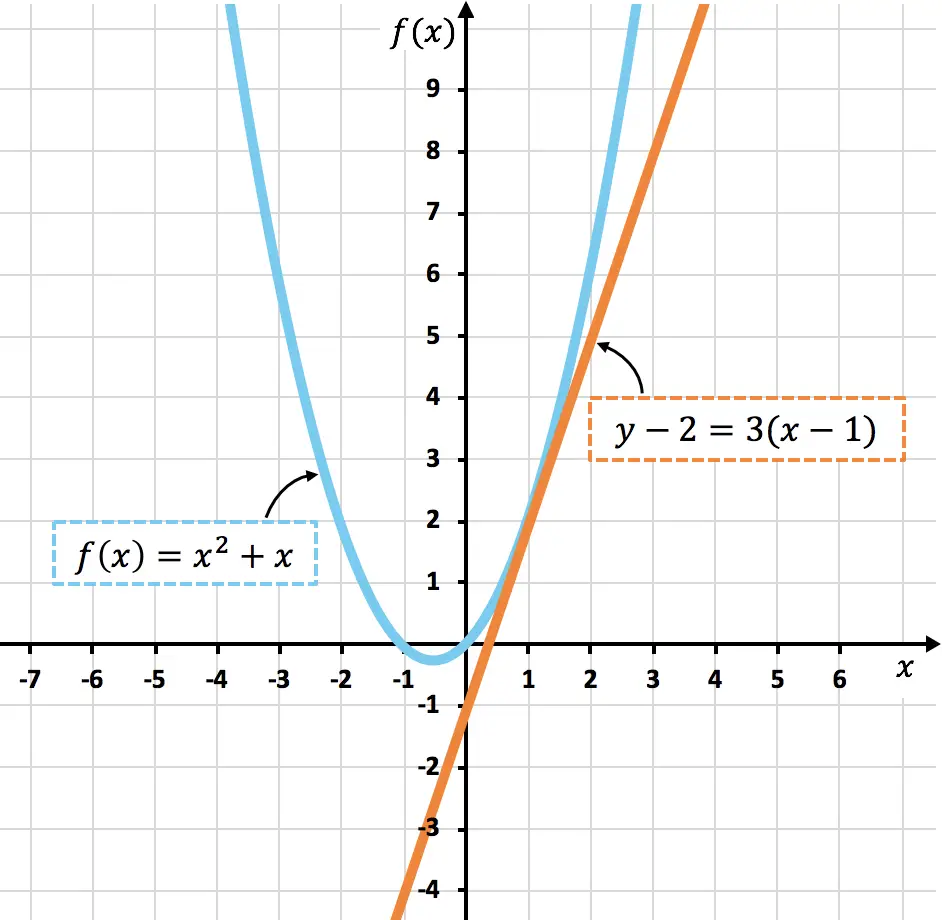
Как видите, кривая

$f(x)=x^2+x$

и касательная

$y-2=3(x-1)$

их объединяет только суть

$(1,2)$

, именно так, как мы рассчитали.

Решенные упражнения на уравнение касательной

Упражнение 1

Вычислить уравнение касательной к кривой

$f(x)=2x^2-4x+3$

$x=2 .$

Посмотреть решение

Уравнение касательной всегда будет иметь следующий вид:

$y-y_0=m(x-x_0)$

Шаг 1. Рассчитайте наклон касательной.

Наклон m — это значение производной кривой в точке касания. Поэтому в этом случае

$m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

Шаг 2. Найдите точку на касательной.

Уравнение касательной и кривой всегда имеют общую точку, которой в данном случае является

$x=2$

. Поэтому, как и кривая

$f(x)$

проходит через эту точку, мы можем найти другую составляющую точки, вычислив

$f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

Таким образом, точка, через которую проходят и кривая, и касательная, является точкой

$(2,3).$

Шаг 3: Напишите уравнение тангенса

Остается только подставить найденные значения наклона и точки касательной в его уравнение:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

Таким образом, уравнение тангенса имеет вид:

$\bm{y -3= 4(x-2)}$

Упражнение 2

Вычислить уравнение касательной к кривой

$\displaystyle f(x)=-3x^2+2x$

в начале координат.

Посмотреть решение

Начало координат относится к точке

$(0,0).$

Поэтому нам необходимо вычислить касательную к функции в точке

$(0,0) .$

Сначала определяем значение наклона касательной, вычисляя производную в начале координат:

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

В этом случае мы уже знаем точку, через которую проходит касательная. Потому что утверждение говорит нам, что линия должна касаться кривой в начале координат, то есть в точке

$(0,0).$

Таким образом, точка, в которой пересекаются кривая и касательная, является точкой

$(0,0).$

Наконец, просто подставьте найденные значения наклона и точки касательной в ваше уравнение:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

В заключение уравнение тангенса имеет вид:

$y -0= 2(x-0)$

$\bm{y = 2x}$

Упражнение 3

Вычислить касательную к кривой

$f(x)=x^2-2x-1$

который параллелен вправо

$y-4x-6=0$

Посмотреть решение

В этой задаче нам говорят, что касательная должна быть параллельна прямой.

$y-4x-6=0 .$

Две прямые параллельны, если они имеют одинаковый наклон. Поэтому касательная должна иметь тот же наклон, что и линия.

$y-4x-6=0.$

Это значит, что нам нужно найти наклон линии

$y-4x-6=0 .$

Для этого очищаем переменную и:

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

Итак, наклон линии

$y=4x+5$

равно 4, так как наклон линии — это число, на которое умножается x, когда y пуст.

Следовательно, наклон касательной тоже должен быть равен 4, поскольку для того, чтобы они были параллельны, они должны иметь одинаковый наклон.

$m=4$

В этом случае они не сообщают нам точку касания кривой и касательной. Но мы знаем, что производная кривой в точке касания равна наклону касательной, т.е.

$m=f'(x_0)$

. Ну как мы можем узнать ценность

$m$

, мы можем найти x ₀ из уравнения

$m=f'(x_0):$

Для этого сначала вычислим производную от

$f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

И теперь мы решаем

$m=f'(x_0)$

знаю это

$m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

И как только мы узнаем координату x точки, мы сможем найти другую координату точки, вычислив

$f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

Таким образом, точка, через которую проходят и кривая, и касательная, является точкой

$(3,2).$

Остается только подставить найденные значения наклона и точки касательной в его уравнение:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

А уравнение тангенса:

$\bm{y -2=4(x-3)}$

Упражнение 4

Вычислить касательную к кривой

$f(x)=2x^2+5x+1$

которая образует угол 45° с осью X.

Посмотреть решение

Постановка задачи говорит нам, что касательная должна образовывать угол 45° с осью X. В этих случаях для определения значения наклона необходимо применить следующую формулу:

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

В операторе не указывается точка касания кривой и касательной линии. Но мы знаем, что производная кривой в точке касания эквивалентна наклону касательной, т.е.

$m=f'(x_0)$

. Поэтому мы можем вычислить x ₀ , решив уравнение

$m=f'(x_0):$

Для этого сначала вычислим производную от

$f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$