Дроби или смешанные числа — очень важное математическое понятие в области исчисления. Поэтому важно знать, как они работают и как решать упражнения с дробями . В этом и состоит цель этой статьи, независимо от того, научитесь ли вы решать операции с дробями и выполнять любые другие упражнения или задачи, включающие числа этого стиля. Тем не менее, начнем с первых упражнений.
Упражнение на действия с дробями
Для начала мы предоставим несколько основных операций, включающих дроби, вам просто нужно их решить и выразить упрощенный результат. Итак, как только вы закончите решать расчеты , рекомендуем вам сравнить результаты и посмотреть поправку, которую мы вам предлагаем. Хотя вы также можете проверить свои результаты с помощью нашего онлайн- калькулятора дробей .
Сложение и вычитание дробей с общим знаменателем.
Ниже вы решены два сложения и два вычитания дробей. Попробуйте решить их самостоятельно и сравните результат. Таким образом, вы рассмотрите механизмы разрешения для этого типа операций:
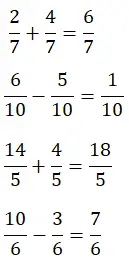
Сложение и вычитание дробей с разными знаменателями.
Теперь немного поднимем уровень, ведь для решения сложения и вычитания дробей с разными знаменателями нам сначала нужно найти НЦМ знаменателей. Таким образом, расчет становится немного сложнее.
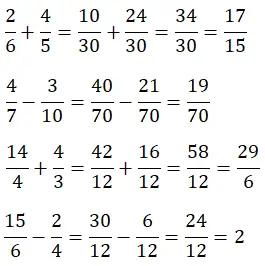
Умножение и деление дробей
В этом разделе вам придется решать задачи умножения и деления дробей, эти операции выполнить очень легко, но вам еще нужно их потренировать. Как и в предыдущих двух разделах, у вас есть по два каждого типа.
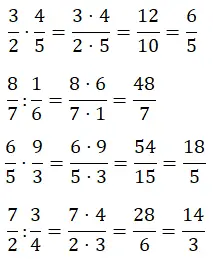
комбинированные дроби
Наконец, вам придется решать комбинированные дроби , которые представляют собой операции, объединенные с дробями. Самым сложным элементом из них является вычисление, так как вам необходимо собрать все свои знания о действиях со смешанными числами, чтобы правильно решить вычисление этого типа.

Упражнение на преобразование десятичных дробей в дроби.
Теперь вам следует попытаться преобразовать следующие десятичные числа в образующую дробь и наоборот. Однако, чтобы сделать это правильно, вам необходимо учитывать тип десятичной дроби (точная, чисто периодическая или смешанная периодическая), поскольку методы преобразования различаются. Если вы не помните эти методы, рекомендуем прочитать нашу статью о дробях , поскольку там мы объясняем все процедуры преобразования десятичных дробей в дроби и наоборот. Ниже вы можете найти некоторые решенные преобразования, мы рекомендуем вам попробовать сделать их самостоятельно:

Упражнение на эквивалентные дроби.
Попрактиковавшись в элементарной арифметике и преобразованиях, пришло время начать с эквивалентных дробей . В этом разделе мы покажем вам несколько дробей, и вам нужно будет найти пары эквивалентных дробей. Таким образом, вы попрактикуетесь в понятии эквивалентности, а также повторите упрощающие дроби .

Упражнение на сравнение дробей
Далее мы покажем вам несколько дробей и вам придется сравнить их с символами «<», «=» и «>». Чтобы решить это упражнение, вам нужно будет найти общий знаменатель и привести обе дроби к этому знаменателю. Таким образом вы сможете увидеть, какой из двух числителей больше, и действовать соответственно:

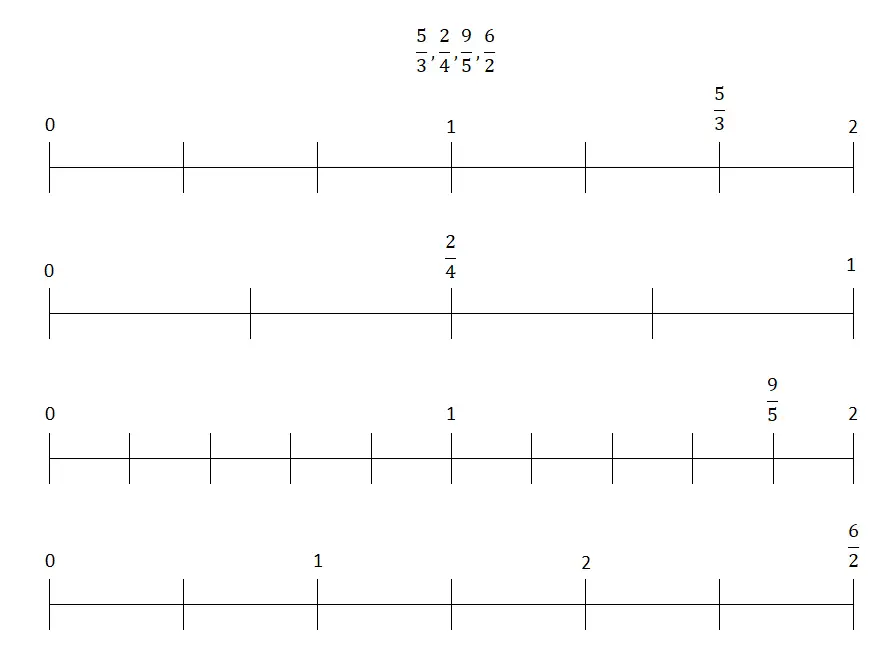
Упражнение на дроби на числовой прямой.
В этом упражнении вам придется упорядочить различные дроби, которые мы собираемся вам дать на числовой прямой , поэтому процедура решения может быть весьма разнообразной. Например, вы можете разделить расстояние между двумя целыми числами на столько частей, сколько указано значением знаменателя, а затем поместить дробь в отрезок , указанный числителем .
Дополнительно вы можете разделить числитель на знаменатель и получить десятичное число, которое позже поместите в строку. Хотя эта вторая процедура гораздо более проста , именно поэтому мы решили выбрать первый метод, который мы объяснили. При этом дроби, которые вам нужно будет разместить справа, следующие:
задачи с дробями
Наконец, мы подошли к последней части этой статьи, в которой мы рассмотрим некоторые проблемы с дробями. Хотя прежде всего мы хотим описать правильную процедуру, которую следует использовать при решении математических задач :
- Поймите проблему. Первый шаг — внимательно прочитать, благодаря чему вы поймете всю проблему. Таким образом вы ознакомитесь со всей информацией, изложенной в декларации. Если вы сделаете эту часть правильно, то вы многого добьетесь, так как будете знать, как проложить решение и все расчеты.
- Постановка проблемы: как только вы узнаете, в чем заключается проблема, вам нужно будет ее представить. Это можно сделать с помощью диаграммы, рисунка или небольшого графического представления данных. На этом этапе вы начнете думать о способах объединения данных и решения проблемы.
- Решите саму задачу. Позже вы можете продолжить решать задачу численно, на этом этапе вам необходимо проверить теории, выдвинутые вами в предыдущем разделе. Именно здесь вы фактически выполняете план действий и получаете результаты, поэтому вам нужно быть очень сосредоточенным.
- Интерпретируйте решения. Наконец, когда у вас уже есть решения, вам нужно будет интерпретировать эти результаты и осмыслить их в контексте проблемы. Этот последний шаг очень важен, и многие люди игнорируют его, поскольку думают, что числового результата достаточно, но на самом деле вам придется обобщить решение в одном предложении.
проблема 1
Если мы хотим наполнить бассейн одним краном, это займет 6 часов, но если мы сделаем это с помощью другого крана, это займет 8 часов. Какая часть бассейна наполнится за 2 часа, если мы воспользуемся обоими кранами одновременно? Выразите результат в виде дроби.
Чтобы решить эту задачу, нам нужно использовать дроби. По сути, мы собираемся отдельно рассчитать, насколько наполнится каждый кран за эти два часа. Итак, первый кран заполнит 1/6 резервуара за один час, а если умножить на два часа, то заполнится 2/6. При этом второй кран за час наполнит 1/8 и нам тоже придется умножить его на 2, при этом у нас будет 2/8.
Наконец, мы сложим две дроби, чтобы получить общий объем заполненного пула. Итак, у нас осталось 2/6 + 2/8 = 7/12 пула.
проблема 2
У нас есть 64 конфеты, но 1/4 из них мы отдаем нашему другу Маркосу. Затем съедаем 3 конфеты и отдаем 2/5 оставшейся суммы нашей подруге Марии. Сколько конфет у нас осталось? Выразите это как целое число.
Сначала нам нужно от общей суммы 64 отнять четверть, затем от полученного результата вычесть 3 и, наконец, отнять две пятых от этого количества конфет. С помощью чего мы можем вычислить это с помощью объединенных дробей:
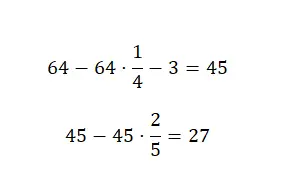
Таким образом, в конце у нас осталось 27 конфет.
проблема 3
У нас есть земельный участок площадью 10 000 м², разделенный на три неравные части. Первая секция представляет собой 3/6 общей площади, а вторая секция равна половине предыдущей. Какая дробь описывает площадь третьего участка? Сколько квадратных метров в каждом секторе?
Первое, что мы сделаем, это вычислим дробь третьего участка, сделаем это посредством очень простого вычитания дробей. Далее рассчитаем площадь каждой секции, вычислив дробь числа, в нашем случае это числовое значение будет равно 10 000. Ниже вы можете увидеть всю процедуру: