На этой странице мы увидим, как умножить число на матрицу. У вас также есть примеры, которые помогут вам в совершенстве это понять, и решенные упражнения, чтобы вы могли практиковаться. Вы также найдете все свойства произведения скаляра и матрицы.
Как умножить число на матрицу?
Чтобы умножить число на матрицу , умножьте каждый элемент матрицы на число.
Пример:

Решенные задачи умножения числа на матрицу
Упражнение 1:
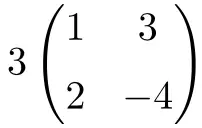
Это умножение скаляра на квадратную матрицу второго порядка:
![Rendered by QuickLaTeX.com \displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-590b79c0fea524b963397181b6f2bea8_l3.png)
Упражнение 2:
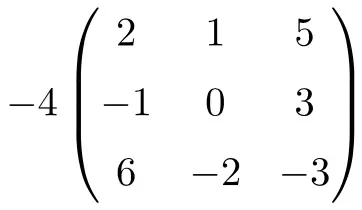
Это произведение числа на квадратную матрицу третьего порядка:
![Rendered by QuickLaTeX.com \displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5042f0f8cd9b7a4d0e28974f793b145b_l3.png)
Упражнение 3:
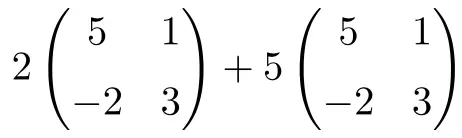
Это операция, объединяющая произведения чисел на матрицы и суммы матриц размерности 2×2:
![Rendered by QuickLaTeX.com \displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56d2a40f021be13a5d92d0c10d353684_l3.png)
Поэтому сначала нужно решить для продуктов:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-068901abef987767025bb01b24579226_l3.png)
И наконец складываем полученные матрицы:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d15ea16036f522af0f23fee0bb796757_l3.png)
Упражнение 4:
Рассмотрим следующие матрицы:
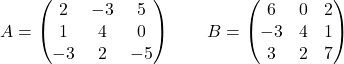
Рассчитать:
![]()
Это операция, сочетающая скалярное умножение со сложением и вычитанием матриц размером 3×3. Кроме того, матрица
![]()
— это единичная матрица, состоящая из 1 на главной диагонали и 0 на остальных элементах:
![Rendered by QuickLaTeX.com \displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dce934040dc05714321dbbeac4e20c73_l3.png)
Поэтому сначала выполняем умножения:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc26f29384abcfb6f08a36b601e4ff61_l3.png)
Добавляем первые две матрицы:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-897ec02d46bc09bdec58d9b3246c6f4d_l3.png)
Наконец, выполняем вычитание матриц:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ddd808a46a137f4c7742545c4f76f46_l3.png)
Если эти упражнения по скалярному произведению матриц были вам полезны, не стесняйтесь попрактиковаться с пошагово решенными упражнениями по сложению матриц и произведению матриц — двум типам матричных операций, которые повторяются чаще.
Свойства произведения числа на матрицу
Как вы хорошо знаете, существует много типов матриц : квадратные матрицы, треугольные матрицы, единичная матрица и т. д. Но, к счастью, все свойства произведения чисел на матрицы справедливы для всех классов матриц.
Вот свойства умножения скаляров и матриц:
- Ассоциативное свойство:
![]()
Посмотрите на следующие две операции, поскольку они дают один и тот же результат независимо от того, как мы умножаем 2 и 3:
![Rendered by QuickLaTeX.com \displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4e9fd568edd5833238d8d21fdf4d1a8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f8ee596b3e2ca16ff1c507717982ee1_l3.png)
- Распределительное свойство относительно сложения скаляров:
![]()
Как вы можете видеть в примере ниже, это то же самое, если мы сначала сложим 1+2, а затем умножим его на матрицу, или если мы умножим матрицу отдельно на 1 и на 2, а затем сложим результаты:
![Rendered by QuickLaTeX.com \displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-025ac9b0851ed93fd0c3870328d6144b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2f54f4d5ae113e2462b752c150b3f43b_l3.png)
- Распределительное свойство относительно сложения матриц:
![]()
Другими словами, сложение двух математических матриц и последующее умножение их на число эквивалентно отдельному умножению двух матриц на одно и то же число с последующим сложением результатов. В примере ниже вы можете проверить:
![Rendered by QuickLaTeX.com \displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdb35d5c66ee525c3d52fe7576e75758_l3.png)
![Rendered by QuickLaTeX.com \displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ef9d3f8f503371fa5f3d2478f728d88_l3.png)
- Свойство нейтрального элемента:
![]()
Следовательно, при умножении матрицы на 1 мы не изменяем матрицу:
![Rendered by QuickLaTeX.com \displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ee2c0afd1bf2904722701caca883125_l3.png)
Это все свойства произведения скаляра и матрицы, так что на этом статья заканчивается. Мы надеемся, что вам понравилось и, прежде всего, вы научились решать умножение чисел на матрицы.
С другой стороны, другие матричные операции, связанные с умножением и которые очень полезны, являются степенями. Здесь мы оставляем вам страницу, на которой вы узнаете, что это такое и как определить степень матрицы , если вам интересно.