Умножение матриц — маторность

На этой странице мы увидим, как умножать матрицы размеров 2×2, 3×3, 4×4 и т. д. Мы объясним процедуру умножения матриц шаг за шагом на примере, затем вы найдете решенные упражнения, чтобы вы также могли попрактиковаться. Наконец, вы узнаете, когда две матрицы нельзя перемножить, и все свойства этой матричной операции.

Как перемножить две матрицы?

Давайте посмотрим процедуру умножения двух матриц на примере:

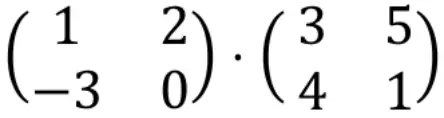
Чтобы вычислить умножение матрицы, строки левой матрицы необходимо умножить на столбцы правой матрицы.

Итак, сначала нам нужно умножить первую строку на первый столбец. Для этого мы поочередно умножаем каждый элемент первой строки на каждый элемент первого столбца и складываем результаты. Итак, все это будет первым элементом первой строки результирующего массива. Посмотрите порядок действий:

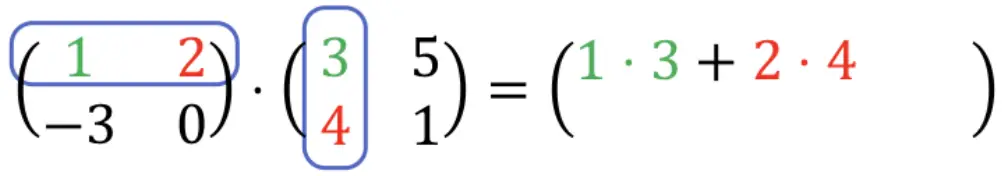
как решать умножение матриц 2х2, действия с матрицами

1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. Итак:

Теперь нам нужно умножить первую строку на второй столбец . Поэтому повторяем процедуру: умножаем каждый элемент первой строки по одному на каждый элемент второго столбца и складываем результаты. И все это будет вторым элементом первой строки результирующего массива:

1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. Итак:

После того как мы заполнили первую строку полученной матрицы, мы переходим ко второй строке. Поэтому мы умножаем вторую строку на первый столбец, повторяя процедуру: мы умножаем по одному каждый элемент второй строки на каждый элемент первого столбца и складываем результаты:

-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. Еще:

Наконец, мы умножаем вторую строку на второй столбец . Всегда по одной и той же процедуре: каждый элемент второй строки умножаем по одному на каждый элемент второго столбца и складываем результаты:

-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. Еще:

И на этом умножение двух матриц заканчивается. Как вы видели, вам нужно умножить строки на столбцы, всегда повторяя одну и ту же процедуру: умножить каждый элемент строки на каждый элемент столбца по одному и сложить результаты.

Решенные упражнения на умножение матриц

Упражнение 1

Решите следующее матричное произведение:

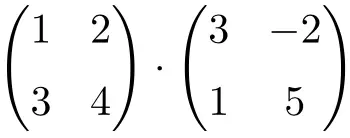
упражнение поэтапно решено произведение матриц 2х2, операции с матрицами

посмотреть решение

Это произведение матриц второго порядка:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

Чтобы решить матричное произведение, необходимо умножить строки левой матрицы на столбцы правой матрицы.

Итак, сначала мы умножаем первую строку на первый столбец. Для этого мы поочередно умножаем каждый элемент первой строки на каждый элемент первого столбца и складываем результаты. И все это будет первым элементом первой строки результирующего массива:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

Теперь умножим первую строку на второй столбец, чтобы получить второй элемент первой строки результирующей матрицы:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

Переходим ко второй строке, поэтому умножаем вторую строку на первый столбец:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

Наконец, мы умножаем вторую строку на второй столбец , чтобы вычислить последний элемент таблицы:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

Итак, результат умножения матрицы:

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

Упражнение 2

Найдите результат следующего умножения квадратной матрицы 2×2:

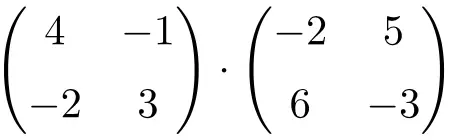
Упражнение решено пошагово по умножению матриц 2х2, матричным операциям.

посмотреть решение

Это произведение матриц размерности 2×2.

Чтобы решить умножение, необходимо умножить строки левой матрицы на столбцы правой матрицы:

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

Упражнение 3

Вычислите следующее умножение матрицы 3×3:

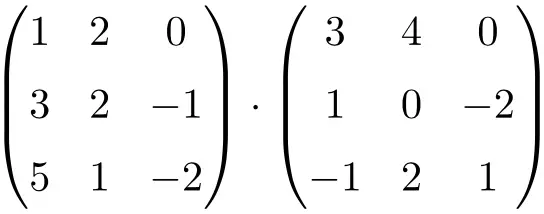
упражнение решено поэтапно умножение матриц 3х3, матричные операции

посмотреть решение

Чтобы выполнить умножение матрицы 3×3, необходимо умножить строки левой матрицы на столбцы правой матрицы:

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

Упражнение 4

учитывая матрицу

$A$

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

Рассчитать:

$\displaystyle 2A\cdot A^t$

посмотреть решение

Сначала мы рассчитаем транспонированную матрицу

$A$

сделать умножение. И чтобы сделать транспонированную матрицу, нам нужно преобразовать строки в столбцы. То есть первая строка матрицы становится первым столбцом матрицы, а вторая строка матрицы становится вторым столбцом матрицы. Еще:

$\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Таким образом, матричная операция остается:

$\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Теперь мы можем провести расчеты. Сначала мы рассчитываем

$2A$

(хотя мы также можем сначала вычислить

$A \cdot A^t$

$\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

И, наконец, решаем произведение матриц:

$\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

Упражнение 5

Рассмотрим следующие матрицы:

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

Рассчитать:

$\displaystyle A\cdot B - B \cdot A$

посмотреть решение

Это операция, сочетающая вычитание с умножением матриц второго порядка:

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

Сначала вычисляем умножение слева:

$\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

Теперь решаем умножение справа:

$\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}$

И наконец вычитаем матрицы:

$\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

Когда нельзя перемножить две матрицы?

Не все матрицы можно умножать. Чтобы перемножить две матрицы, количество столбцов в первой матрице должно совпадать с количеством строк во второй матрице.

Например, следующее умножение невозможно выполнить, поскольку первая матрица имеет 3 столбца, а вторая матрица — 2 строки:

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

Но если поменять порядок, их можно будет умножить. Поскольку первая матрица имеет два столбца, а вторая матрица имеет две строки:

$\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}$

Свойства умножения матрицы

Этот тип матричной операции имеет следующие характеристики:

Умножение матриц ассоциативно:

$\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

Умножение матриц также обладает распределительным свойством:

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

Произведение матриц не коммутативно:

$\displaystyle A \cdot B \neq B \cdot A$

Например, следующее умножение матрицы дает результат:

$\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}$

Но результат произведения будет другим, если поменять порядок умножения матриц:

$\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}$

Кроме того, любая матрица, умноженная на единичную матрицу, дает ту же самую матрицу. Это называется свойством мультипликативной идентичности:

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

Например:

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

Наконец, как вы уже могли догадаться, любая матрица, умноженная на нулевую матрицу, равна нулевой матрице. Это называется мультипликативным свойством нуля:

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

Например:

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

Умножение матрицы

Как перемножить две матрицы?

Решенные упражнения на умножение матриц

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Когда нельзя перемножить две матрицы?

Свойства умножения матрицы

Оставьте комментарий Отменить ответ