Угол между прямой и плоскостью

Здесь вы узнаете, как рассчитывается угол между линией и плоскостью. Вы также сможете увидеть примеры и, кроме того, попрактиковаться в упражнениях, пошагово решающих углы между линиями и плоскостями.

Каков угол между прямой и плоскостью?

Угол между прямой и плоскостью — это угол между прямой и ее ортогональной проекцией на плоскость.

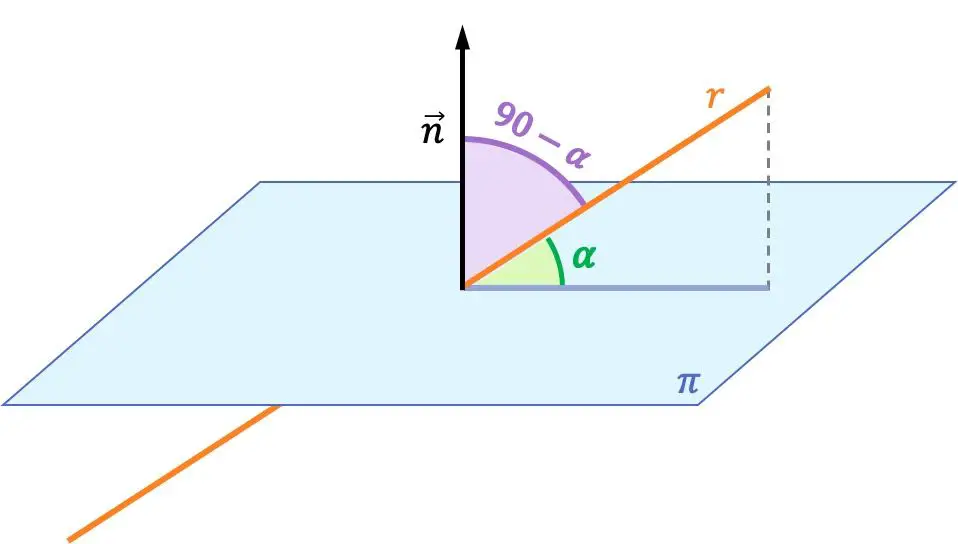
Угол между прямой и плоскостью является дополнением угла между указанной линией и вектором, нормальным к плоскости. Следовательно, угол между линией и плоскостью вычисляется по углу между вектором направления линии и вектором нормали к плоскости.

Формула угла между прямой и плоскостью

Чтобы вывести формулу угла между плоскостью и прямой, нужно знать, как найти угол между двумя векторами . На связанной странице вы найдете объяснение, а также примеры и упражнения, решаемые шаг за шагом, поэтому, если вы не помните, как это сделать, рекомендуем вам посмотреть.

Таким образом, поскольку угол между линией и плоскостью дополняет угол между вектором направления указанной линии

$(\vv{\text{v}}_r)$

и вектор нормали к указанной плоскости

$(\vv{n})$

, из формулы угла между двумя векторами заключаем, что угол между прямой и плоскостью эквивалентен следующему выражению:

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Следовательно, формула угла между прямой и плоскостью :

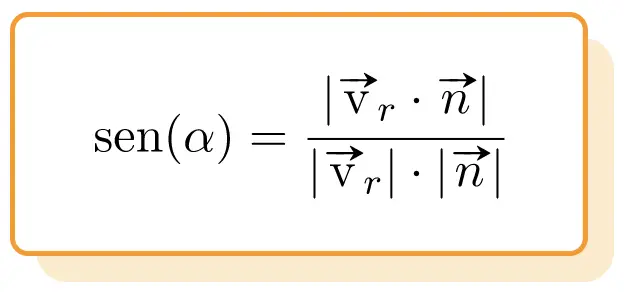
Золото:

$\vv{\text{v}}_r$

– прямой вектор прямой.
$\vv{n}$

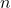
– вектор нормали к плоскости.

Пример расчета угла между линией и плоскостью

Чтобы вы могли увидеть, как решить задачу такого типа, вот пример расчета угла между линией и плоскостью:

Вычислите угол, образованный линией
$r$

с самолетом

$\pi.$

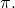
Пусть их уравнения будут:

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

Линия выражается в виде параметрических уравнений, поэтому ее вектор направления равен:

$\vv{\text{v}}_r = (-1,4,-3)$

С другой стороны, плоскость определяется в виде неявного (или общего) уравнения, поэтому ее вектор нормали равен:

$\vv{n} = (1,-1,4)$

Таким образом, как только мы знаем вектор направления линии и вектор нормали плоскости, мы применяем формулу угла между линией и плоскостью:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Подставим векторы в формулу:

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

И делаем расчеты:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

Наконец, инвертируем синус с помощью калькулятора и находим значение угла:

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

Таким образом, угол между линией и плоскостью составляет примерно 51,80°.

Надо учитывать, что если мы когда-нибудь получим результат 0°, это означает, что линия и плоскость параллельны или что линия содержится в плоскости. А если угол равен 90°, это означает, что линия и плоскость перпендикулярны.

Решены задачи об угле между прямой и плоскостью.

Упражнение 1

Найдите угол, образованный прямой

$r$

с самолетом

$\pi.$

Пусть их уравнения будут:

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

посмотреть решение

Линия выражается в виде непрерывного уравнения, поэтому ее вектор направления равен:

$\vv{\text{v}}_r = (2,-1,-3)$

С другой стороны, плоскость имеет форму неявного (или общего) уравнения, поэтому ее вектор нормали равен:

$\vv{n} = (3,1,2)$

Итак, как только мы знаем вектор направления линии и вектор нормали плоскости, мы используем формулу угла между линией и плоскостью:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

Наконец, инвертируем синус и находим значение угла:

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

Следовательно, угол между линией и плоскостью равен 4,10°.

Упражнение 2

Определить угол, образованный прямой

$r$

с самолетом

$\pi.$

Пусть их уравнения будут:

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

посмотреть решение

Линия выражается с помощью неявных (или общих) уравнений, поэтому необходимо найти вектор направления линии путем вычисления векторного произведения векторов, нормальных к двум плоскостям, которые определяют линию:

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

С другой стороны, вектор, нормаль к плоскости:

$\vv{n} = (-4,2,0)$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

Наконец, инвертируем синус и находим значение угла:

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

Следовательно, угол между линией и плоскостью равен 46,33 градуса.

Упражнение 3

Найдите по формуле угла между прямой и плоскостью значение

$k$

необходимо для права

$r$

и самолет

$\pi$

быть параллельным.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

посмотреть решение

Во-первых, линия выражается в виде векторного уравнения, поэтому ее вектор направления равен:

$\vv{\text{v}}_r = (4,-1,3)$

С другой стороны, плоскость имеет форму общего уравнения, поэтому ее вектор нормали равен:

$\vv{n} = (4,3,k)$

Итак, чтобы два геометрических элемента были параллельны, угол между ними должен быть равен нулю. Следовательно, формула угла между прямой и плоскостью имеет вид:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

Таким образом, скалярное произведение вектора направления линии и вектора нормали должно быть равно нулю. И из этого уравнения мы можем определить значение неизвестного

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

Наконец, если эта статья оказалась для вас полезной, вас, вероятно, также интересует, как найти угол между двумя плоскостями . На странице ссылок вы найдете очень подробное объяснение, а также необходимую формулу для расчета угла между двумя разными плоскостями, а также вы сможете увидеть примеры и упражнения, решенные шаг за шагом, чтобы иметь возможность практиковаться и понимать. как это сделано идеально.

Угол между линией и плоскостью

Каков угол между прямой и плоскостью?

Формула угла между прямой и плоскостью

Пример расчета угла между линией и плоскостью

Решены задачи об угле между прямой и плоскостью.

Упражнение 1

Упражнение 2

Упражнение 3

Оставьте комментарий Отменить ответ