Здесь вы узнаете, как решать тригонометрические пределы. Вы сможете увидеть несколько примеров пределов тригонометрических функций и даже попрактиковаться, решая пошаговые упражнения по тригонометрическим пределам.
Что такое тригонометрические пределы?
Тригонометрические пределы — это пределы, рассчитанные для тригонометрических функций. Для решения тригонометрических пределов необходимо применить предварительную процедуру, поскольку они обычно приводят к неопределенностям.
Кроме того, бесконечных пределов тригонометрических функций не существует, поскольку они являются периодическими функциями. То есть его графики непрерывно периодически повторяются, не стремясь к определенному значению.
Тригонометрические предельные формулы
Все тригонометрические пределы рассчитываются по следующим двум формулам:
![]()
Если мы попытаемся вычислить предел путем подстановки, мы получим нулевую неопределенность между нулями:
![]()
Но эту тригонометрическую формулу можно продемонстрировать, рассчитав значения функции ближе и ближе к x=0 (углы в радианах).
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ccd668acef73b9140a0cbbb9c1d53ad3_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-66152efc3ce1fa761186a65db677af27_l3.png)
Два боковых предела тригонометрической функции дают 1, поэтому предел в точке x=0 равен 1:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8af649189957b154866097e315f7cb92_l3.png)
Таким образом, тригонометрический предел синуса x, деленного на x при стремлении x к 0, равен 1.
Эту формулу также можно применить для нескольких углов:
![]()
![]()
Если мы попытаемся найти предел прямой подстановкой, мы получим неопределенную форму нуля между нулями:
![]()
Но мы можем проверить равенство по приведенной выше формуле. Для этого необходимо сначала числитель и знаменатель дроби умножить на 1 плюс косинус х:
![]()
Теперь у нас есть заметная идентичность числителя дроби, поэтому мы можем его упростить:
![]()
![]()
Отталкиваясь от основного тригонометрического тождества, перепишем числитель:
![]()
![]()
Таким образом, мы можем преобразовать дробь в произведение дробей:
![]()
![]()
Используя свойства пределов, мы можем преобразовать приведенное выше выражение в произведение пределов:
![]()
Используя приведенную выше формулу, мы можем легко упростить тригонометрический предел:
![]()
![]()
![]()
И, наконец, вычисляем получившийся лимит:
![]()
Таким образом, проверяется формула тригонометрического предела:
![]()
Как и другую формулу, ее также можно использовать для нескольких углов:
![]()
Следовательно, чтобы решить тригонометрические пределы, мы должны использовать арифметику, чтобы преобразовать функции и получить выражения, подобные этим. Таким образом, мы можем использовать одну из двух формул и найти значение предела.
С другой стороны, иногда нам может потребоваться применить определенные тригонометрические тождества, поэтому мы оставляем все приведенные ниже формулы на ваше усмотрение.
Формула, связывающая три основных тригонометрических отношения:
![]()
Основное тригонометрическое тождество:
![]()
Тригонометрические соотношения, выведенные из фундаментальных:
![]()
![]()
Противоположные углы:
![]()
![]()
![]()
Сумма двух углов:
![]()
![]()
![]()
Разница двух углов:
![]()
![]()
![]()
Двойной угол:
![]()
![]()
![]()
Половина угла:
![]()
![]()
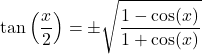
Сложение и вычитание синуса и косинуса:
![]()
![]()
![]()
![]()
Произведение синусов и косинусов:
![]()
![]()
![]()
Чтобы вы могли увидеть, как именно рассчитываются тригонометрические пределы, мы собрали пошаговый пример ниже.
Пример тригонометрического предела
Давайте посмотрим, как решается тригонометрический предел, на следующем примере:
![]()
Пытаясь вычислить тригонометрический предел, получаем неопределенность нуля между нулями:
![]()
➤ См.: нулевые пределы между нулевым
Поэтому для решения предела необходимо преобразовать тригонометрическую функцию. Тангенс равен синусу, разделенному на косинус, поэтому:
![]()
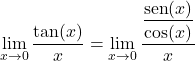
Теперь мы можем выразить функцию в виде произведения, применив свойства дробей:
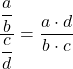
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd10c321c3b7dc40698b318c7187a3c4_l3.png)
Используя свойства пределов, мы можем преобразовать предел двух умноженных функций в произведение двух пределов:
![]()
Как мы показали выше, первый тригонометрический предел дает 1:
![]()
![]()
Итак, просто выполните следующий расчет:
![]()
Решенные упражнения на тригонометрические пределы
Упражнение 1
Решите следующий тригонометрический предел:
![]()
Сначала попытаемся вычислить тригонометрический предел прямым вычислением:
![]()
Но мы получаем нулевую неопределенность. Итак, нам нужно применить преобразования к функции.
Во-первых, мы просто оставим x в знаменателе, выполнив следующие действия:
![]()
Теперь умножим и разделим дробь на 4, чтобы получить выражение, с помощью которого можно применить первую формулу тригонометрических пределов:
![]()
Наконец, мы применяем формулу, показанную в начале, и решаем тригонометрический предел:
![]()
![]()
Упражнение 2
Вычислите следующий тригонометрический предел:
![]()
Сначала попытаемся найти тригонометрический предел:
![]()
Но неопределенная форма соответствует нулю.
Затем преобразуем тангенс в частное синуса и косинуса:
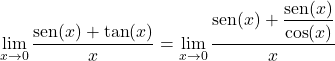
Умножаем и делим на косинус x:
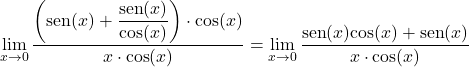
Берем общий множитель в числителе и разделяем тригонометрический предел на два:
![]()
И, наконец, находим результат тригонометрического предела:
![]()
Упражнение 3
Решите предел следующей тригонометрической функции, когда x приближается к нулю:
![]()
Выполняя прямой расчет, мы получаем неопределенный предел 0 между 0:
![]()
Таким образом, мы упростим предел, разделив каждое слагаемое на тангенс x:
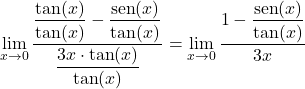
Во-вторых, мы можем вывести из фундаментального тригонометрического тождества, что дробь числителя эквивалентна косинусу x:
![]()
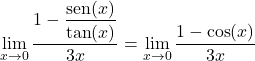
А применив вторую формулу, продемонстрированную в теории тригонометрических пределов, мы легко можем решить этот предел:
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1ee20bc86ad7559fcda3d6bad3c9b27_l3.png)
Упражнение 4
Определите решение следующего тригонометрического предела в точке x=0:
![]()
Если мы попытаемся решить предел, мы найдем неопределенную форму 0/0:
![]()
Алгебраическое выражение для числителя можно переписать, используя тригонометрическое тождество синуса двойного угла:
![]()
![]()
Теперь разделим предел тригонометрической функции на произведение:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc650634075435b782f1e7b921b77c02_l3.png)
И, наконец, решаем тригонометрический предел, применяя свойства пределов:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c26ba3032828541e69e4bd976ac4f96_l3.png)