На этой странице объясняется, как сложить два вектора на плоскости графически и численно. Существует 3 способа сложения их графически: параллелограмм, метод «голова к хвосту» и метод многоугольника. Кроме того, вы также найдете решенные упражнения на сложение векторов и все свойства сложения векторов.
Как сложить два вектора графически?
По сути, существует два способа добавления векторов из их графического представления. С обеими фигурами получается один и тот же результат, но некоторые предпочитают складывать их методом «голова-хвост» , а другие — методом параллелограмма . Поэтому мы объясним вам два метода, чтобы вы выбрали тот, который предпочитаете. 😉
С другой стороны, эти два метода используются для добавления двух векторов, но что произойдет, если мы захотим добавить более двух векторов? Поэтому необходимо использовать метод многоугольника , который заключается в последовательном использовании метода параллелограмма. Его объяснение вы также найдете после методов «голова-хвост» и «параллелограмм».
Метод или правило параллелограмма
Правило параллелограмма или метод параллелограмма (или закон параллелограмма) — это графическая процедура, позволяющая очень простым способом найти сумму двух векторов. Для применения этого процесса необходимо выполнить следующие шаги:
- Сначала мы рисуем векторы и располагаем их в одной и той же точке приложения, то есть помещаем начала обоих векторов в одну и ту же точку.
- Затем мы рисуем в конце одного вектора линию, параллельную другому вектору. И повторяем шаг с другим вектором. Таким образом, мы получим рисунок параллелограмма (отсюда и название правила).
- Наконец, результатом суммы будет вектор, идущий от общего начала координат до точки пересечения двух параллельных прямых.
Посмотрите на следующий общий пример, в котором два вектора складываются по правилу параллелограмма:

Результатом суммы векторов является диагональ параллелограмма, который они образуют со своими параллелями.
метод головы и хвоста
Метод головы и хвоста , также известный как метод треугольника , — это еще одна процедура, с помощью которой два вектора можно сложить графически. В этом случае необходимо выполнить следующие действия:
- Переместите добавленный вектор и поместите его так, чтобы его начало находилось прямо в конце другого добавленного вектора.
- Результатом сложения векторов является сегмент, идущий от начала первого добавленного вектора до конца другого вектора. Если вы присмотритесь, то увидите, что треугольник состоит из двух добавленных векторов и добавленного вектора.
Вот пример сложения векторов методом «голова к хвосту»:
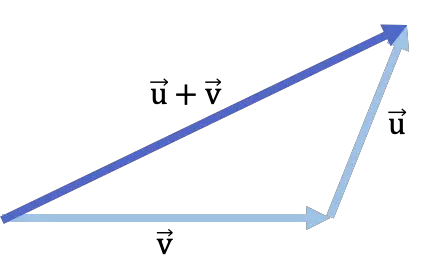
полигональный метод
После того, как мы увидели, как графически решить сумму двух векторов, мы увидим, как это делается, когда у нас более двух векторов.
Если вы хотите сложить три или более векторов, существует способ ускорить вычисление операции. Этот метод называется методом многоугольника и заключается в последовательном применении метода «голова к хвосту»:
- Сначала нам нужно разместить каждый вектор после другого так, чтобы начало одного вектора совпадало с концом другого вектора. Порядок, в котором мы их размещаем, не имеет значения.
- Результатом суммы является вектор, полученный путем соединения начала первого вектора с концом последнего вектора.
Посмотрите на следующий пример, где добавляются 4 вектора:
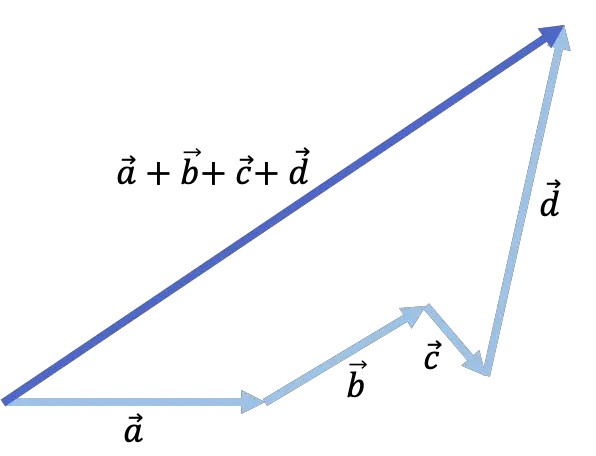
Вычислить сумму двух векторов численно
Как только мы научимся складывать векторы геометрически, мы увидим, как вычислять сумму векторов численно или алгебраически.
Чтобы численно сложить два вектора, необходимо сложить их соответствующие компоненты. Другими словами, координаты X двух векторов складываются друг с другом и совпадают с координатами Y.
![]()
![]()
Например, сумма векторов
![]()
И
![]()
Восток:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(1,2) +(5, 3) \\[2ex] & = (1+5,2+3) \\[2ex] & = \bm{(6,5)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c0813ac0f7ad7fafa1f20b6284430a5_l3.png)
С другой стороны, мы должны иметь в виду, что векторное сложение двух векторов — это не то же самое, что сложение модулей векторов, на самом деле результаты совершенно разные. Вы можете увидеть различия между двумя операциями в свойствах векторной величины (также называемой векторной величиной).
Добавить векторные свойства
Сложение векторов имеет следующие характеристики:
- Ассоциативное свойство : размещение круглых скобок между суммой нескольких векторов не изменяет результат операции.
![]()
- Коммутативное свойство . В отличие от вычитания векторов, результат сложения двух векторов не зависит от порядка, в котором они складываются.
![]()
- Свойство противоположного элемента : сумма вектора плюс его противоположность, то есть его отрицание, равна 0.
![]()
- Свойство нейтрального элемента : очевидно, что любой вектор плюс нулевой или нулевой вектор эквивалентен самому вектору:
![]()
Решенные задачи сложения векторов
Упражнение 1
Вычислить сумму векторов графически
![]()
И
![]()
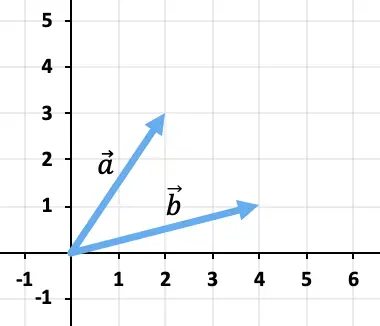
Чтобы сложить два вектора, мы воспользуемся правилом головы и хвоста. Поэтому мы поместим начало вектора
![]()
в конце вектора
![]()
, а сумма будет вектором, идущим от начала координат до конца
![]()
Следовательно, результат сложения векторов:
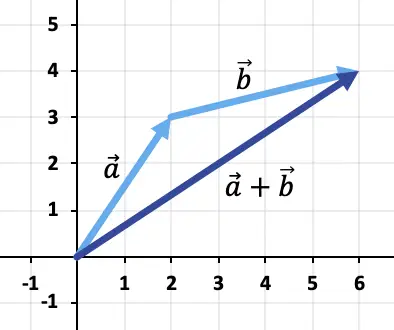
Упражнение 2
Решить сумму векторов графически
![]()
И
![]()
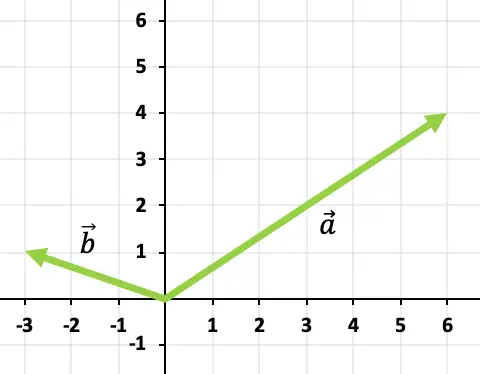
Чтобы сложить два вектора, мы воспользуемся правилом «голова-хвост». Таким образом, мы найдем начало вектора
![]()
в конце вектора
![]()
, а вектором суммы будет тот, который идет от начала осей до конца
![]()
Следовательно, результат сложения векторов:
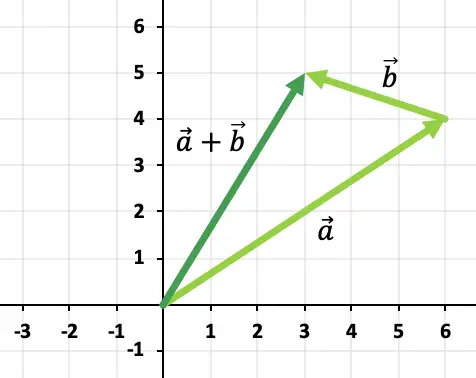
Упражнение 3
Графически определим вектор, полученный в результате сложения всех векторов, представленных на графике:
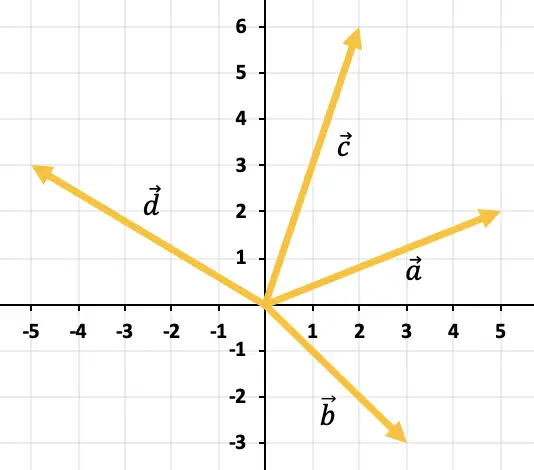
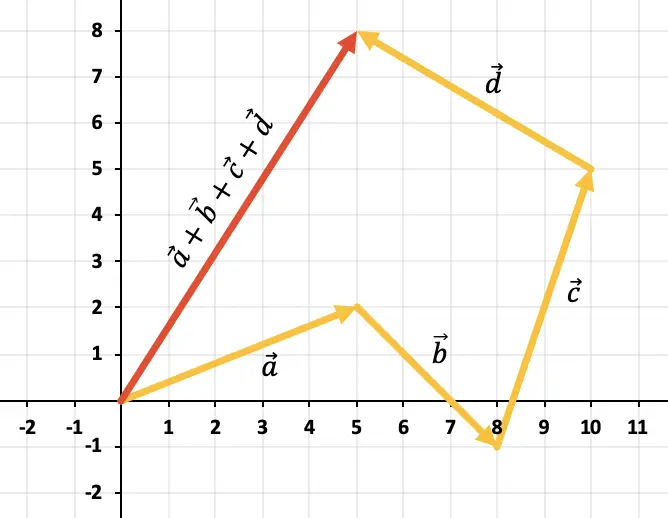
Чтобы добавить из графика более 2 векторов, необходимо использовать правило многоугольника. Поэтому мы должны перемещать векторы так, чтобы они оставались непрерывными, то есть один за другим (порядок не имеет значения). Таким образом, сумма всех векторов будет вектором, идущим от начала первого вектора до конца последнего вектора.
Таким образом, результатом суммы четырех векторов является вектор, представленный красным:
Упражнение 4
Найдите численно сумму следующих векторов:
![]()
Чтобы численно сложить два вектора, необходимо добавить их соответствующие координаты:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}+\vv{b}& =(3,-2)+(-4,6) \\[2ex] & = (3+(-4) ,-2+6)\\[2ex] & =\bm{(-1,4)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e6299484debe49023b686839df40f88b_l3.png)
Упражнение 5
Аналитически вычислите сумму следующих векторов:
![]()
Чтобы численно добавить векторы, необходимо добавить их соответствующие координаты:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{a}+\vv{b}+\vv{c}+\vv{d}& =(-1,3)+(4,0)+(2,-5)+(3,-2) \\[2ex] & = (3,3)+(2,-5)+(3,-2) \\[2ex] & = (5,-2)+(3,-2)\\[2ex] & =\bm{(8,-4)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-05b7c1606bfa3d94d080163a40dc4412_l3.png)