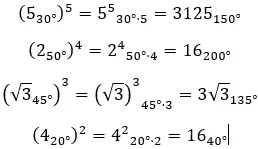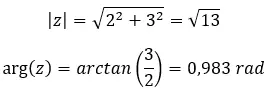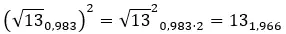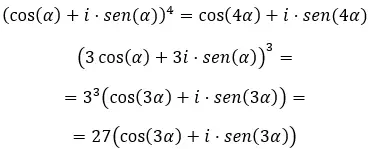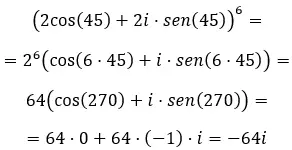Вычислить степени комплексных чисел довольно легко, если знать правильный метод. Поэтому в этой статье мы объясним, как решать комплексные степени тремя способами: для комплексных чисел в биномиальной форме, в полярной форме и в тригонометрической форме.
Как определить степень комплексного числа?
Как мы говорили во введении, при работе со сложными полномочиями могут возникнуть три ситуации. Первый и самый простой — когда нам дано число в полярной форме . Второй — когда нам дано число в биномиальной форме, а третий — когда нам дано число в тригонометрической форме.
Другими словами, при работе с комплексами в полярной форме упражнение можно решить быстрее. Поэтому рекомендуется преобразовать рассматриваемое число в полярную форму. Но на самом деле все методы легко решить . При этом мы объясним вам, как разрешаются все случаи, и предложим вам упражнение.
Степени комплексных чисел в полярной форме
Когда мы хотим решить комплексные степени в полярной форме , мы просто повышаем модуль до любого и умножаем аргумент на n. Выражаясь математически, получаем следующую формулу:
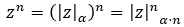
Вот несколько примеров, так что вы можете попытаться решить их самостоятельно:
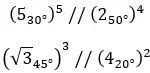
Степени комплексных чисел в биномиальной форме
С другой стороны, когда мы хотим решить комплексные степени в биномиальной форме , мы можем использовать два разных метода. Первый касается решения степени «алгебраическим» способом (решение так, как если бы я был переменной). Вторая система заключается в преобразовании биномиальной формы в полярную, а затем следовании предыдущей процедуре.
Если вы не знаете, как перейти от биномиальной формы к полярной, мы очень доходчиво объясняем вам это в нашей статье о комплексных числах . Хотя, сейчас мы это быстро увидим на примере.
Попробуйте решить следующую комплексную степень: (2 + 3i) 2 .
Степени комплексных чисел в тригонометрической форме
Наконец, когда мы хотим решить комплексные степени в тригонометрической форме , мы должны использовать известную формулу Муавра. Что написано так:
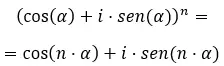
Зная эту формулу, попробуйте решить следующие упражнения:

Узнайте больше о сложных полномочиях
- Комплексные числа
- Свойства комплексов
- Операции над комплексными числами
- сложные корни