На этой странице мы увидим, как складывать и вычитать матрицы . У вас также есть примеры, которые помогут вам в совершенстве это понять, и решенные упражнения, чтобы вы могли практиковаться. Вы также найдете все свойства сложения матриц.
Как складывать и вычитать матрицы?
Чтобы вычислить сложение (или вычитание) двух матриц, необходимо сложить (или вычесть) элементы, занимающие в матрицах одинаковое положение.
Примеры:
Обратите внимание: чтобы сложить или вычесть две матрицы, они должны иметь одинаковую размерность. Например, невозможно сложить следующие матрицы, поскольку первая — матрица 2×2, а вторая — матрица 3×2:
![\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-082c648e15685c4ddeac2cc2da502d96_l3.png "Rendered by QuickLaTeX.com")
Решенные упражнения на сложение и вычитание матриц.
Упражнение 1
Вычислите следующую сумму матриц 2×2:
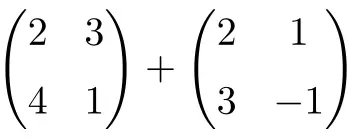
Это сумма двух квадратных матриц размерности 2×2:
![\displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d9428ad89a6bd149d5e63bc500879ac_l3.png "Rendered by QuickLaTeX.com")
Упражнение 2
Выполните следующее вычитание матрицы:
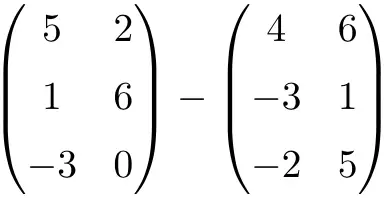
Это вычитание двух матриц размерности 3×2:
![\displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c371e1f01df59f4b8abb018e476e66d7_l3.png "Rendered by QuickLaTeX.com")
Упражнение 3
Найдите результат следующей матричной суммы размером 3×3:
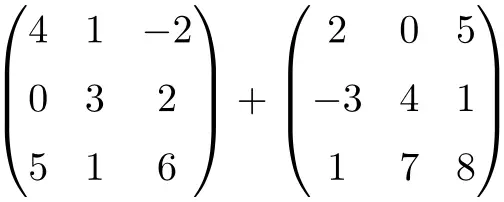
Это сумма двух квадратных матриц порядка 3×3:
![\displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-280299cb0b37e1a585466c4570439ec4_l3.png "Rendered by QuickLaTeX.com")
Упражнение 4
Вычислите следующее сложение и вычитание квадратных матриц второго порядка:
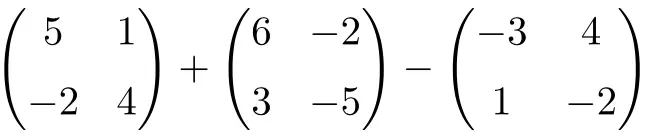
Это операция, совмещенная со сложением и вычитанием квадратных матриц второго порядка:
![\displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9fa4dba7699c0035ce5081756b4f62e_l3.png "Rendered by QuickLaTeX.com")
Итак, сначала добавляем матрицы слева:
![\displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e1544e4da9d5ad2ea3ec2e4ad0326023_l3.png "Rendered by QuickLaTeX.com")
А затем вычисляем вычитание матриц:
![\displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bd7f32fc7c9429fdfc3b5b745e85975c_l3.png "Rendered by QuickLaTeX.com")
Упражнение 5
Решите следующую матрицу сложения и вычитания:
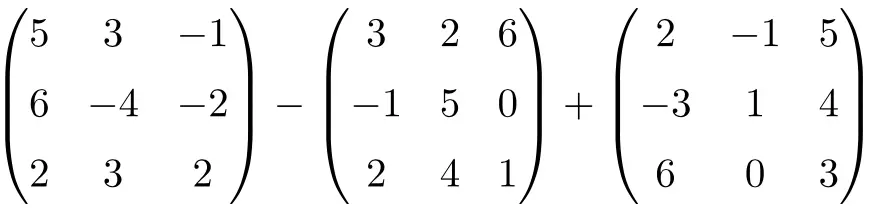
Это комбинированная операция вычитания и сложения квадратных матриц третьего порядка:
![\displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae66268adcd61258654056815542cf58_l3.png "Rendered by QuickLaTeX.com")
Сначала решаем вычитание матрицы:
![\displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4401b28babce2beaaa6f840c4ed8c959_l3.png "Rendered by QuickLaTeX.com")
И, наконец, добавляем матрицы:
![\displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffba1ade3d98c434960b54fc0c7ffe1f_l3.png "Rendered by QuickLaTeX.com")
Теперь, когда вы знаете, как складывать и вычитать матрицы, самое время узнать, как умножать матрицы — несомненно, самую важную из матричных операций. Также вы найдете решенные пошаговые упражнения на умножение матриц для практики, как и на всех страницах этого сайта. 😉
Добавить свойства матрицы
Сложение матриц имеет следующие характеристики:
- Сложение матриц обладает коммутативным свойством :
Следовательно, порядок добавления матриц тот же. Чтобы продемонстрировать это, мы добавим две матрицы, изменив их порядок, и вы увидите, что результат тот же.
Поэтому мы приступаем к сложению двух матриц в определенном порядке:
![\displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7eb454436dc3268ae8d6d2b62f395a7_l3.png "Rendered by QuickLaTeX.com")
Обратите внимание, что если мы изменим порядок сложения матриц, результат останется прежним:
![\displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c1e9cd77bc490913ed30ff63815da355_l3.png "Rendered by QuickLaTeX.com")
- Еще одним свойством сложения матриц является свойство противоположного элемента:
Другими словами, если мы сложим матрицу плюс такую же матрицу, но со всеми ее элементами, изменившими знаки, то результатом будет нулевая матрица:
![\displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-add832e83fe554143cbd4c710315c1c0_l3.png "Rendered by QuickLaTeX.com")
- Сложение матриц также обладает свойством нейтрального элемента:
Это свойство наиболее очевидное, оно означает, что любая матрица плюс матрица, полная нулей, эквивалентна одной и той же матрице:
![\displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac7b0ba246075c196188798be2c6a034_l3.png "Rendered by QuickLaTeX.com")
- Сложение матриц обладает ассоциативным свойством:
Следовательно, порядок добавления матриц тот же. Посмотрите на следующий пример, где мы добавляем 3 матрицы в разном порядке, и результат тот же:
![\displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bae8e10bca43351f3a84f83bfe50ab55_l3.png "Rendered by QuickLaTeX.com")
![\begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2cc2b7a14cacc7e403cd729cd863d309_l3.png "Rendered by QuickLaTeX.com")
![\begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab1f88e74b139451eccb0471988c3db_l3.png "Rendered by QuickLaTeX.com")