Сингулярная или вырожденная матрица

На этой странице вы увидите, что означает сингулярность или вырожденность матрицы. Кроме того, мы покажем вам несколько примеров, чтобы у вас не осталось сомнений, и, наконец, объясним все свойства этого типа матриц.

Что такое сингулярная или вырожденная матрица?

Определение сингулярной матрицы, также называемой вырожденной матрицей, выглядит следующим образом:

Сингулярная или вырожденная матрица — это квадратная матрица, которую нельзя инвертировать и поэтому ее определитель равен 0.

Таким образом, чтобы узнать , когда матрица сингулярна, просто вычислите ее определитель: если результат равен 0, матрица сингулярна, с другой стороны, если определитель отличен от 0, матрица не сингулярна. .

Если вы хотите узнать больше об обратной матрице, вы можете обратиться к этой странице, где подробно объясняется , как инвертировать матрицу с помощью метода Гаусса . Вы также найдете несколько примеров и упражнений, решаемых шаг за шагом для практики.

С другой стороны, сингулярные матрицы также называются нерегулярными матрицами, потому что они означают прямо противоположное регулярной матрице .

Примеры сингулярных матриц

После того, как мы увидели объяснение сингулярной или вырожденной матрицы, давайте посмотрим несколько примеров сингулярных матриц с несколькими измерениями:

Пример сингулярной матрицы 2 × 2

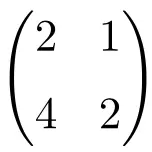
пример сингулярной или вырожденной матрицы размерности 2x2

Мы можем легко убедиться, что это сингулярная матрица, вычислив ее определитель:

$\displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}$

Определитель матрицы 2-го порядка равен 0, значит, это сингулярная матрица.

Пример сингулярной матрицы 3 × 3

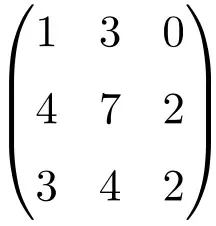
пример сингулярной или вырожденной матрицы размерности 3x3

Мы должны решить определитель матрицы, чтобы убедиться, что это необратимая матрица:

$\displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}$

Определитель матрицы третьего порядка дает 0, следовательно, это сингулярная матрица.

Пример сингулярной матрицы 4 × 4

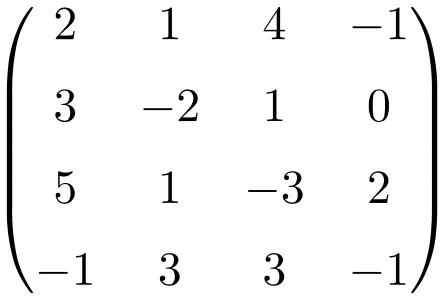
пример сингулярной или вырожденной матрицы размерности 4x4

Составив определитель матрицы, мы покажем, что это сингулярная матрица:

$\displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}$

Определитель матрицы четвертого порядка равен нулю, поэтому ее обратной матрицы не существует.

Внимание: если у вас есть сомнения по поводу расчета определителей, вы можете обратиться к странице , как вычислить определитель .

Свойства сингулярных матриц

Характеристики этого типа матриц следующие:

По крайней мере, два столбца или две строки сингулярной матрицы представляют собой линейные комбинации и, следовательно, являются линейными зависимыми.

Любая матрица, содержащая строку или столбец, заполненные нулями, является сингулярной матрицей.

Ранг сингулярной или вырожденной матрицы меньше ее размера.

Матричное произведение сингулярной матрицы, умноженное на любую другую матрицу, дает еще одну сингулярную матрицу. Это условие можно вывести из свойств определителей:

$\text{det}(AB) = \text{det}(A) \cdot \text{det}(B)=0 \cdot \text{det}(B) = 0$

Аналогично степень сингулярной матрицы равна другой сингулярной матрице независимо от степени, в которую она возведена.

Транспонирование сингулярной матрицы порождает другую сингулярную матрицу, поскольку определитель транспонированной (или транспонированной) матрицы эквивалентен определителю нетранспонированной матрицы:

$\text{det}(A^t) = \text{det}(A)=0$

Умножение сингулярной матрицы на скаляр не меняет ее статуса вырожденной матрицы.

Сопряженный к сингулярной матрице тоже сингулярен.

Треугольные и диагональные матрицы являются вырожденными, если хотя бы один элемент их главной диагонали равен нулю.

Очевидно, что нулевая матрица является сингулярной матрицей.

Точно так же нильпотентная матрица также является сингулярной матрицей.

Система линейных уравнений, связанная с сингулярной матрицей, не имеет решения или имеет бесконечное множество решений.

Наконец, квадратная матрица сингулярна тогда и только тогда, когда она имеет хотя бы одно собственное значение (или собственное значение), равное 0.