Здесь вы узнаете, как вычислить точку симметрии относительно другой точки, относительно прямой и относительно плоскости. Кроме того, вы сможете увидеть примеры и упражнения, решаемые шаг за шагом.
Точка, симметричная другой точке
Прежде чем мы посмотрим, как рассчитывается симметричная точка, давайте рассмотрим, что такое симметричная точка относительно другой точки:
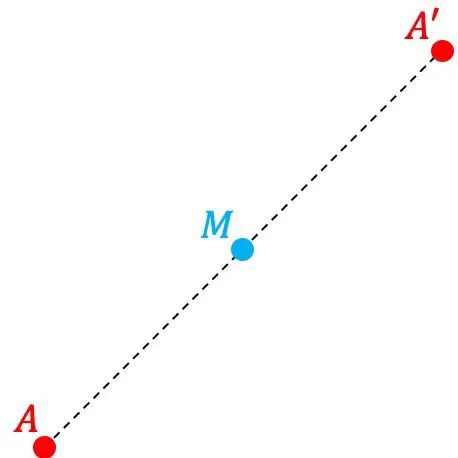
Точка А’ является точкой, симметричной точке А относительно другой точки М, если точка А’ расположена симметрично на том же расстоянии от точки М, что и расстояние между точками А и М. Следовательно, М – это середина отрезка, образованного точки А и А’.
![]()
С другой стороны, мы также говорим, что точка М является центром симметрии.
Итак, для расчета координат точки симметрии воспользуемся формулой середины отрезка :
![]()
Из этого уравнения извлекаем неизвестную точку А’ и получаем формулу для точки, симметричной относительно другой точки:
![]()
Пример нахождения точки, симметричной относительно другой точки
В качестве примера вычислим точку симметрии точки А относительно точки М. Рассмотрим две точки:
![]()
Для определения точки симметрии между этими двумя точками применим формулу точки симметрии относительно другой:
![]()
Теперь заменим точки в формуле:
![]()
И мы работаем:
![]()
![]()
точка, симметричная прямой линии
Мы только что рассмотрели понятие точки, симметричной относительно другой точки. Ну, симметричность точки относительно линии очень похожа:
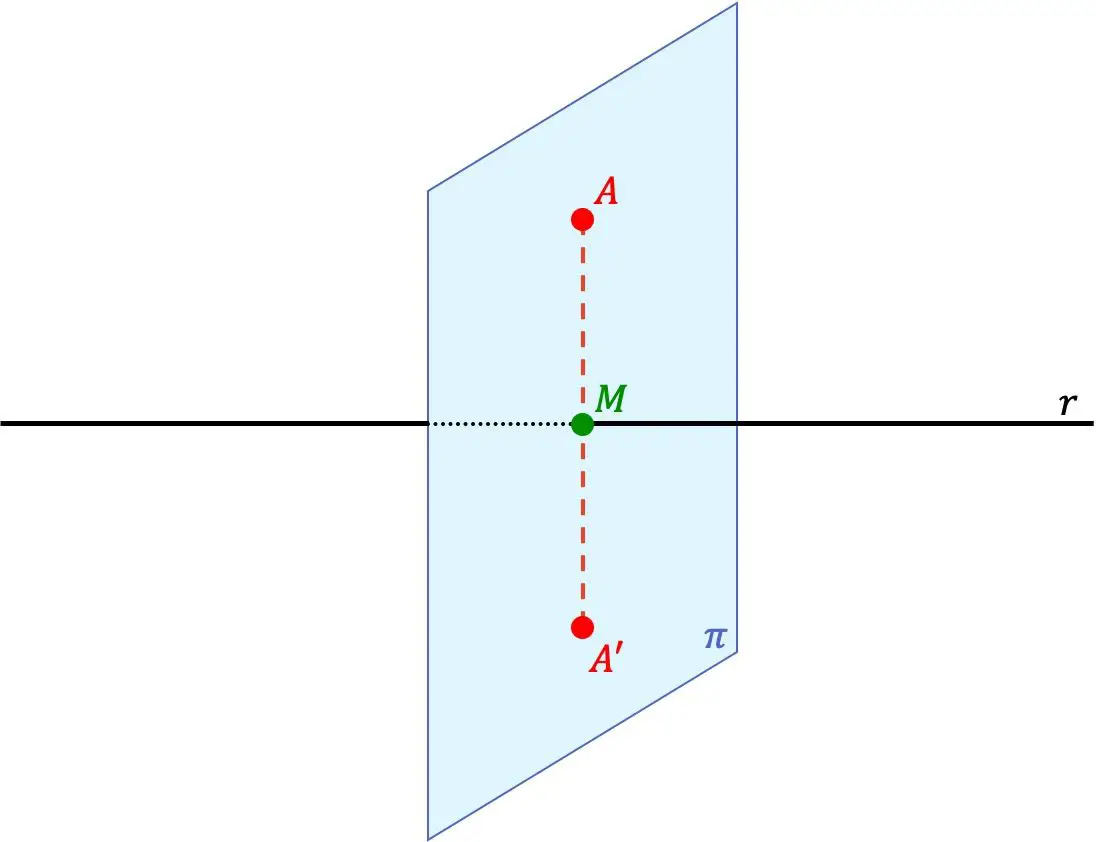
Точка А’ является точкой, симметричной точке А относительно прямой, если две точки А’ и А лежат на одной прямой, перпендикулярной прямой, и при этом расстояние между точкой А’ и прямой равно расстоянию между точкой А и линией.
![]()
Таким образом, линия r также является осью симметрии между точками.
Таким образом, для определения точки симметрии точки А относительно прямой r необходимо выполнить следующую процедуру:
- Находим плоскость, перпендикулярную прямой r , проходящей через точку А (плоскость π предыдущего графического изображения). Для этого мы должны использовать вектор направления линии, который будет вектором нормали к плоскости.
- Вычисляем точку пересечения найденной плоскости и прямой (точка М на предыдущем изображении).
- Мы используем формулу симметричности точки относительно точки (см. раздел выше), чтобы найти симметричную точку точки A относительно точки M. Результатом является симметричная точка, которую мы искали.
Пример расчета точки симметрии относительно прямой
Как только мы узнаем, как вычислить точку симметрии другой точки относительно прямой, мы увидим в качестве примера решенное упражнение:
- Найдите точку, симметричную точке А относительно прямой r. Как говорится, точка и линия:
![Rendered by QuickLaTeX.com \displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5906f8f5fce95109f9f19d93d1f41cd_l3.png)
Сначала нам нужно вычислить плоскость, перпендикулярную прямой r, проходящей через точку А. Вектором, нормальным к этой плоскости, будет вектор направления линии, компонентами которого являются слагаемые перед параметром
![]()
поскольку оно выражается в виде параметрических уравнений:
![]()
А коэффициенты А, В и С уравнения плоскости совпадают с координатами ее вектора нормали, следовательно:
![]()
Точка А должна лежать в этой плоскости, поэтому теперь мы можем подставить точку А в уравнение плоскости, чтобы найти коэффициент D:
![]()
![]()
![]()
![]()
![]()
Итак, уравнение плоскости, перпендикулярной прямой ry, проходящей через точку А, имеет вид:
![]()
Зная уравнение плоскости, нам нужно вычислить точку пересечения плоскости и прямой. Для этого подставляем координаты прямой в уравнение плоскости и решаем полученное уравнение:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd611c8a6c7e516dbb67583b49f0b8e6_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
Теперь заменим значение
![]()
полученное в уравнении линии:
![Rendered by QuickLaTeX.com \displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b0c515e3969169679e810db65a99e3f_l3.png)
Итак, точка пересечения прямой r и перпендикулярной ей плоскости равна:
![]()
Наконец, достаточно найти точку, симметричную точке А относительно точки М; для этого мы можем использовать формулу, представленную в начале этой страницы:
![Rendered by QuickLaTeX.com \begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4b39555d71f045dd42e9422dd077679_l3.png)
точка, симметричная плоскости
Прежде чем рассмотреть метод определения точки симметрии другой точки относительно плоскости, давайте посмотрим, каково ее определение:
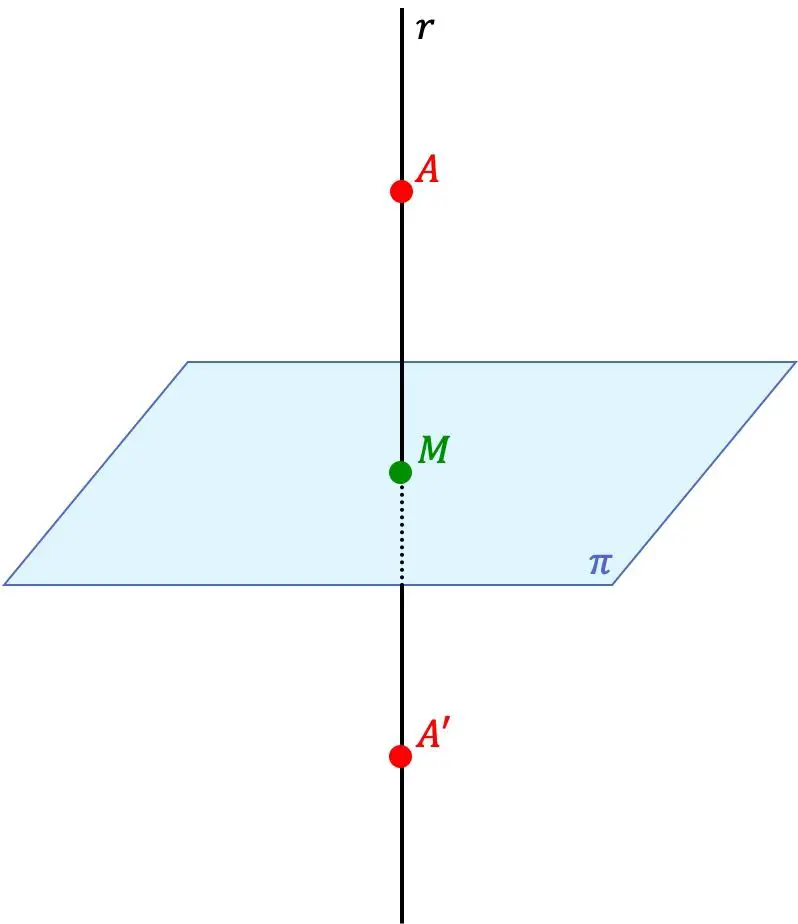
Точка А’ является точкой, симметричной точке А относительно плоскости, если две точки А’ и А лежат на одной прямой, перпендикулярной плоскости, и при этом расстояние между точкой А’ и плоскостью эквивалентно расстоянию между точкой А и плоскостью.
![]()
Таким образом, плоскость также является плоскостью симметрии между двумя точками.
Таким образом, чтобы узнать декартовы координаты симметричной точки А относительно плоскости π, необходимо выполнить следующие шаги:
- Найдем уравнение прямой, перпендикулярной плоскости, проходящей через точку А. Для этого в качестве направляющего вектора прямой будем использовать вектор нормали к плоскости.
- Вычисляем точку пересечения плоскости и найденной прямой (точка М предыдущего изображения).
- Мы используем формулу симметричности точки относительно точки (см. в начале раздела), чтобы найти симметричную точку точки A относительно точки M. Результатом является симметричная точка, которую мы искали.
Пример определения точки симметрии относительно плоскости
Ниже вы можете увидеть решенную задачу относительно точки симметрии другой точки относительно плоскости:
- Определить точку симметрии A относительно плоскости π. Сказав точку и план:
![]()
Первое, что нам нужно сделать, это найти уравнение линии, перпендикулярной плоскости и проходящей через точку А. Для этого мы можем использовать вектор нормали к плоскости в качестве вектора направления линии, компоненты которой X, Y, Z — коэффициенты при слагаемых A, B и C соответственно уравнения плоскости:
![]()
Теперь мы можем построить параметрические уравнения прямой, ортогональной плоскости, с найденным вектором направления и одной из его точек (точки А):
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ec51a68802f626dcd5cf7a3bc1dda59_l3.png)
Зная перпендикуляр, мы вычисляем точку пересечения плоскости и прямой, подставляя координаты прямой в уравнение плоскости:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases} \qquad \qquad \pi : \ 2x+y-z-6=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb4ee2c7f6742eec2e1fa11cac3c5635_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
Теперь заменим значение
![]()
полученное в уравнении линии:
![Rendered by QuickLaTeX.com \displaystyle t=1 \ \longrightarrow \ \begin{cases}x=3 + 2\cdot 1 =5\\[1.7ex] y=-4 +1=-3\\[1.7ex] z=2-1=1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0a9373141f2f699971d5789e1cb0ed0d_l3.png)
Итак, точка пересечения плоскости и перпендикуляра равна:
![]()
Наконец, нам просто нужно найти точку, симметричную точке А относительно точки М. И для этого мы можем использовать формулу, представленную в начале этой страницы:
![Rendered by QuickLaTeX.com \begin{aligned} A' & = 2M - A \\[2ex] &= 2(5,-3,1) - (3,-4,2) \\[2ex] & = (10,-6,2)-(3,-4,2)\\[2ex] & = \bm{(7,-2,0)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e8199cf83bc3bdfbf0a7b2adb65a97af_l3.png)