Свойства определителей

В этом разделе мы увидим, каковы все свойства определителей . Мы также демонстрируем каждое свойство на примере, чтобы вы полностью их поняли. А, кроме того, вы найдете упражнения, связанные со свойствами определителей.

Ниже мы объясним каждое свойство определителей одно за другим, но если вы предпочитаете, вы можете сразу перейти к сводной таблице ниже. 😉

Свойство 1: Определитель транспонированной матрицы

Определитель матрицы эквивалентен определителю ее транспонированной матрицы.

$\lvert A \rvert = \lvert A^t \rvert$

Пример:

$\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}$

Теперь мы транспонируем матрицу 2×2 и находим определитель. Обратите внимание, что мы получаем тот же результат, что и раньше:

$\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}$

Свойство 2: Определитель со строкой или столбцом, заполненными нулями.

Если определитель имеет строку или столбец, заполненные нулями, определитель возвращает 0.

$\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0$

Пример:

$\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}$

В обоих этих примерах определители оцениваются как 0. Поскольку вторая строка первого определителя содержит все нули, а третий столбец второго определителя также содержит все нули.

Свойство 3: Определитель с двумя равными строками или столбцами.

Если определитель имеет две равные или несколько строк или два столбца, определитель равен нулю (0).

Следовательно, если между строками или столбцами существует линейная комбинация, то есть они линейно зависимы, определитель дает 0.

Пример:

$\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0$

В этом случае определитель дает 0, поскольку столбцы 2 и 3 равны.

Свойство 4. Измените строки или столбцы определителя.

Если две строки или два столбца изменяются относительно друг друга, определитель дает тот же результат, но с другим знаком.

$\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}$

Пример:

$\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}$

Теперь меняем порядок столбцов 2 и 3 относительно друг друга. Обратите внимание, что результат тот же, но с другим знаком:

$\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}$

Свойство 5: Умножить строку определителя на скаляр.

Умножение всех элементов во всей строке или столбце на действительное число аналогично умножению результата определителя на это число.

$\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

$\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

Пример:

$\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}$

Теперь мы берем тот же определитель и умножаем всю строку на 2. Вы увидите, что результат будет таким же, как и предыдущий определитель, но умноженный на 2, или 10:

$\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}$

Свойство 6: Определитель матричного произведения

Определитель произведения двух матриц равен произведению определителя каждой матрицы в отдельности.

$\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert$

Пример:

Чтобы продемонстрировать это свойство определителей, вычислим определитель произведения следующих двух матриц двумя возможными способами:

$\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}$

Сначала перемножим две матрицы, затем вычислим определитель полученной матрицы:

$\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}$

Теперь вычисляем определитель каждой матрицы отдельно и затем перемножаем результаты:

$\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}$

Как видите, сначала произведение матрицы, а затем определитель дает тот же результат, что и сначала определение определителя каждой матрицы, а затем умножение результатов.

С другой стороны, это условие не распространяется на операции сложения и вычитания, то есть определитель сложения (или вычитания) двух матриц не дает того же результата, что и сложение (или вычитание) определителей две матрицы отдельно.

Свойство 7: Определитель обратной матрицы

Если матрица обратима, то определитель ее обратной матрицы соответствует обратному определителю исходной матрицы.

$\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}$

Пример:

Мы проверим это свойство, сначала вычислив обратную матрицу, а затем найдя ее определитель. Мы увидим, что результат эквивалентен нахождению определителя исходной матрицы и его обращению.

Поэтому мы инвертируем следующую матрицу и вычисляем ее определитель:

$\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}$

$\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}$

$\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}$

И теперь мы находим определитель исходной матрицы и делаем ее обратную:

$\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2$

$\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}$

Как видите, результаты обеих операций идентичны. Таким образом, свойство доказано.

Свойство 8: Заменить строку определителя

Строку определителя можно заменить сложением (или вычитанием) той же строки плюс (или минус) другой строки, умноженной на число.

Пример:

В следующем примере мы проверим это свойство. Сначала вычислим определитель, затем подействуем на строку определителя и пересчитаем его результат. Вы увидите, как мы получаем один и тот же результат в обоих случаях.

Итак, давайте сначала вычислим определитель 3х3 по правилу Сарруса:

$\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}$

Теперь во вторую строку добавляем первую строку, умноженную на 2:

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}$

А определитель решаем после преобразования одной из его строк:

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}$

В обоих случаях результат был -3. Таким образом, показано, что результат определителя не изменится, если строку заменить суммой той же строки плюс другой строки, умноженной на число.

Свойство 9: Определитель треугольной матрицы

Определителем треугольной матрицы является произведение элементов ее главной диагонали.

Пример:

В качестве примера решим определитель следующей треугольной матрицы:

$\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}$

Свойство 10: Определитель диагональной матрицы

Определитель диагональной матрицы равен произведению элементов ее главной диагонали.

Пример:

В качестве примера возьмем определитель следующей диагональной матрицы:

$\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}$

Сводная таблица свойств определителей

Объясняемые свойства определителей можно резюмировать в следующей таблице:

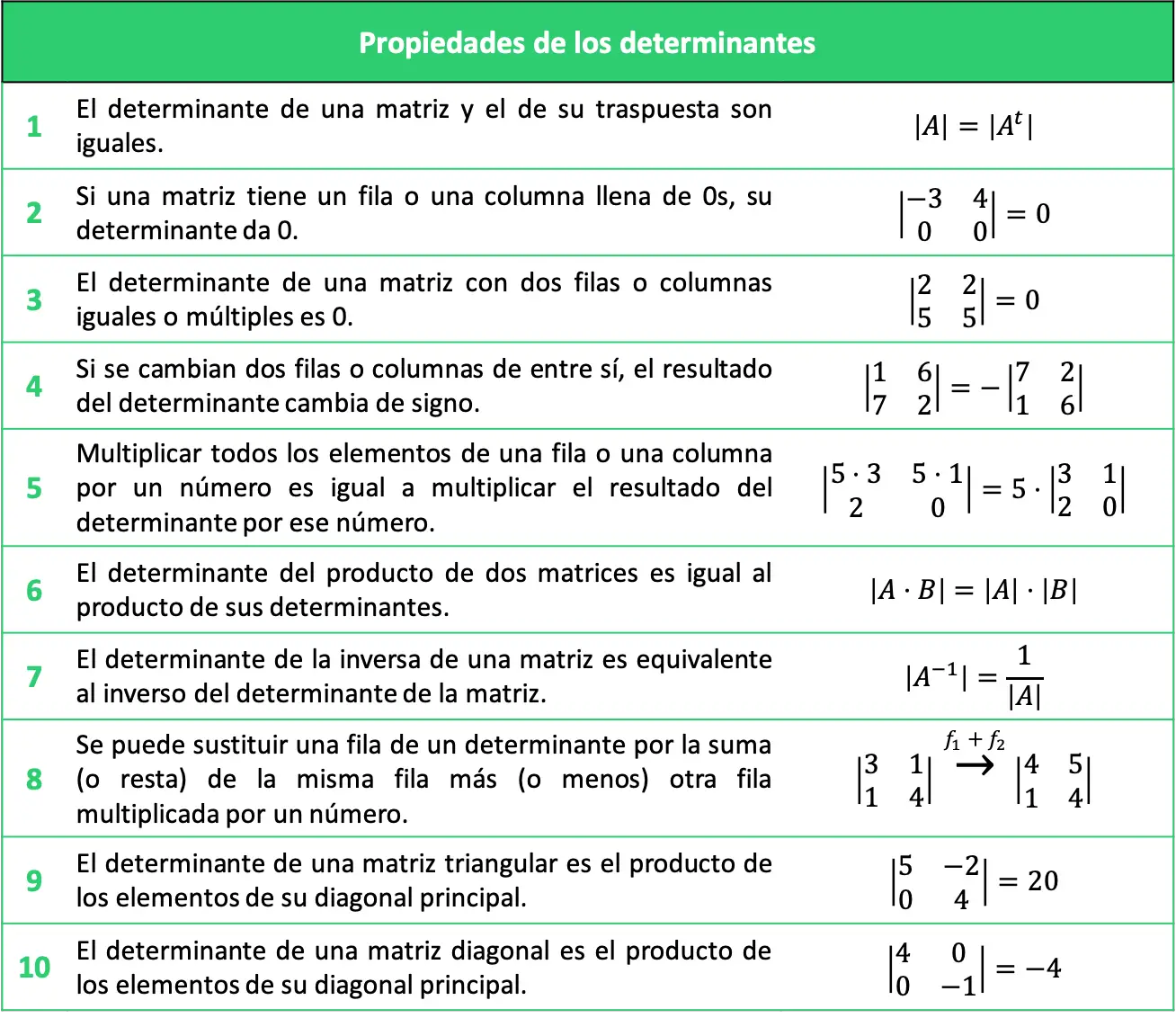
Решенные упражнения со свойствами определителей

Упражнение 1

Решите следующий определитель:

$\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}$

посмотреть решение

Если определитель имеет строку или столбец, заполненные нулями, определитель возвращает 0 (свойство 2). Следовательно, результат определителя равен 0, поскольку третий столбец заполнен нулями.

Упражнение 2

Решите следующий определитель:

$\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}$

посмотреть решение

Если определитель имеет две равные или несколько строк или два столбца, определитель возвращает 0 (свойство 3). Следовательно, результат определителя равен 0, поскольку первая и третья строки равны.

Упражнение 3

Вычислите следующий определитель:

$\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}$

посмотреть решение

Если определитель имеет две равные или несколько строк или два столбца, определитель возвращает 0 (свойство 3). Следовательно, результат определителя равен 0, поскольку четвертый столбец в два раза больше первого столбца.

Упражнение 4

Мы знаем результат определителя, хотя не знаем элементов матрицы:

$\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3$

По результату предыдущего определителя и свойствам определителей вычислите результат следующих определителей:

$\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}$

посмотреть решение

Для)

$\begin{pmatrix} a & c \\ b & d \end{pmatrix}$

транспонированная матрица

$\begin{pmatrix} a & b \\ c & d \end{pmatrix}$

. А определитель матрицы равен определителю ее транспонированной матрицы (свойство 1). Следовательно, результат этого определителя также равен 3.

$\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}$

б) В определении

$\begin{vmatrix} b & a \\ d & c \end{vmatrix}$

столбцы 1 и 2 были изменены относительно определителя оператора

$\begin{vmatrix} a & b \\ c & d \end{vmatrix}$

. Поэтому по свойству 4 результат тот же, что и результат определителя высказывания, но с другим знаком, т. е. -3.

$\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}$

в) В определении

$\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}$

весь второй столбец определителя высказывания умножен на 3. Следовательно, из свойства 5 можно вывести, что его результат также будет результатом определителя высказывания, умноженного на 3, т. е. 9.

$\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}$

Упражнение 5

Мы знаем результат этих двух определителей:

$\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8$

$\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4$

По этой информации рассчитайте:

$\displaystyle \vert A \cdot B \vert$

посмотреть решение

Для вычисления результата определителя не обязательно перемножать матрицы 4х4. Так как определитель произведения двух матриц равен произведению определителя каждой матрицы в отдельности (свойство 6). Еще:

$\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}$

Свойство 1: Определитель транспонированной матрицы

Пример:

Свойство 2: Определитель со строкой или столбцом, заполненными нулями.

Пример:

Свойство 3: Определитель с двумя равными строками или столбцами.

Пример:

Свойство 4. Измените строки или столбцы определителя.

Пример:

Свойство 5: Умножить строку определителя на скаляр.

Пример:

Свойство 6: Определитель матричного произведения

Пример:

Свойство 7: Определитель обратной матрицы

Пример:

Свойство 8: Заменить строку определителя

Пример:

Свойство 9: Определитель треугольной матрицы

Пример:

Свойство 10: Определитель диагональной матрицы

Пример:

Сводная таблица свойств определителей

Решенные упражнения со свойствами определителей

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Оставьте комментарий Отменить ответ