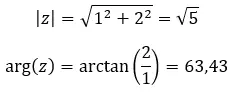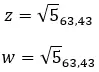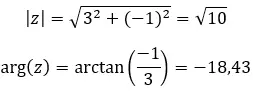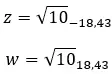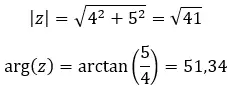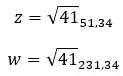В этой статье мы обсудим свойства комплексных чисел , которые могут быть полезны при решении вычислений и упрощении выражений. Перейдем непосредственно к этим свойствам.
Модуль и аргумент комплексного числа
Первое свойство комплексного числа — это модуль и аргумент комплексного числа. Рассчитать очень легко, ведь нужно всего лишь применить несколько формул.
Формула расчета модуля:

Формула для расчета аргумента:

Теперь, если число выражено в полярной или тригонометрической форме, никаких вычислений делать не нужно. Потому что в одном и том же выражении указаны модуль и аргумент.
На изображении ниже вы можете увидеть формулу числа в полярной форме, где |z| – модуль, а α – аргумент.

А на этом другом изображении вы можете увидеть структуру числа, выраженную в тригонометрической форме, где |z| – модуль, а α – аргумент.

равные комплексные числа
Равные комплексные числа — это те, которые имеют общий модуль и аргумент. Итак, из этих двух значений:

Они одинаковы, если соблюдено следующее свойство.
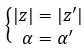
С другой стороны, если у нас есть оба числа в биномиальной форме, мы можем очень быстро и легко проверить, являются ли они двумя равными комплексными числами. Проще говоря, должно выполняться следующее выражение:
а + би = а + би
Давайте посмотрим на примере, определим, равны ли следующие два комплексных числа:
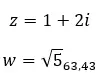
Сопряженные комплексные числа
Теперь перейдем к одному из важнейших свойств комплексных чисел, ведь умение вычислять сопряженное комплексное очень помогает нам в решении сложных делений и упрощениях.
Итак, из этих двух значений:

Мы говорим, что они сопряжены, если они имеют общий модуль и имеют противоположные аргументы. Поэтому необходимо выполнить:
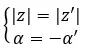
С другой стороны, если у нас есть оба числа в биномиальной форме, мы можем очень быстро и легко проверить, являются ли они двумя комплексно-сопряженными числами. Проще говоря, должно выполняться следующее выражение:
ип + би = ип – би
Давайте посмотрим на примере, определим, сопряжены ли следующие два комплексных числа:
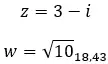
Противоположные комплексные числа
Далее мы переходим к рассмотрению свойств противоположных комплексных чисел. Из этих двух значений:

Мы можем сказать, что они являются противоположностями, если они имеют одинаковый модуль и их аргументы различаются на 180 градусов или π радиан:
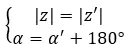
С другой стороны, если у нас есть оба числа в биномиальной форме, мы можем использовать другой, еще более быстрый и простой метод, чтобы выяснить, являются ли они двумя противоположными комплексными числами. Проще говоря, должно выполняться следующее выражение:
а + би = -а – би
Давайте посмотрим на примере, определим, являются ли следующие два комплексных числа противоположными:
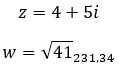
другие объекты недвижимости
Очевидно, что этот набор чисел имеет и другие свойства, такие как обратные комплексные числа и некоторые другие, которые напрямую связаны с основными арифметическими операциями. Хотя обо всем этом рассказывается в других статьях, которые вы можете увидеть в списке ниже.
Узнать о свойствах комплексных чисел
- Комплексные числа
- Операции с комплексными числами
- сложные корни
- Графическое представление комплексных чисел