▷ Теорема об остатке: что это такое, примеры и решенные упражнения ✅

Здесь вы найдете объяснение того, что такое теорема об остатках (или теорема об остатках) и как она применяется к многочленам. Вы также сможете увидеть примеры и, кроме того, попрактиковаться на пошагово решенных упражнениях по теореме об остатках.

Какова теорема об остатках?

В математике теорема об остатках гласит, что остаток от деления любого многочлена P(x) на другой многочлен вида (xa) равен численному значению многочлена P(x) для значения x=a, In другими словами, остаток от деления P(x):(xa) эквивалентен P(a).

Пример теоремы об остатках

Разобравшись с теоремой об остатках, давайте рассмотрим практический пример ее применения:

Вычислите остаток от деления следующих двух многочленов:

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

Чтобы найти остаток (или вычет) от деления многочлена, мы можем воспользоваться теоремой об остатках, потому что в этом случае делящий многочлен имеет форму (ха), то есть он имеет первую степень, коэффициент при переменная x равна 1 и имеет независимый член.

Поэтому мы применяем теорему об остатках, которая гласит, что остаток от такого деления равен численному значению делимого полинома, вычисленного в независимом члене многочлена делителя с измененным знаком, т.е. P (1).

Следовательно, чтобы найти остаток от деления, нам нужно вычислить полином при x=1:

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

Таким образом, остаток деления между полиномами равен 2 .

С другой стороны, мы также можем проверить с помощью правила Руффини деления многочленов , что остаток совпадает с найденным нами результатом:

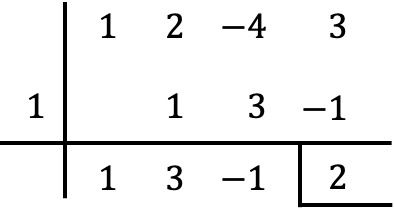
Как видите, с помощью теоремы об остатках определить остаток от деления многочлена на бином гораздо быстрее и проще, чем с помощью правила Руффини, поскольку выполняется гораздо меньше вычислений.

Теорема об остатке и факторах

Из теоремы об остатках и определения корня (или нуля) многочлена мы можем вывести факторную теорему. Итак, из факторной теоремы следует следующее:

Факторная теорема гласит, что многочлен P(x) делится на другой многочлен формы (xa) тогда и только тогда, когда P(a)=0. И в данном случае это означает, что a является корнем или нулем многочлена P(x).

Кроме того, согласно теореме об остатках, это означает, что если многочлен делится на другой многочлен, остаток от этого деления равен нулю, поскольку P(a)=0.

Например, если у нас есть определенный полином:

$P(x)=x^2+2x-8$

Этот многочлен делится на бином (x-2), поскольку P(2)=0:

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

Поскольку x=2 сокращает многочлен P(x), это означает, что x=2 является корнем указанного многочлена.

И далее, поскольку P(2)=0, благодаря теореме об остатках мы можем знать, что остаток от деления

$\cfrac{x^2+2x-8}{x-2}$

равен 0.

Решенные упражнения теоремы об остатках

Чтобы завершить понимание теоремы об остатках, мы подготовили несколько упражнений, решаемых шаг за шагом, чтобы вы могли попрактиковаться. Советуем сначала попробовать упражнение самостоятельно, а потом проверить, правильно ли вы его выполнили.

Упражнение 1

Найдите по теореме об остатках остаток от полиномиального деления

$\cfrac{P(x)}{Q(x)}$

, представляющие собой полиномы, участвующие в операции:

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

Посмотреть решение

Полином делителя состоит только из члена первой степени и независимого члена, причем коэффициент при члене первой степени равен 1. Поэтому мы можем использовать теорему об остатках.

И чтобы применить теорему об остатках, достаточно вычислить делимый полином в независимом члене делителя полинома с измененным знаком, или, другими словами, мы должны вычислить P(2).

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

Таким образом, остаток деления между двумя полиномами равен 21 .

Упражнение 2

Учитывая полином

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

Найдите остаток, полученный в результате деления его на каждый из следующих многочленов:

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

Посмотреть решение

Поскольку все делящие многочлены удовлетворяют условиям теоремы об остатках, мы можем использовать эту теорему для определения остатка каждого деления:

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

Упражнение 3

Посчитайте, сколько должен стоить параметр

$m$

так что остаток от деления многочленов

$\cfrac{P(x)}{Q(x)}$

быть равны 3, причем оба являются полиномами:

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

Посмотреть решение

В данном конкретном случае делящий многочлен состоит из монома первой степени и независимого члена, причем коэффициент при мономе первой степени равен 1. Поэтому мы можем использовать теорему об остатках.

А чтобы использовать теорему об остатках, просто замените независимый член делящего многочлена на смену знака там, где в разделенном многочлене есть x, поэтому мы должны решить P (-3).

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$

Но, очевидно, мы получаем результат, основанный на неизвестном

$m.$

Однако в условии задачи говорится, что остаток должен равняться трем, поэтому мы должны установить найденный остаток равным 3:

$3m-63 = 3$

И, наконец, решаем уравнение:

$3m = 3+63$

$3m = 66$

$m = \cfrac{66}{3}$

$\bm{m = 22}$

Упражнение 4

С помощью теоремы о множителе и остатках определите, является ли полином

$P(x)$

делится на многочлен

$Q(x).$

$P(x) =-2x^3-5x^2-x+2 \qquad \qquad Q(x)=x+2$

Посмотреть решение

Так что полином

$P(x)$

делиться на многочлен

$Q(x)$

деление между этими двумя полиномами должно быть точным, и поэтому остаток должен быть равен нулю.

Тогда, поскольку полином делителя равен

$(x+2),$

По факторной теореме и теореме об остатках мы знаем, что многочлен

$P(x)$

будет делиться на многочлен

$Q(x)$

если он заполнен

$P(-2)=0.$

Поэтому мы должны посмотреть, подтверждается ли это равенство:

$P(-2)=0 \quad \color{blue} \bm{?}$

$\begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}$

Действительно, остальная часть дивизии

$\cfrac{P(x)}{Q(x)}$

равен 0, поэтому многочлен

$P(x)$

Да, он делится на другой многочлен

$Q(x).$

Что вы думаете об объяснении? Тебе понравилось? Будем надеяться! Не забывайте, что вы можете оставить нам свои предложения или вопросы в комментариях. ⬇⬇⬇ Мы вас всех читаем! 😁😁

Теорема об остатке (или вычете)

Какова теорема об остатках?

Пример теоремы об остатках

Теорема об остатке и факторах

Решенные упражнения теоремы об остатках

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Оставьте комментарий Отменить ответ