Простые проценты — наиболее распространенный способ расчета процентов, который используется для самых разных целей: от покупки дома до получения потребительского кредита. Если вам когда-нибудь понадобится рассчитать простые проценты, это руководство покажет вам, как это сделать шаг за шагом. Мы также предоставляем вам онлайн-калькулятор, который облегчит вашу задачу.
Простой процентный калькулятор
Этот онлайн-калькулятор простых процентов представляет собой инструмент, который поможет вам рассчитать любые переменные, участвующие в расчете простых процентов. Чтобы использовать его, просто выберите то, что вы хотите вычислить , и введите данные для запрашиваемых переменных. Затем нужно нажать на кнопку «Рассчитать» и все.
Что такое простой процент?
Простые проценты — это процентная ставка, взимаемая, когда вы инвестируете или одалживаете сумму на определенный период времени. Он рассчитывается путем умножения первоначальной суммы на процентную ставку и время. Таким образом, этот процент используется в постоянных и обычно краткосрочных финансовых действиях.
Поскольку процентная ставка и период времени остаются постоянными, проценты, которые необходимо выплачивать ежемесячно или ежегодно, всегда одинаковы , поскольку проценты не увеличиваются. В этом основное различие между простыми процентами и сложными процентами .
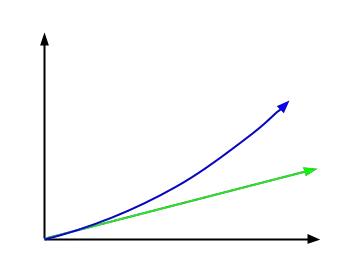
На следующем изображении вы можете увидеть функцию, представляющую простой процент зеленым цветом, и функцию сложных процентов, показанную синим цветом. Как мы видим на изображении, оно имеет гораздо более экспоненциальную форму.
Формула расчета простых процентов
Формула расчета простых процентов: I = C xixt , в которую вмешиваются следующие переменные:
- Первоначальный капитал (C): сумма денег, инвестированная или предоставленная взаймы, на которую рассчитываются простые проценты.
- Процентная ставка (i): этот индикатор сообщает нам в процентах сумму процентов по отношению ко времени. Важно в формуле записать его как можно больше (процентное значение разделить на сто).
- Время (t): продолжительность инвестиционного периода, обычно выражаемая в годах. Хотя ниже мы научим вас переводить его в другие единицы времени, например: месяцы и дни.
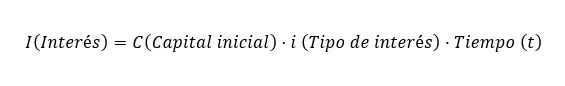
Чтобы увидеть, как используется эта формула, мы можем рассмотреть следующий пример : мы инвестировали 1000 евро по годовой ставке 4%, какой процент мы получим через три года? Чтобы найти полученные проценты, мы должны применить формулу: I = C x (i ÷ 100) xt = 1000 x (4 ÷ 100) x 3 = 120 евро.
Затем из основной формулы мы можем изолировать различные переменные и, таким образом, получить формулы, которые позволяют нам рассчитать начальный капитал, процентную ставку, время и конечный капитал. И это то, что мы увидим в следующих разделах, где мы научим вас рассчитывать эти переменные по формуле, которую вы уже видели, и еще одной очень простой формуле.
Как рассчитывается окончательный капитал?
Чтобы рассчитать окончательный капитал , просто примените логику. Затем, поскольку окончательная сумма равна первоначальной сумме, после того как мы применили проценты, ее формула будет такой: Конечный капитал (Cf) = Начальный капитал (C) + Проценты (I). Это выражение является второй по важности формулой простых процентов после предыдущей.
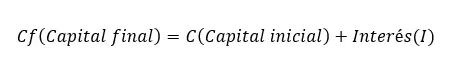
Теперь, когда вы знаете формулу, попробуйте решить этот практический пример: какой окончательный капитал вы получите, если вложите 50 000 евро на 4 года под проценты в 20 000 евро? Просто мы применяем приведенное выше выражение : Конечный капитал (Cf) = Начальный капитал (C) + Проценты (I) = 50 000 + 20 000 = 70 000 евро.
Как рассчитывается первоначальный капитал?
Если мы хотим рассчитать первоначальный капитал, мы можем использовать две формулы, в зависимости от данных, которые они нам предоставляют. Во-первых, мы можем применить выражение из предыдущего раздела, если у нас есть конечный капитал и сумма, генерируемая процентами: Первоначальный капитал (C) = Конечный капитал (Cf) – Проценты (I).
Во-вторых, мы можем выделить стоимость первоначального капитала в простой формуле процентов (той, о которой мы говорили вначале). Таким образом, у нас останется первоначальный капитал (C) = процент (I) ÷ (время (t) x процентная ставка (i)).

Давайте рассмотрим пример второго, более сложного случая: Сколько мне следует инвестировать, чтобы получить проценты на 30 000 евро со ставкой 8% на 2 года? Мы применяем формулу Начальный капитал = I ÷ (tx (i ÷ 100)), в результате чего у нас остается 30 000 ÷ (2 x (8 ÷ 100)) = 187 500 евро начального капитала.
Как рассчитывается процентная ставка?
Чтобы рассчитать процентную ставку , мы также должны использовать простую формулу процента, но изолировать i. Таким образом, у нас остается: Процентная ставка (i) = Процент (I) ÷ (Первоначальный капитал (C) x Время (t)). Как видите, все формулы одинаковы, но выделяют другую переменную.
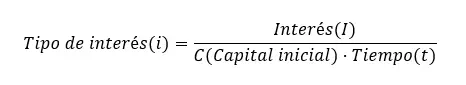
Вот практический пример расчета процентных ставок: по какой процентной ставке нам следует инвестировать 180 000 евро на 5 лет, если мы хотим конвертировать их в 200 000 евро? В этом примере сначала необходимо найти проценты: I = Cf – C = 200 000 – 180 000 = 20 000 евро. А затем решаем: Процентная ставка = 20 000 ÷ (180 000 х 5) = 0,022 х 100 = 2,2%.
Как рассчитывается время?
Наконец, мы можем вычислить время , которое также можно получить из исходной формулы: Время (t) = Процент (I) ÷ (Первоначальная сумма (C) x Процентная ставка (i)). Важно помнить, что формула требует, чтобы единицей времени были годы. Однако если вы хотите выразить ее в других единицах, вы можете использовать следующие варианты формулы:
- I = C · (i / 100) · t, если t — годы (общая формула)
- I = C · (i / 1200) · t, если t — месяцы (Результат в месяцах)
- I = C · (i / 36000) · t, если t — дни (Результат в днях)
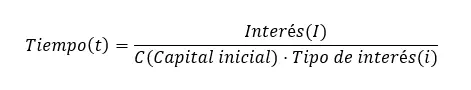
Посмотрите на следующий пример: сколько времени должно пройти, если мы хотим, чтобы инвестиции в размере 40 000 евро принесли проценты в размере 5 000 евро со ставкой 5%? Расчет остается: Время = 5000 ÷ (40 000 х 5 ÷ 100) = 2,5 года. Однако, если мы хотим посчитать его в месяцах, мы можем сделать следующее: Время = 5000 ÷ (40 000 x 5 ÷ 1200) = 30 месяцев.
Реальный пример простого расчета процентов
Теперь вы увидели пример расчета каждой переменной, составляющей формулу простых процентов. Однако мы хотим показать вам последний пример наиболее распространенного расчета , который сам по себе представляет интерес. При применении первой формулы у вас останутся остатки. Если вы хотите просмотреть расчет, вот пример:
Мы занимаем 10 000 евро для инвестиций и хотим подсчитать, сколько денег нам придется выплатить через 5 лет, если с нас попросят 3% годовых. Расчет будет таким:
10 000 х 0,03 = 300
300 х 5 лет = 1500 евро
CF = 10 000 евро + 1 500 евро = 11 500 евро
Таким образом, в конце 5 лет проценты составят 1500 евро, а окончательный капитал, подлежащий выплате , составит 11 500 евро .
заключение
Таким образом, для расчета простых процентов необходимо учитывать сумму кредита, процентную ставку и продолжительность. Далее вы просто умножаете эти три числа, чтобы получить общую сумму выплачиваемых процентов. И если вы хотите вычислить одну из других переменных вместо процентов, вам просто нужно изолировать это значение в общей формуле.